O Calendário é seguramente uma das mais importantes e veneradas aquisições culturais da Humanidade. Tempo qualificado, simbolicamente acentuado, acervo de datas significativas e teoria astronómica simplificada. Segundo E.C. Krupp (A Sky for all Seasons, in: In Search of Ancient Astronomers, Doubleday & Company, 1977: 9): "O ritmo da vida é o ritmo de uma cultura. Este ritmo está vinculado ao ciclo sazonal (...). Um calendário é a expressão da medida da nossa resposta a esses ciclos. É uma ferramenta prática e a aplicação na agricultura é óbvia. Mas a sua verdadeira pertinência vai muito para além disso. É o expediente que possibilita a complexa organização de uma cultura..." (trad. nossa).
O nosso termo "calendário" (Lat. kalendarium) radica em "calenda". As kalendae
(do verbo Gr. καλειν, 'chamar', 'anunciar' [calo, calare], na etimologia mais comum)
assinalavam o primeiro dia dos meses romanos, quando os Pontífices anunciavam o novo mês e instruíam sobre o seu curso (ver). Palavra só se utiliza no plural (pluralia tantum). A contagem dos dias não acumulava, antes "regredindo", contando para trás
(inclusivamente) a
partir das Calendas, das Nonas (5º ou 7º dia dos meses, dependendo de
qual) ou dos Idos (13º ou 15º dia), ver.
Estes dias estariam primitivamente ligados às fases de um calendário
lunar: as Calendas ao aparecimento do primeiro crescente; os Idos marcariam
aproximadamente o meio do mês e o plenilúnio. Todavia, os kalendaria designavam inicialmente registos (regesta, sumários) burocráticos (e.g.,
despesas, empréstimos) que recorressem a qualquer sistema de contagem
(dias, anos, etc.). Aos registos diacrónicos religiosos ou oficiais, os
romanos chamavam Fasti (dies fasti, i.e. "permitidos", em oposição a nefasti). Segundo P. Nothaft (2018: 14, v. bibliografia),
é somente na Idade Média (séc. IX) que o vocábulo se associa
definitivamente ao sistema de contagem que reconhecemos como
"calendário". O calendário litúrgico perpetuará elementos da contagem
pagã do tempo. Se por um lado é marcado pelos ciclos da Páscoa e do
Advento, pela sacralização dos dias do ano através da veneração dos
santos, por outro, a contagem e divisão do tempo herda, na sua
estrutura pragmática, elementos romanos.
Como funciona esta visão intencional do mundo, no nosso caso estruturada em torno do prestigioso Calendário Litúrgico adotado pela Igreja de Roma? Como L. Holford-Strevens resumiu, "...the history of its calculation illustrates many complexities of time-reckoning." (The History of Time: A Very Short Introduction, Oxford University Press, 2005: 44). Os chamados elementos do cômputo (breve introdução e tabelas gregorianas essenciais) permitem determinar as datas das celebrações do calendário e a respetiva organização para qualquer ano. Os elementos foram usados pelos computistas na construção do calendário e na articulação entre o ano litúrgico e o civil. Constitui uma correlação sistemática das observâncias religiosas a partir de uma medição do tempo baseada em fenómenos naturais periódicos: dia solar, mês lunar, estações e ano solar. Emprega-se um conjunto de ciclos cronológicos convencionais tendo em vista evitar a utilização de frações (a que antigamente se chamava "números quebrados") na indicação dos movimentos astronómicos.
Contextualização | Computus Paschalis | Percurso histórico | Luna decimaquarta | Regras | Limites | Ciclos astronómicos | O Ciclo Metónico | Decemnovennalis vs. Lunaris | A Epacta | Lunações intercaladas | Controvérsias históricas | O Computus Medieval | A Letra Dominical | A Indicção Romana | Terminus Paschalis | Páscoa Ortodoxa | A Reforma Gregoriana | A Epacta Gregoriana | Lua Nova Eclesiástica | Ajustamentos ao Cyclus Epactarum
Esta página pode ser resumida como uma abordagem a tópicos relacionados com a determinação da data da Páscoa. Pela sua importância, a determinação e uniformização da data da celebração instituiu historicamente um espaço no currículo, influenciou ou guiou a estrutura de anais e crónicas, promoveu uma atenção particular a determinados ciclos astronómicos. Procura-se um enquadramento do tema, intercalando sucintas resenhas históricas com os aspetos técnicos e exemplificação de procedimentos, numa exposição que não sendo linear nos parece adequada. O núcleo dos conteúdos não se aplica diretamente ao nosso calendário "reformado". É, todavia, importante conhecer este percurso até ao "ajustamento" em vigor, pois somente em perspetiva este pode ser compreendido.
O enfoque é na agilização do chamado computus (método ou "disciplina" que permite a determinação das datas litúrgicas) no calendário em vigor no Ocidente medievo, i.e. o Calendário Juliano (introduzido em 46 a.C. por Iulius Caesar). Convém esclarecer que os calendários Juliano e Alexandrino (é em Alexandria que o cômputo tem as suas raízes) podiam ser considerados "equivalentes". Em todo o caso, para os mais práticos, as tabelas dos chamados elementos do cômputo (acessíveis no menu à esquerda) adequam-se ao calendário reformado (Gregoriano), que hoje utilizamos. Podem ser imediatamente utilizadas para a determinação das datas das chamadas "Festas Móveis".
Procura-se explicar a mecânica deste cômputo, da consagrada implementação medieval no âmbito do Calendário Juliano até à ulterior implementação gregoriana. Note-se que enquanto a primeira é "circular" e "perpétua", na segunda não se verifica a correspondência cíclica entre as variáveis do cômputo. Segundo Arthur Giry, alterou-se a disposição dos elementos cronológicos estabelecida entre o ano solar e o ano lunar e, consequentemente, a metodologia do cômputo (Manuel de Diplomatique, Paris, Librairie Hachette et C.ie, 1894, p.163): "Une conséquence plus importante de la réforme du calendrier fut l’altération des anciennes dispositions des éléments chronologiques dépendant de la coordination établie entre l'année solaire et l’année lunaire, et, conséquemment, la modification des méthodes des anciens computistes pour déterminer la correspondance des phases de la lune avec les quantièmes et en déduire la date de Pâques". Antes, volvido um ciclo solar de 28 anos, os dias da semana repetiam-se na mesma data do mês, ciclicamente. Também o venerável Áureo Número será, na prática, abandonado enquanto expediente para a determinação das datas dos novilúnios, i.e. luas novas. (ibid. pp.163-4). Mas a imprecisão crescente do antigo calendário, com o equinócio gradualmente mais distante da sua data "oficial", há muito reclamava uma "correcção". E esta, por diversas vicissitudes, demorou até ao século XVI e ao pontificado de Gregório XIII
Enquadramento
Nos
primórdios do Cristianismo parece não ter existido sensibilidade para
estas questões, bem pelo contrário: São Paulo escreveu "Guardais dias, meses, tempos e
anos" (Gal. 4, 10), exasperando-se com os que observavam o calendário e os seus dias, considerando que revelavam falta de fé: "Temo que eu
talvez tenha ministrado inutilmente para convosco...",
completou. E São Crisóstomo, no seu comentário
a Coríntios I, vers. 7, dizia algo como: "todo o tempo é festivo para os Cristãos devido à excelência das coisas boas que receberam". Olaf Pedersen (The ecclesiastical calendar and the life of the Church,
in G. V. Coyne, M. A. Hoskin, and O. Pedersen (eds.), "Gregorian Reform
of the Calendar", Pontifica Academica Scientiarum, 1983, 22.) salientou esse desdém pela celebração do calendário e do tempo. Constatou que as cartas de S. Paulo, e outros, contrariamente a toda a tradição epistolar, nem sequer eram datadas. G. J. Witrow (Time in History, Oxford University Press, 1989, p.65) considera que esta situação residia (presumidamente) na crença na iminente "segunda vinda" de Cristo, v. Romanos 13: 11-12.
Primitivamente, existiu decerto uma liturgia da palavra e da celebração eucarística com a esperança na iminente segunda vinda de Cristo, expressa na oração Maranatha - "Vem, Senhor (Jesus)". Todavia uma necessidade litúrgica (a data devia ser antecipadamente conhecida, também pela obrigatoriedade do jejum prévio.) e de afirmação surgirá no período pós-apostólico. Verifica-se uma íntima relação com a contagem Judaica, trazendo contudo novas peculiaridades (e.g., preocupação com a feria, dia da semana, na qual a celebração da Páscoa deveria acontecer: Domingo) bem como, em breve, uma tentativa aguerrida de separação e autonomização relativamente à antiga religião "matricial". Era importante articular a celebração e evitar "heresias" como a controvérsia que surgiu (com notoriedade a partir da segunda metade do séc. II) porque alguns cristãos em Jerusalém e na Ásia Menor observavam a Páscoa no 14º dia do mês judaico de Nisan, data da Pesah judaica, independentemente do dia da semana em que ocorria. O objetivo da celebração era o mesmo mas enquanto os chamados Quartodecimans colocavam o assento na morte redentora, as restantes igrejas privilegiavam a ressurreição. O primeiro Concílio Ecuménico de Niceia (325) colocou termo a esta ambiguidade, optando pela celebração dominical.Também era considerado "anómalo" celebrar a Ressurreição, que aconteceu depois da Crucificação, antes ou no mesmo dia do sacrifício (judaico) do cordeiro pascal, interpretado como figura profética da Crucificação de Cristo.
A
questão do domingo, "o dia do Sol", revestia-se de enorme importância. O
Mitraísmo (um culto solar) era popular e o "Sol Invictus", proveniente
de Emesa, cujo dia festivo coincidia com o solstício de Inverno,
tornou-se culto oficial, adoptado no Império sob Aureliano em 272. A
designação de Cristo enquanto "Sol da Justiça" e a data da celebração
do Natal estão relacionadas com esta envolvente. Constantino, em 321,
institui o "venerável dia do Sol" como dia de descanso judicial e
urbano. Note-se a afirmação do domingo (Gr. Kyriake hemera, "Dia do Senhor") na Ressurreição (Gr. Anastasismos hemera), enquanto dia da Criação da Luz (no Genesis) e oitavo dia após os seis da Criação e do Shabbat. Início simbólico de uma "nova e mais grandiosa criação". (Adolf Adam, O Ano Litúrgico...,
p.44). A paradoxal expressão "oitavo dia da semana" representa pois a
transcendência, a antecipação da eternidade, um "shabbat" eterno.
(Peter Mazar, "Christian Week", in: Wilde, James A. (ed.), At that Time: Cycles and Seasons in the life of a Christian, Chicago, Liturgy Training Publications, 1989, p.64)
Na mais simples definição, a Páscoa
acontece no primeiro domingo depois da Lua
Cheia que sucede ao Equinócio Vernal. Todo o problema da determinação
da
data se resume à articulação dos dois ciclos fundamentais: o das
lunações (obviamente relacionado com as fases da Lua) e o das estações
do ano (solar). Astronomicamente há uma diferença de 11 dias entre
ambos, diferença contemplada pelo argumento da epacta. Recorreu-se, na melhor implementação, ao
antigo Ciclo Metónico,
que relaciona ambos (simplificando: 235 meses lunares correspondem a 19
anos solares). As imperfeições do Calendário Juliano geraram, ao longo
dos séculos, um desfasamento crescente com as estações do ano. A
constatação esteve na base de críticas mordazes nos quatro últimos
séculos que precedem a correção gregoriana, implementada no séc. XVI.
A
necessidade de ciclos convencionais e do recurso a uma lua nocional
explica-se concretamente pelas debilidades colocadas pela observação do
início dos meses lunares (variável segundo a longitude do local), bem
como da existência de oscilações no equinócio e da descontinuidade
colocada pela existência dos anos bissextos:
"The date of the Jewish
Passover was related to the date of the vernal equinox and to the age
of the moon, initially established by direct observation. One problem
with this arrangement was that the date of Easter could vary with
longitude. The exact time of any astronomical event, such as the moment
that the sun enters the first point of Aries (that is, the vernal
equinox), depends on the local time of the observer. Another problem
arose from the institution of leap days in the Julian calendar; these
caused the date assigned to the vernal equinox to oscillate around the
actual event. To circumvent these difficulties, astronomical
observation had to be abandoned. In its place various cycles of greater
or less accuracy were used to predict the astronomical events. The idea
was to use, instead of the real moon, a notional or theoretical moon
with a well-defined period which matched, at least approximately, the
true synodic period. It would then, if the model were accurate, be
possible to calculate the dates of new and fiall moons. Likewise, a
fictional vernal equinox on some fixed date had to be assumed. These
would enable a date to be calculated for Easter which would be valid
worldwide." (Edward Graham Richards, Mapping Time: The Calendar and Its History, Oxford University Press, 1998, p.348)
Usaram-se, portanto, posições artificiais, nocionais), decerto baseadas em posiçõesmédias do Sol e da Lua e nunca no completo aparato teórico da astronomia Helenística, patente na síntese de Ptolomeu (a Astronomia era "suspeita", pela sua relação íntima com práticas astrológicas).
Para evitar complexidades, frações, décimas e todas as irregularidades astronómicas dos movimentos em causa, o
calendário
eclesiástico utiliza expedientes facilitadores, pois nenhum
dos períodos astronómicos na base possui um número inteiro de dias (imediatamente relacionáveis):
1 ano tropical médio = 365,2422 dias solares médios.
1 mês sinódico médio (lunação) = 29,53059 dias solares médios.
365,2422 / 29,53059 = 12,368266 meses.
Na sua forma "defiinitiva", que
durará até à reforma do calendário, os procedimentos do cômputo respeitam as seguintes convenções:
- O Equinócio Vernal (início da Primavera no Hemisfério Norte) é fixado no dia 21 de março, enquanto o aparente,
astronómico, varia
pelo facto de o ano trópico (o das Estações) não ter exactamente 365
dias. No Calendário Juliano, a gradual acumulação dos desfasamentos
desde a época do Concílio de Niceia (325 AD)
fez com que em finais do séc. XVI,
quando se procedeu à reforma do calendário, o equinócio já tivesse
"deslizado" para o dia 11 de março! (Recuava 1 dia em 128 anos, em
média; mas o valor astronómico reconhecido pelas tabelas medievais era imperfeito, e.g., 134 dias segundo as 'Afonsinas'). A importância deste equinócio
"Eclesiástico", para além do simbolismo luminoso e de
renascimento, residia na sua 'regra': o consequente estabelecimento das datas extremas, i.e. intervalo elegível para a celebração; v. limites) impedindo a Lua Cheia Pascal (a primeira depois do equinócio) de ficar aquém dessa data. A data do convencional do Equinócio determinava obviamente osreferidos limites. Se, por exemplo, se usasse 21 de março (o que veio a prevalecer), podia celebrar-se a Páscoa no dia 22 se a luna
xiv caísse no dia 21; todavia quem, no mesmo ano, usasse a data
equinocial de 25 de março (como os romanos apreciavam), precisaria
esperar pela Lua Cheia seguinte (19/20 abril) e celebraria a Páscoa com
uma diferença que ultrapassava um mês relativamente ao primeiro cômputo
mencionado! Isto era bizarro mas aconteceu repetidamente.
- Define-se o conceito de "Lua Nova Eclesiástica" (a primeira Lua Nova
de um mês do calendário lunar esquemático, particularmente a que
antecede a Lua Cheia Pascal Eclesiástica, a primeira da Primavera). É um novilúnio convencional (num calendário preciso
pode diferir até 2 dias do fenómeno astronómico), baseado no Ciclo
Metónico. O conceito desse "novilúnio eclesiástico" teve origem em
Alexandria (na tradição referem-se tabelas de Teophilus sucessivamente estendidas por Cyrillus e
mais tarde adoptadas e ampliadas no seu prazo em Roma por Dionysius
"Exiguus", ratificadas e disseminadas pelo prestígio de Beda, o
Venerável).
- A chamada "Lua Cheia Eclesiástica" acontece sempre no 14º dia, luna decimaquarta, de um mês lunar (de novo, a real ou astronómica pode variar).
- A estrutura do ano lunar eclesiástico (tal como acontece nos
calendários Judaico e Islâmico) arredonda o tamanho dos meses lunares:
os meses lunares passam a ter, convencionalmente, alternadamente 29 ou
30 dias.
- O Ciclo Metónico de 19 anos
é o alicerce do sistema. Um ano lunar eclesiástico comum é composto por
6 meses de 29 dias cada, mais 6 meses de 30 dias cada, totalizando 354
dias; para acertar com o calendário solar, num ano lunar "abundante"
existe um mês intercalar extraordinário de 30 dias, totalizando assim
384 dias. O ciclo de 19 anos deve incluir 12 anos (lunares) comuns e 7
anos (lunares) que incluem mês intercalado, totalizando 6936 dias.
Todavia, 19 anos contém em média 4 dias e 3/4 a mais (por causa dos
bissextos; o bissexto era a repetição do dia 24 de fevereiro, implementada de 4 em 4 anos no desenho do Calendário Juliano: ante diem bis sextum Kalendas Martias), totalizando 6940 dias e 3/4. Uma vez que os 19 anos
(obviamente solares) no Calendário Juliano totalizavam apenas 6939 dias
e 3/4, o movimento da Lua Eclesiástica "saltava" (artificialmente): era
o saltus lunae,
que
acontecia, segundo o expediente que acabou por prevaler, na última lunação do ciclo de 19 anos (a epacta aumentava,
extraordinariamente, 12 unidades [dias] antes do início do ciclo seguinte, acertando ambos os ritmos).
N.B.: a Epacta era o elemento do cômputo que traduzia a diferença entre o ano lunar e o solar. Por "coincidência", era a
idade da Lua, em dias, no dia 22 de março, data que assinalava o
término ou limite mais recuado em que a Páscoa poderia cair (Pascha primum). Segundo Beda: "Sed proprie quae in circulo decennovenali annotatae sunt epactae lunam quota sit in XI Calendas Apriles [22 de março], ubi paschalis est festi principium (...)." (De Temporum Ratione, cap. L).
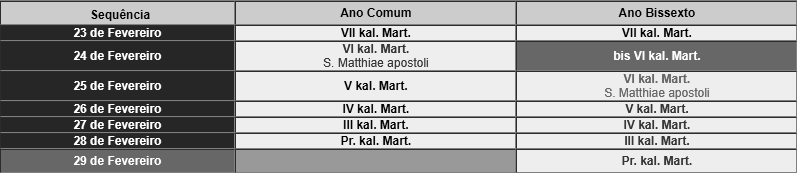
O bissexto: contagem sequencial, ano comum e a inserção do dia extraordinário de
Fevereiro num ano bissexto (com denominações dos dias no sistema
romano). A Festa de S. Matias é considerada "baliza" desde a época
medieval. "Bissexto" significa, de facto, bis sextum, porque se repetia o sexto dia das Calendas de Março.
Descrição do ciclo: a idade da Lua era considerada nulla no
início do ciclo e sofria um incremento de 11 em cada ano. Um mês de 30
dias era teoricamente intercalado no final do ano lunar sempre que a epacta
ultrapassasse 30 no primeiro dia do novo ano (solar). Este procedimento
subtraía 30 unidades à epacta e determinava automaticamente a posição dos sete anos que
continham mês (lunar) intercalar. No final do ciclo a
epacta seria 18 x 11 mod 30 = 18; consequentemente 18 + 11 = 29 no
início do ciclo (Metónico) seguinte. Portanto, se um dia ficar de fora, as epactas
sequentes aumentam 1 unidade. A omissão desse dia é precisamente o mencionado
"saltus lunae", que acerta a contagem. Este esquema permitia conhecer as luas
eclesiásticas a partir da epacta do respectivo ano. Para determinar o dia da semana utilizava-se um sistema de dies concurrentes (número da feria dentro da semana de sete, v. adiante), mais tarde preterido pelo expediente das Letras Dominicais (ou "letras feriais").
Ver infra explicação explicação mais detalhada do funcionamento do ciclo. Note-se que enquanto para os Romanos feria significava um dia de solenidade, na Igreja ela passou a significar um dia comum.
De acordo com a regras acima, as luas eclesiásticas e as datas da
Páscoa eram rigorosamente cíclicas no Calendário Juliano: 7 x 4 X 19 =
532 anos (7 dias da semana; 4 anos do intervalo entre bissextos; 19
anos do Ciclo Metónico). Em 532 anos repetiam-se as datas solares, as
datas lunares e os dias da semana. Era o "Magno Ciclo Pascal". Saliente-se que NÃO há
qualquer ciclo com essa simplicidade no Calendário Gregoriano. O
problema residia na gradual falta de sincronização com as Estações do
Ano. A Reforma de
1582 trouxe ajustamentos importantes, nomeadamente declarando que
três em cada quatro anos centenares serão comuns e não bissextos e
introduzindo um novo Ciclo de Epactas
(a epacta é, no contexto
gregoriano, a idade em dias da Lua Eclesiástica no dia 1 de janeiro e o
ciclo contempla correções sistemáticas para os diferentes intervalos
cronológicos). Foi necessário, como se sabe, omitir 10 dias do
calendário para o sincronizar com as Estações do Ano (ao dia 4 sucedeu-se o dia 15 de Outubro de 1582; em Portugal
adoptou-se de imediato esta correção).
NB: A utilização de uma era cronológica não era
necessária numa Tabela Pascal. Mas seria cómoda. A primeira utilização
conhecida da chamada Era Cristã (domini nostri Iesu Christi) surge na tabela de Dionísio "Exiguus" que percorre os anos de 532 a 626. O início em 532 AD
foi uma coincidência. A utilização da Era de Diocleciano foi até então
predominante nas tabelas (era usada pelos Alexandrinos) e a mudança estender-se-á, lenta e gradualmente.
Dionysius
parece ter-se respaldado em algumas "coincidências": 23 de Março de 532
foi a data do equinócio vernal e um novilúnio, razões para colocar a
data no início de um ciclo; estudando em retrospectiva, verificou que a
primeira lua nova de 325, o ano do Concílio de niceia, caiu no 1º dia
de Janeiro; finalmente, 1 a.C. (o ano em que acreditava que Cristo
teria nascido) também estava, nesta sequência, no início de um ciclo.
Deste modo, concluiu que o primeiro "magno ciclo" (victoriano) de 532
anos começara em 1 a.C e o seguinte em 532. Consequentemente, inventou
uma nova era com início no seu ano 1 (1 A.D.), evitando a associação do
Cristianismo com a o cômputo dos anos de Diocleciano, então utilizado
pelos alexandrinos. O seu método foi gradualmente adoptado. Isidoro de
Hispalis (Sevilha) estendeu as suas tabelas pascais por mais 95 anos e
Beda, finalmente, completou-as até abrangerem o período completo de 532
anos, a partir do qual as datas se repetem).
Primórdios
Escrutinando os nebulosos primórdios do cômputo (e acautelando a eventual
escassez de evidências e a diversidade das opiniões académicas), o
primeiro período a ser
utilizado na mencionada correlação lunissolar parece ter sido o octaeteris
(no qual 8 anos equivalem aproximadamente a 99 meses), todavia perdendo
1 dia e meio ao longo do ciclo. Hippolytos (séc. III), em Roma, procura
extrapolar a partir daí através de um ciclo de 112 anos mas os erros acumulam-se. Entretanto,
Augustalis, autor de outro modo desconhecido e com datação debatida,
apresentou no seu Laterculus
("pequena placa" ou "tabela") um novo ciclo no qual
84 anos (Julianos) equivaliam a 1039 meses sinódicos. Era múltiplo do ciclo solar de 28 anos (3 x 28), verdadeiramente cíclico na vertente solar mas menos preciso na lunar.
A partir desta altura, também em Roma já se usava a epacta para ancorar a
"idade" da Lua (todavia referida a 1 de janeiro e com valor inicial 1
(não nulla
como no uso alexandrino). Sobreviveram diversas versões do ciclo de 84
anos, baseado (segundo Alden Mosshammer: The Easter Computus and the Origins of the Christian Era,
Oxford Early Christian Studies, 2008: 204 et seq.)
no ciclo solar de 28 anos (recorrência
dos dias da semana no Calendário Juliano) e numa combinação de quatro
ciclos de 19 anos e um lunar de oito; o "saltus" acontecia no final de
cada 12º ano do ciclo. Tudo se articulava quanto aos dias da semana mas
as datas da Páscoa não formavam uma série. Acresce que Roma persistiu,
por tradição, no uso da data de 25 de março para o Equinócio
Vernal, uma aberração em termos astronómicos (data convencional decerto
recebida de fontes antigas pois adequava-se ao fenómeno no séc. III
a.C. e não no séc. I d.C.). E por volta do séc. III, no período da
génese do cômputo, o Equinócio seria geralmente no dia 21 de março (25 Phamenoth no calendário dos Egípcios), data adoptada em Alexandria. Os romanos
também insistiam em não celebrar a Páscoa depois de 21 de Abril,
garantindo assim que o jejum quaresmal não interferia com a celebração
da Parilia, festival do nascimento da cidade (natalis Urbis),
desde a época Imperial. Mas ainda em relação à data de 25 de março,
refira-se que os escribas anotavam tipicamente ambos os "equinócios": equinoctium secundum Graecos e equinoctium secundum Latinos,
nas respectivas datas dos textos dos calendários (e o mesmo para os
solstícios). As datas cardinais do ano, segundo os Romanos, foram
expendidas por Plínio, um dos autores mais lidos e influentes: 25
de março, 24 de Junho, 24 de Setembro e 25 de Dezembro. De modo geral,
foi a relação com o ano litúrgico e as peripécias da Encarnação de
Cristo (datas referidas eram associadas a momentos fundamentais) que
perpetuaram as referências ao dia 25 de março na literatura, mesmo
depois da aceitação inequívoca do "modo" Grego a partir do século VIII.
(vide Nothaft, 2018: 31)
Em Alexandria, ainda antes do Concílio de Niceia,
adopta-se, como sabemos, o ciclo mais preciso e adequado: o Metónico
(acima descrito). Embora conhecido há
séculos pelos astrónomos, foi aqui usado pela primeira vez neste
contexto, tudo indica, por Anatolius (erudito e futuro Bispo de
Laodiceia). O ciclo englobava 235 lunações, dezanove anos lunares, dos
quais sete seriam embolísmicos (3º, 6º, 8º, 11º, 14º, 17º e o 19º),
seguindo a lógica do gradual desfasamento luni-solar.
Entretanto, o monge Dionysius Exiguus (séc. VI) giza, seguindo a prática alexandrina, uma
série de 95 anos seguindo princípios alexandrinos e nem menciona um
ciclo de 532 anos descoberto aparentemente por acaso e de modo
labiríntico (a partir de elucubrações de cronologia bíblica) por Victorius de Aquitânia, que na opinião de alguns especialistas, e avaliando o que o autor deixou escrito, não retirou a ilação evidente (i.e.
não compreendeu que se tratava do período que consegue relacionar todas
as "variáveis" fundamentais e completar um grande ciclo definitivo, (v. infra).
Outros consideram que decerto terá compreendido esta correlação dos
períodios (19 x
28). É, todavia quase impossível que em Alexandria esta multiplicação
fosse desconhecida; bem pelo contrário. Este período está atestado numa
crónica de Annianus de Alexandria (Gr. Ἀννιανός ὁ Ἀλεξανδρεύς), da qual
alguns fragmentos nos foram transmitidos por Syncellus no séc. IX (v. Nothaft, P., Scandalous Error - Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford/New York, Oxford University Press, 2018: 47). Em qualquer caso, o sistema "victoriano" permitia muitas
"irregularidades" nos resultados e os métodos estritamente
alexandrinos e supostamente "nicenos" de Dionysius prevaleceram. Beda (o Venerabilis)
será o grande organizador e divulgador da "disciplina" e da sua metodologia. Seguirá
os princípios de Dionysius, simultaneamente valorizando a relação 19 x
28 = 532 (que multiplica o ciclo decemnovennalis
(19) pelo ciclo solar (7 x 4 = 28) no qual as datas recorrem no mesmo
dia da semana), deste modo apresentando uma Tabela Pascal Perpétua, de cyclo magno paschae, de 532 anos (o tal número), no final dos quais tudo se repete (como o erudito beneditino salientou).
Contextualização, os textos do cômputo
O que é o tempo para a computística? Segundo o autor anónimo do chamado "Cômputo de Munique" é o intervalo que medeia entre o princípio e o fim: "Tempus, quid est? Tempus est spatium tendens de principio usque in finem" (Munich Computus 1, ed. and tr. I. Warntjes, The Munich Computus: Text and Translation, Irish Computistics Between Isidore of Seville and the Venerable Bede and Its Reception in Carolingian Times, Stuttgart 2010: 2–3)
Como T. E. R. Philips resumiu ("The Calendar", in: Hutchinson's Splendour of the Heaven (vol.2), Hutchinson & Co., 1923, p.808), os calendários adoptados pertencem, em geral, a um de três tipos principais: exclusivamente solares, exclusivamente lunares ou lunissolares. No primeiro, o referente é o ano e a duração dos meses é arbitrária, convencional e sem relação com as fases da Lua; no segundo tipo, puramente lunar, a duração do mês é entendida como fundamental e o ano consiste basicamente em doze lunações ou 354 dias, sem qualquer relação com as estações do ano; no terceiro caso, lunissolar, o ano habitualmente consiste em doze lunações, sendo os meses (convencionalmente) constituídos alternadamente por 29 e 30 dias, eventualmente inserindo um mês intercalar para compatibilizar o calendário (aproximadamente) com as estações do ano. O primeiro tipo pode ser exemplificado pelo Calendário Juliano (que com pequenas modificações é praticamente equivalente ao nosso, actual), o segundo pelo Calendário Islâmico (que se guia exclusivamente pela Lua, sem intercalações, i.e. os meses são independentes das estações do ano), o terceiro pelo Calendário Judaico (que utiliza meses lunares mas articula sazonalmente as suas celebrações fundamentais).
Seria um truísmo assinalar a importância da determinação da data da Páscoa (Pesah em hebreu, Pashã no aramaico falado na Palestina romana, Πάσχα em grego) e da consequente relevância do cômputo incumbente. A data depende do calendário que subjaz e dos termos do cômputo utilizado. Daí as "discrepâncias" históricas e hodiernas, por exemplo com as datas da Páscoa Ortodoxa (cujo cômputo ainda utiliza o Calendário Juliano). As controvérsias e a complexidade inerente testemunham a sua importância. Recentemente, a necessidade de encontrar uma data normalizada e ecuménica para a celebração da Páscoa foi enfatizada em 2015 pelo Papa Francisco (fonte: Agência Ecclesia, 12 de junho de 2015, notícia, arquivada do original), que confirmou a disponibilidade da Igreja para abdicar do método romano atual, favorecendo a unidade Cristã na celebração. A controvérsia continua.
Lutero, algo intempestivo, exprimia o seu descontentamento com as variações da data da Páscoa: "Muitíssimo melhor houvera sido se eles deixassem morrer a lei de Moisés acerca da festa da Páscoa e não conservassem nada da roupa velha...", aconselhando a fixação segundo o curso do Sol. (cit. in Adam, O Ano Litúrgico, Op. cit., p.62). Desde S. Paulo que a antiga lei cerimonial vetero-testamentária se considerava 'ab-rogada', ultrapassada (Cl. 2, 16; 2,20).
Todavia, "mexer" com coisas do calendário é sempre perigoso:
"Tampering with the way we keep
time is perilous. Just listen to the gripes that surface every time we
need to change clocks to accommodate daylight saving time. Listen
carefully to the way some complaints are worded. Some people think that
we’re actually adjusting the sun, not just our clocks. It may be a
comic revelation of the profound belief that most people have that only
God is the keeper of time." (Peter Mazar, "Christian Week", in: Wilde, J. (ed.), At that Time..., Op. cit., p.56)
Antecedentes
Para a compreensão do Calendário Eclesiástico precisamos recuar até à celebração da Páscoa Hebraica (Pesah, Pêssach), a “Festa da Libertação”. Esta acontece sempre no 14º dia do mês Nîsân
(nome que já denuncia a determinante influência da terminologia
babilónica), correspondendo a março/abril, o primeiro do calendário
religioso mosaico (referido por exemplo em Ne. 2,1 ou Est. 3,7). Também é chamado Aviv (ou Abib), designação equivalendo, na prática, a "Primavera" ou "Tempo da Primavera".

Dt. 16,1, in Del Rio, Compendio Metodico Y Claro Del Cómputo Eclesiástico Antiguo Y Moderno. Madrid, 1790
Todavia, a contagem dos anos continua a ser feita a partir do sétimo mês, Tishri, o antigo começo do ano religioso (prévio à influência babilónica), após o novilúnio que sucede ao equinócio outunal, quando se celebra o novo ano, Rosh Hashanah (Adam, A., The Liturgical Year, Collegeville, MN, The Liturgical Press, 1990: 6, 12). Esta festividade é relacionável com o "Yom Teru'ah" bíblico.
Acontecendo no 14º dia de um mês lunar, a Pesah coincide sempre com uma lua cheia (i.e., com 14 dias de “idade”), a primeira após o equinócio que marca o início da primavera no hemisfério norte, podendo ocorrer obviamente em qualquer dos dias da semana (e não necessariamente a um domingo). Segundo o Evangelho de S. João, a Crucificação aconteceu neste 14º dia. Esta interpretação é simbolicamente validada porque Jesus é considerado o novo Cordeiro Pascal, pois fora assim que João Baptista O apresentara aos seus discípulos: "Eis o Cordeiro de Deus que tira o pecado do mundo" (Jo. 1,29). A Páscoa foi naturalmente associada ao equinócio vernal, triunfo da luz sobre as trevas, na qual Cristo, "Sol de Justiça", se elevou e brilhou. A celebração era um retorno ao tempo salvífico.

Como veremos, agiliza-se a autonomia (afirmação e independência relativamente à "Sinagoga", preocupação por vezes muito áspera nos primórdios, e.g., Eusebius, Vita Constantini, Lib. iii., 18-20; excerto relevante, algo polémico, tradução inglesa de Averil Cameron e Stuart Hall, Clarendon Ancient History Series, Oxford, 1999), antecipação (prognose das celebrações na estrutura da liturgia) e uniformização (normalizando e estabelecendo procedimentos "universais").
O
Cristianismo, afastando-se deliberadamente da sua matriz Judaica,
adapta o simbolismo solar e luminoso (e.g., o Domingo, o dia do Sol)
dos romanos, bem como as suas instituições, direito e iconografia
(e.g., o halo ou nimbus dos
cultos pagãos, a pose imperial de Cristo). Tertuliano (Tertullianus,
c.160-c.220), nascido em Cartago, na África Proconsular, havia negado
as conotações solares mas Eusebius de Cesareia, na época de
Constantino, realçou que o "Dia do Salvador" é assim nomeado pela sua
relação com a Luz, i.e. o Sol. Mas enquanto Constantino (com motivações
"honestas" ou não) se equiparou ao Sol (ou mesmo, provavelmente, a
Cristo), Deus é, para Eusebius, transcendente, um Criador separado da
Natureza, não é parte dela como no Platonismo (para o qual o Cosmos é
uma "criatura viva", onde o Sol, a Lua e os planetas e tudo o resto são
entidades que participam do divino). Todavia, no Judaísmo, Deus era
transcendente, fora do Mundo ("O Céu é o meu Trono...", Is 66:1), que
criou ex-nihilo. Santo
Agostinho, apesar do seu respeito e afinidade com o Platonismo, também
refutou a doutrina que este expendia da equivalência Deus-Universo.
O cômputo em contexto
O computus será um tipo de texto ou toda uma disciplina dedicada ao calendário, mormente aos ciclos solares e lunares, bem como à contagem do tempo. Segundo Faith Wallis, na sua introdução ao De temporum ratione de Beda (influente teólogo, historiador e cronologista, falecido em 735), não se trata de uma ciência observacional ou de uma física do tempo, mas de uma técnica que padroniza o tempo em ciclos repetidos segundo determinados princípios convencionais (1999: xx, ver bibliografia). Traduz-se numa representação do cosmos que é, concomitantemente, matemática e teológica (Stevens, Wesley, “Rabani Mogontiacensis Episcopi De computo”, Corpus christianorum. Continuatio mediaevalis 44, Turnholti: Brepols, 1979: 167). Número e computus estavam no cerne do entendimento da Natureza. De facto, Numerus ou Ratio numerorum são investidos de importância metafísica: "...Tu, porém, regulaste tudo com medida, número e peso" (Sb. 11, 20). "A computação, não a observação, governava a problemática da determinação da data da Páscoa, uma problemática que, no século VIII se tornou nuclear no ensino medievo acerca do mundo natural." (McCluskey, S. C., Natural Knowledge in the Early Middle Ages, in: Lindberg, D. e Shank, M. (Eds.), The Cambridge History of Science, Vol 2, 2013, p.294 [trad. nossa]).
Um dos expedientes tradicionais de exposição cómoda e estruturada da informação é a utilização de tabelas, relacionação de "parâmetros" do cômputo verificável nos livros litúrgicos, como o Missale Romanum ou o Kalendarium. J. Chabás e B. R. Goldstein, na introdução aos Essays on Medieval Computational Astronomy (Leiden, BRILL, 2015), argumentam que ao longo da Idade Média (e até ao limiar da era moderna), as tabelas constituiram o expediente mais bem sucedido e económico de disponibilização de informação acerca de procedimentos matemáticos e modelos astronómicos, facilitando os cálculos associados. Uma das principais razões terá sido a inexistência de um sistema de notação adequado para a representação dos algoritmos utilizados [v. orig.].
Transportando consigo grande parte da elenco do Quadrivium, o cômputo também ocupou um lugar relevante no âmbito da chamada doctrina christiana na Europa Carolíngia (Wallis, in Koetsier, T., Bergmans, L. (Eds.), Mathematics and the Divine: A Historical Study, Amsterdam, Elsevier, 2005: 196), a abordagem previamente esboçada por Santo Agostinho (Augustinus Hipponensis) e outros, exortando à reformulação e interpretação da antiga erudição e saberes de modo a servir o projeto do Cristianismo (Wallis, 1999, xxi-xxii).
Os textos historicamente elencados são férteis em missivas e prólogos explicando métodos rivais ou complementares de cálculo. O género proliferará através de fórmulas textuais (argumenta), tabelas, tratados, notas breves (lectiones), mnemónicas e ainda através do chamado computus manualis ou chirometralis, descrito por Beda (Wallis, 1999: 343 et seq.). Acerca deste, o comentário de Wallis refere, com propriedade, que a numeração romana em uso não se adequaria aos processos aritméticos (não permitindo facilmente o cálculo a partir da justaposição visual das respetivas notações numéricas), determinando a pertinência desta metodologia ou, alternativamente, da utilização do sistema grego de equivalência letras-numerais (Op cit., 254-255). Somente em 1202 assistimos à divulgação da chamada "numeração árabe" (os chamados ghubãr, (lit. "poeira", numerais arábicos no Ocidente (Maghrib e al-Andalus, curiosamente revelando diferenças relativamente aos usados no Oriente), o modus indorum no Liber Abaci de Fibonacci. Wallis acrescenta que nenhuma fonte revela concretamente o modo como se calculava (Op. cit., 258), existindo decerto automatismos, rotinas e a possibilidade do recurso a tabelas (e.g., de multiplicação) para operações mais onerosas.
Segundo C. Philipp E. Nothaft (Medieval Europe’s satanic ciphers: on the genesis of a modern myth; British Journal for the History of Mathematics, 2020 (DOI: 10.1080/26375451.2020.1726050), a partir do seu desenvolvimento na Índia e chegados ao Oriente Próximo (a primeira referência em Siríaco data de c.662), os numerais, de 1 a 9 surgem atestados pela primeira vez no contexto Latino num manuscrito do mosteiro de Martín de Albeda (La Rioja), datado de 976. Textos e ilustrações coevas revelam que o conjunto básico era por vezes acompanhado por um décimo "contador", conhecido como "sipos", que parece ter sido utilizado como uma 'casa' reservada. Em algumas fontes é representado por um círculo ou roda. reminiscente do futuro símbolo para o zero. A aritmética baseada nos numerais indo-arábicos chega à Europa Latina na primeira metade do séc. XII, como parte de uma vaga de traduções de obras em Árabe. O texto fundamental, neste âmbito, é o livro (do séc. IX) que descreve o modo de contagem Indiano, de al-Khwarizmi, que conhecerá notável divulgação (N.B.: termo "algorismus" deriva da latinização do nome de al-Khwarizmi). A vaga de textos continua no séc. XIII através de dois manuais extremamente populares: Algorismus vulgaris de Sacrobosco e o Carmen de Algorismo (também conhecido como Algorismus metricus), atribuído a Alexandre de Villedieu. Um segundo género textual através do qual se dará a difusão do sistema a partir do século XIII serão os tratados de aritmética comercial usados nas escolas italianas. O mais conhecido é o Liber abbaci de Leonardo de Pisa (Fibonnaci). com primeira redacção em 1202, a segunda em 1228). O termo arábico para o 'zero' é "sifr", que era habitualmente transliterado como "cifra", daí a nossa palavra actual. O zero era "cifra vel solfra vel nichil..." (cifra ou solfra ou nihil, "nada"). Outro nome, particularmente encontrado em fontes do século XII, é "circulus", presumivelmente inspirado no Árabe "da’ira saghir" ("pequeno círculo"). O sistema é inicialmente adoptado na Astronomia e Astrologia (os dois ramos da ciência das estrelas). Também pelos computistas: Reinher de Paderborn no seu Compotus emendatus e Grosseteste nas suas tabelas numéricas e regras computacionais. Nothaft descarta algumas teorias prevalecentes acerca da resistência ou proibição da utilização dos numerais Indo-Arábicos (nomeadamente do zero como sendo algo demoníaco porque representava o que não existe, o vazio), também relacionado com a magia negra. Explica como não há fundamento histórico para esta narrativa que radica em interpretações espúrias e da imaginação de determinados autores recentes.
Para Scott G. Bruce, a fonte do primeiro capítulo do De Temp rat. de Beda será a Romana computatio, texto anónimo (circa 688), codificando a antiga utilização dos sinais manuais para a representação dos números (Silence and Sign Language in Medieval Monasticism: The Cluniac Tradition c.900-1200, Cambridge/New York, Cambridge University Press, 2007: 57).
Em Beda prevalecerá a ratio temporum, a relação com a astronomia, negando a perene tentação da relação mística com os números. Alguns expedientes utilizavam a mão humana como "calculadora", estabelecendo correspondências envolvendo parâmetros do cômputo (que adiante estudaremos), e.g., o ciclo solar de 28 anos (relacionado com as chamadas "epactas solares" ou anni concurrentes, para a determinação dos dias da semana ou feriae) e as articulações anatómicas disponíveis (28 em ambas as mãos, 3 em cada dedo, tendo o polegar somente duas). Para o cálculo relacionado com o ciclo de 19 anos, relevante para a determinação da Epacta ("idade" da Lua numa determinada data pivotal), utilizavam-se as 5 pontas dos dedos de uma mão adicionadas às 14 articulações da mesma.
Procedimentos deste jaez beneficiarão de um surpreendente percurso, dos argumenta carolíngios até à reforma do calendário no século XVI. Ponderados de modo abrangente, na pletora das suas implementações (tradição clássica da representação de cifras, codificação e comunicação, especulações numéricas e correspondências teológicas), talvez seja tempestivo (acautelando a enorme diversidade das implementações), relacioná-los com o valor simbólico dos números, com a mão como ferramenta de comunicação e pedagógica (associada também à música e à proporção), explicáveis ainda por uma semântica alargada na qual computare significará "contar ou somar com os dedos" (Picón, Francisca del Mar, González-Marrero, José, De computo uel loquela digitorum. Beda y el cómputo digital; Faventia (Publicacions de la Universitat Autònoma de Barcelona); Vol. 28, 1-2, 2006: 115-123). É sintomático que surjam na 'contabilidade' da "Summa Arithmetica..." de Luca Pacioli (1494), utilizados em tratados do século XVI destinados a uma audiência abrangente (e.g., o "Computus ecclesiasticus per digitorum articulos mira facilitate traditus...", editado em 1597 pelo influente Clavius na pedagogia da "sua" reforma do calendário) ou, recolhendo um exemplo luso, no eclético "Thesouro de Prudentes..." do mathematico Gaspar Cardozo de Sequeira (editio princeps: 1612), com serôdias reedições no início de setecentos.
 ____
____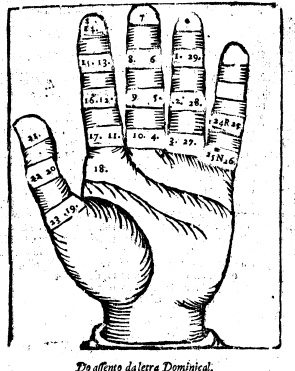
Gravuras relacionadas com a determinação da Epacta e do "assento" da Letra Dominical, respetivamente; Thesouro de Prudentes, Évora, Impressão da Universidade, 1702 (Tratado prymeiro, 4,8)
O computus
traduz o pensamento abstrato medieval sendo dotado de linguagem técnica
e extenso jargão. A literatura típica (antologias com calendário,
listagens e tabelas) inclui duas grelhas incontornáveis: o Calendário
(Juliano) com a estrutura e um qualquer expediente (fórmula ou sistema
de letras-chave) que permita converter a sequência genérica na informação para um determinado ano em particular (fases da lua, dias da semana, nomeadamente os domingos, etc.) geralmente disponibilizando instruções (canones);
a segunda é a Tabela Pascal, cuja informação para um determinado
intervalo de anos é imediata, sendo por vezes acompanhada por argumenta acerca dos parâmetros de cada coluna e textos explicativos (por exemplo as célebres epístolas de Dionysius Exiguus (século VI), defendendo a metodologia e definindo os princípios).
Constituirá, desde a Alta Idade Média, espaço privilegiado para a integração de informação diversa, fragmentos da antiga erudição científica e enciclopédica, parte dela relacionada com os seus alicerces "técnicos", outra relacionada com o calendário por analogia (Wallis, 1999: xxii), da medicina (considerações sazonais e lunares) à prosódia (ritmo e proporções temporais do discurso). Num formato que se revelará perene e popular, estaremos perante a génese do almanaque, atualização e ampliação dos antigos "parapegmata" astro-meteorológicos, encontrados em Plínio, o Velho (Naturalis Historia, Lib. XVIII) ou Columella (De Re Rustica, Lib. XII), sem esquecer "Os Trabalhos e os Dias" de Hesíodo, remoto antecedente relacionável (e.g., vv. 385-617, sobre o calendário agrícola).
Documenta-se, complementarmente, a utilização de diagramas divinatórios (conhecidos desde a época helenística), atribuídos a figuras prestigiosas como Petosiris, Hipócrates, Apuleio ou Pitágoras, e que entraram cedo nas compilações do cômputo. Utilizavam expedientes simples e "mecânicos". Passavam por ponderar numerologicamente as letras do nome da situação/pessoa, incorporar a "idade" da Lua no dia "significativo", a partir daí calcular o remanescente da divisão por 29 ou 30 (mês lunar) e "prever" o desfecho (favorável ou desfavorável), eventualmente em função da posição do número resultante relativamente aos eixos (vertical e horizontal) de um esquema ou diagrama. Podia acrescentar refinamentos, integrando o cálculo da feria (dia da semana), incluir indicação de números favoráveis e nefastos ou personificações da Vita e Mors ("vida" e "morte"). E havia ainda os Lunaria, dedicados à prognose de diversos sucessos, nomeadamente relacionados com a saúde, para cada um dos trinta dias do mês lunar, com antecedentes prováveis no sistema astrológico das mansões lunares.
Uma forma muito persistente de prognosticação nos calendários medievais foi a listagem dos nefastos dies Aegyptiaci (assim designados pelo menos desde o século IV, a referência mais antiga que se conhece recua aos Fausti de Furius Dionysius Philocalus, do ano 354). Os dies atri romanos estavam presentes pelo menos desde a época de Augustus. Supunha-se que os dias "egipcíacos" ou egípcios (habitualmente 24, dois por cada mês), teriam sido sinalizados por veneráveis astrólogos dessa região ou então representavam os dias em que calamidades se haviam abatido sobre o país atravessado pelo Nilo, referência às célebres pragas bíblicas [teoria de Petrus Comestor (1110-1179), teólogo de Troyes]). Chamaram-lhe dies mali, maledicti, ominosi, infortunati ou tenebrosi. A partir do séc. XII também surge a designação Dies Aeger. Surgem nos calendários, ao gosto medievo, em versos "leoninos" (rima interna, entre hemistíquios, i.e. verso latino cujas metades finalizam com rima), e.g. Quarta subit mortem prosternit tertia fortem. Evitavam-se então os empreendimentos e procedimentos médicos, como as purgas. Com o tempo, cada um dos dias foi associado a uma hora dita mala, timenda, aegra ou suspecta (vide Skemer, D., 'Armis Gunfe': Remember Egyptian Days, Traditio, Vol. 65, Fordham University, 2010, pp. 75-106). Eram parte da herança clássica do mundo medieval, tal como a contagem do tempo através do Calendário Juliano. Mas evoluiram autonomamente ao longo dos séculos. Deve referir-se a fluidez e habitual confusão entre diversas listagens disponíveis.
"An important consideration in studying Egyptian days is that they lacked a single universally accepted standard and could thus be remembered differently over time. Days labeled as being Egyptian varied in number from the customary twenty-four to more than fifty per annum, with as many as seven in particular months, and were frequently confounded with unrelated days deemed perilous, ominous, or unhealthy. Treatises on health and diet occasionally juxtaposed warnings about dies aegyptiaci and the unrelated dies caniculares ("dog days"), which constituted a variable range of the hot and unhealthful days of summer, beginning after the helical rising of Sirius, from July 14 and continuing through August until September 4." (ibid, p.79)
Eis uma versão da "perigosa" listagem dos dias literalmente "aziagos" (etimol. lat. aegyptiacus, gr. aiguptiakós, in Dicionário Priberam da Língua Portuguesa [em linha]), segundo mnemónicas versejadas por Sacrobosco (séc. XIII), com as horas mais periclitantes entre parêntesis (fonte: New York Public Library, MA 69, fols. 14r-69v, vide especificamente fol. 26v; referência em Skemer, pp.90-1):
Janeiro 1 (11), 25 (6); Fevereiro 4 (8), 28 (10); Março 1 (1), 28 (2); Abril 10 (1), 20 (11); Maio 3 (6), 25 (10); Junho 10 (18), 16 (4); Julho 13 (12), 22 (11); Agosto 1 (1), 30 (7); Setembro 3 (17), 21 (4); Outubro 3 (5), 22 (9); Novembro 5 (8), 28 (5); Dezembro 7 (1), 22 (6).

O "Ciclo Pascal" é um ciclo lunissolar convencional (relacionando as datas de duas sequências), modificado de modo a permitir a antecipação das datas da Páscoa e incorporando um terceiro ciclo para acomodar a determinação dos dias da semana no calendário solar (porque a celebração maior deverá ser dominical). O chamado ciclo metónico (que consegue relacionar "ciclicamente" uma sequência de dezanove anos solares tropicais com um determinado nº de lunações, v. infra) foi modificado pelos computistas alexandrinos durante o período Patrístico. Quando articulado com outro, o "ciclo solar" (ou "dominical") de 28 anos, nos quais recorrem os dias da semana, resulta um ciclo perpétuo de 532 anos (o “Magno Ciclo Pascal”).
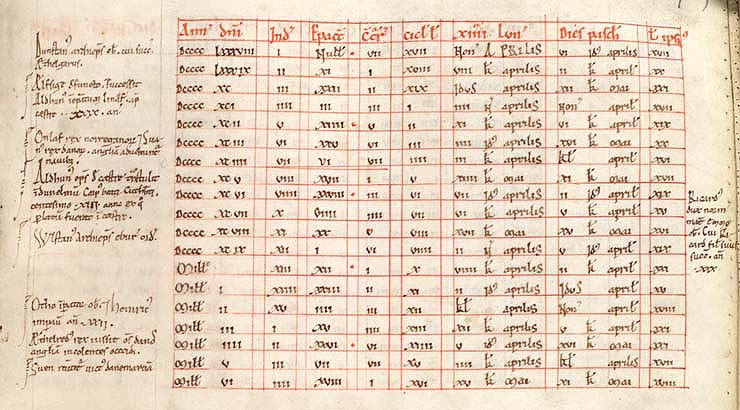
Tabela Pascal (séculos XI-XII), MS 291, f. 140v, Cambridge, Corpus Christi College, Parker Library; CCCC (Parker Medieval Manuscripts Collection). Início em A.D. 1064; Colunas: A.D. | Indicção | Epacta | Concurrentes (dies) | Cyclus Lunae (ou Lunaris) | Terminus Pasch. (data plenilúnio Pascal) | Dies Pasch. (data da Páscoa) | Luna Pasch. ("idade" da Lua no Domingo de Páscoa); as datas são romanas; inscreve ainda a vermelho a indicação dos anos bissextos julianos ("B") e letras dominicais (acrescentadas à última coluna). Note-se que o bissexto eclesiástico é a repetição do dia 24 de Fevereiro e não o dia 29, como no actual uso civil. Ou seja, bissexto é um ano com dois dias VI Kal. Martii. Todavia na prática da Igreja Ortodoxa também á sequencial (dia 29) e celebra-se aí o dia de São Cassiano.
Desde o início do século III, computistae
(computistas) de algumas Igrejas Cristãs, entre as quais Alexandria e
Roma começaram, recorrendo a listagens das fases lunares, a criar
tabelas com sequências de datas para a chamada Lua Cheia Pascal (a que antecede o Domingo de Páscoa) para anos sucessivos, no contexto dos respetivos calendários. O múnus
do computista é, em resumo, prever a "idade" da Lua (em dias), para
determinada data de referência no seu calendário solar, por exemplo o
dia do equinócio, e saber se esta é "elegível" enquanto Lua Cheia
Pascal.
Ao "anexar" um calendário lunar aos calendários solares em uso, os cristãos beneficiaram de uma longa tradição de datação lunar que sobreviveu à instauração destes últimos, bem como da competência babilónica e grega na implementação de ciclos lunares convencionais, sendo o mais conhecido o supramencionado “metónico”, de dezanove anos, enneakaidekaeteris (decemnovennalis, em latim), relacionando satisfatoriamente as lunações com os anos solares. Pode afirmar-se que com a vitória do Cristianismo, o ciclo lunar de 19 anos do calendário Babilónico teve uma inesperada ressurgência através do cômputo Pascal (Neugebauer, O., A History of Ancient Mathematical Astronomy, Springer, 1975, p.621).
Num
episódio relatado por Beda, aquando da aproximação da data final de uma
tabela pascal "dionisíaca" (de 95 anos) em vigor, o abade Ceolfrith (m.
716) assegura numa carta a Nechtan (rei dos Pictos), c. 710, que existe
no contexto das ilhas (Britânicas) o conhecimento para a continuação
desta listagem:
"Quibus termino
adpropinquantibus, tanta hodie calculatorum exuberat copia, ut etiam in
nostris per Brittaniam ecclesiis plures sint, qui mandatis memoriae
ueteribus illis Aegyptiorum argumentis facillime possint in quotlibet
spatia temporum paschales protendere circulos, etiam si ad quingentos
usque et XXX duos uoluerint annos; quibus expletis, omnia quae ad solis
et lunae, mensis et septimanae consequentiam spectant, eodem quo prius
ordine recurrunt." (Aproximando-se do término [a tabela], há
hoje uma abundância de calculadores [computistas] que mesmo nas nossas
igrejas britânicas são vários os que gravaram na memória estas antigas
regras dos Egípcios [i.e. Alexandrinos] e podem facilmente continuar os
ciclos dos tempos pascais por um qualquer número de anos, mesmo até 532
anos, se assim quiserem; depois dos quais tudo o concerne à sucessão do
sol, da lua, do mês e da semana, na mesma ordem de antes eles
recorrem.) (Ecclesiastical History of the English People,
5:21 [trad. nossa]). Por esta altura, a disciplina estava na sua
maturidade. Nos séculos seguintes novas sensibilidades surgirão e as
insuficiências virão à tona.
No final do primeiro milénio, Abão de Fleury (Abbo Floriacensis) refere os ciclos relacionados com o cômputo como circulos quos natura formavit, “ciclos formados pela natureza”. Muito mais tarde, nas cronologias da era moderna, por exemplo nas Exercitationes chronologicae... de Joannes Haiden (editado em Praga em 1761), encontramos a expressão characteres artificiosi para referir o tempo instituído, nomeadamente os cycli annorum, convencionais e dependentes do "arbítrio humano" (p.20). Existindo antecedentes na procura de um computus naturalis (observacional e astronómico, e.g., Hermann de Reichenau, Garlandus "Compotista" ou Walcher de Malvern, no século XI), a abordagem "esquemática" prevalecerá. Mas a passagem dos séculos revelará insuficiências inenarráveis que a Reforma Gregoriana do séc. XVI vai procurar remediar, reconduzindo os ciclos "artificiais" a uma interpretação mais ajustada dos naturais.
Segundo Alden Mosshammer, a primeira utilização adaptada a este cômputo de um sistema de epactas (assinalando a "idade" da Lua em dias para determinada data referencial), deve-se a Demetrius de Alexandria (A.D. 189-232). Esta conclusão é documentada indiretamente (com dificuldades assinaladas pelo especialista) através de fontes coptas e etíopes (mais tardias mas baseadas nas primeiras). Na tradição etíope, o cômputo foi "revelado" a Demetrius (v.g., Ff. 25v-27v, Terefe K., Delamarter, S., Brown, R., Catalogue of the Ethiopic Manuscript Imaging Project: Volume 7: Codices 601-654, The Meseret Sebhat Le-Ab Collection of Mekane Yesus Sseminary, Addis Ababa, Cambridge, James Clarke & Co., 2012). V. ainda Otto Neugebauer (Ethiopic Astronomy and Computus, Osterreichische Akademie der Wissenshaften, Philosophisch-Historische Klasse Sitzungsberichte 347 (Vienna: Osterreichische Akademie der Wissenshaften, 1979), 92-3).
A tabela mais antiga que se conhece, adaptada ao contexto romano, é a de Hippolytus de Roma (século III), abrangendo um período de 16 anos mas sendo decerto estruturada com base no mesmo ciclo de 8 anos, octaeteris (após o qual um novilúnio cai na mesma data do calendário, com uma diferença de mais 1 ou 2 dias), utilizado por Demetrius. Anatolius de Laodiceia terá introduzido no cômputo a utilização do ciclo metónico de dezanove anos (ver), bem como "fixado" o equinócio vernal a 21 de março (25º dia do mês alexandrino Phamenoth). O seu trabalho serviu de modelo às tabelas alexandrinas posteriores (cuja datação se respaldou nos anos da Era de Diocleciano). Por volta do século V, Annianus de Alexandria, coordenando a epacta de Anatolius com o ano civil alexandrino, proporcionou o alicerce para a listagem pascal atribuída a Cyrillus. Esta será utilizada e expandida por Dionysius Exiguus no século VI, notável pela tradução da metodologia alexandrina e influência da sua Tabela Pascal (ver).
Segundo Leofranc Holford-Strevens, na implementação pseudo-Judaica metónica alexandrina, a Lua Cheia Pascal (ver infra) podia situar-se entre o dia do equinócio (25º dia do mês Phamenoth, 21 de março) e o 23º de Pharmouthi (18 de abril). Atendendo a que, por regra, a Páscoa não podia ser celebrada no dia equinocial mas sim a partir do seguinte, o intervalo elegível situar-se-ia entre o 26º dia de Phamenoth e o 30º de Pharmouthi, i.e., entre 22 de março e 25 de abril (The History of Time: A Very Short Introduction, Oxford/New York, Oxford University Press, 2005: 47). Ver explicação para estes limites.
Por
"pseudo-Judaico", Strevens refere-se a um calendário nocional ou
arquetípico, não efetivamente utilizado pelas comunidades judaicas, no
qual não se comprova qualquer preocupação com a determinação da feria (dia da semana) do 1º dia do mês de Tishri.
Seria constituído por doze meses lunares plenos (com 30 dias) e cavos
(incompletos) alternados, cada qual associado ao mês solar no qual
tinha o seu início, como no calendário religioso egípcio (Op cit., 132).
N.B.: A duração dos meses lunares no cômputo é (convém sublinhar) convencional, artificial, um expediente para evitar frações dado que qualquer mês lunar possui de facto 29,5 dias, aproximadamente. Nestes ciclos, para além da normalização e alternância de meses de 30 e 29 dias, recorre-se a intercalações de meses sempre que necessario. As intercalações têm um único objectivo: harmonizar o calendário com as estações do ano. No contexto árabe das origens do Islão, assistiu-se à proibição das intecalações, obrigando à observação astronómica fidedigna do início dos meses (primeiro crescente lunar observável), no contexto de um calendário exclusivamente lunar que, deste modo, não se podia articular com as estações do ano.
Ao contrário do que acontecia em Alexandria, os meses lunares medievais virão a ser vinculados ao mês (solar) no qual termina a lunação. Os meses plenos começam por norma nos meses solares pares (segundo o seu nº de ordem no curso anual) e terminam nos ímpares: impar luna pari, par fiet in impare mense. Pois atendendo à atribuição da lunação ao mês solar em que esta termina, os meses solares ímpares têm lunações plenas, de 30 dias (pares lunae), os meses solares pares têm lunações incompletas ou ímpares, de 29 dias (impares lunae).
Em Alexandria o cômputo pascal foi ajustado ao calendário civil aí usado, reformado na época de Augustus. No Ocidente Latino, os chamados "princípios alexandrinos" são, na realidade, a integração e adaptação (ao Calendaŕio Juliano) de procedimentos e convenções (o recurso ao ciclo metónico, a opção da data do equinócio vernal, etc.), bem como a interpretação que desde o princípio do século VII se consolida empiricamente, associando a epacta anual à "idade" da Lua (em dias) no dia 22 de março (juliano) e, desde o início do VIII, o parâmetro dos anni concurrentes ou dierum concurrentium ordine na literatura medieval do ocidente (que permite conhecer especificamente as feriae, i.e. os dias da semana) ao dia da semana correspondente a 24 de março do ano juliano respetivo. O termo parece ter sido introduzido no léxico computista por Dionysius.
O cômputo alexandrino foi adotado bem cedo na Hispania. Isidoro de Sevilha (599-636), nas Etymologiarum, faz referência às regras nicenas da datação pascal, à proibição da sua contagem a partir do cômputo judaico e alude às tabelas pascais de 95 anos de Cyrillus de Alexandria (c.376-444), das quais uma continuação estaria em uso no seu tempo: "Cujus quidem rationem beatissimus Cyrillus Alexandrinae urbis episcopu in XCV anos per quinquies decem novem calculans, quoto Kal. vel luna debeat paschalis sollemnitas celebrari, summa brevitate notavit. […] Antiquitus Ecclesia pascha quarta decima luna cum Iudaeis celebrabat, quocumque die occurreret. Quem ritum sancti Patres in Nicaena synodo prohibuerunt, constituentes non solum lunam paschalem et mensem inquirere, sed etiam et diem resurrectionis Dominicae observare; et ob hoc pascha a quarta decima luna usque ad vicesimam primam extenderunt, ut dies Dominicus non omitteretur." ("De cyclo paschalis", XVII, 2,-10, in Etymologiarum Libri XX, apud Migne, Jacques-Paul (1859), Patrologia, Cursus Completus, Series Secunda, Tomus VI – Sancti Isidori Hispaliensis, Paris, p. 245).
Assim se resume a relevância da interpretação do legado alexandrino, traduzido por Dionysius Exiguus, sistematizado, explicado e divulgado pelo Venerável Beda, seguindo "deliberações" atribuídas pela tradição ao Concílio de Niceia (que aconteceu no ano que equivalerá, após a adopção do cômputo dos anos de Cristo, a A.D. 325).
"Concílio de Niceia", Hartmann Schedel, Weltchronik [Liber chronicarum] Nürnberg: Anton Koberger, 1493
Em termos concretos, consolidado definitivamente o procedimento, procurava-se a determinação da importante Lua Cheia Pascal. Esta seria no 14º dia (tessareskaidékate, em grego) da lunação (luna xiv, decimaquarta, em Latim, a "quatrozena lua" dos nossos antigos tratadistas) que, em substituição do 14º Nîsân,
faria parte de um sistema de lunações (convencional) constituído por
meses lunares de 29 ou 30 dias fixados no respetivo calendário solar.
Nestes termos, os números ordinais dos dias da lunação são sempre dias
da fase lunar, designando a chamada “idade da Lua” (aetas lunae)
para o dia em causa. As luas eram tão importantes que nos mosteiros medievais a luna do dia era anunciada juntamente com os mártires desse dia na hora prima: o ofício litúrgico matinal.
Por definição, a "idade" na data da Lua Cheia Pascal é sempre 14 (dias), considerando o novilúnio precedente como o seu 1º dia. E o plenilúnio, segundo Beda, "não deve preceder o equinócio, mas segui-lo, como foi ordenado no início da Criação, quando o Sol nasceu no sítio do equinócio (vernal), enquanto a Lua surgiu ao início da noite ocupando o lugar do equinócio outonal" (Wallis, 1999: 131).
Tendo em vista uniformizar e tornar a data independente da longitude do local (o início dos meses lunares depende, tradicionalmente, do primeiro avistamento do "crescente" e a lua cheia astronómica pode até não acontecer concretamente no mesmo dia em dois locais distanciados em longitude), utilizou-se uma “Lua” fictícia ou teorética (dita "Eclesiástica"), bem como uma data também convencional para o equinócio: 21 de março.
A questão da data equinocial era fundamental, pois é o "marcador" do início da estação do ano relevante.
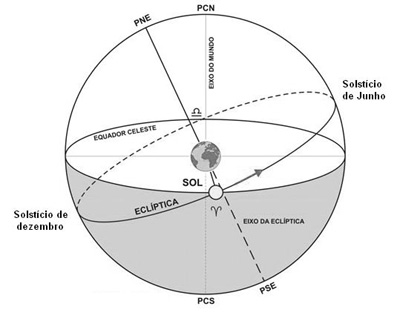
Sol no ponto Áries, equinócio vernal (fonte: I. G. Varella, uranometrianova.pro.br/calenda/glossario.htm)
Pelo
facto de o ano trópico, o período entre duas passagens sucessivas do
Sol (no seu movimento anual aparente) pelo plano do equador celeste não
ser exatamente 365 dias, o momento preciso do equinócio é variável, de
ano para ano, "flutuando" ao longo de um intervalo de dezoito horas
(que não se encaixa necessariamente no mesmo dia. Alexandria
"seguiu" Ptolomeu (i.e.
uma data em consonância com a astronómica coeva) e escolheu a data
equivalente à referida. Roma
persistia no dia 25 de março (convencional desde a instauração do seu
calendário). Queria, no fundo, harmonizar duas tradições. A. Mosshammer
afirmava que era errado atribuir o diferencial entre as datas romanas e
alexandrinas à diferença nas datas do equinócio, pois haveria
flexibilidade e o ciclo utilizado em Roma permitiria que a
celebração recuasse, no limite anterior, ao dia 22: "Although
March 25 was the traditional date of the equinox in the Roman calendar,
the Roman cycle of eighty-four years used in the fourth and fifth
centuries set March 22 as the earliest permissible date for Easter and
thus implicitly accepted the Alexandrian date of March 21 for the
equinox." (The Origins of Feasts, Fasts, and Seasons in Early Christianity (review);
The Catholic Historical Review, Vol. 98, Number 2, April 2012: 337-8). Todavia, diremos que se a escolha em si (nessa épocaj
já não estava isenta de outras complexidades, essa atenção simultânea à tradição da urbe tinha tudo para gerar
"adaptações" e as consequentes dissonâncias com outras Igrejas.
Tecnicamente, a "Lua Cheia Eclesiástica" é, como vimos, o 14º dia de um mês lunar
(podendo diferir da astronómica até um máximo de 2 dias). A regra foi
ainda expandida de modo a que a celebração não coincidisse e
acontecesse depois da celebração judaica. Assim, se o 14º dia de Nîsân fosse a um domingo, a Páscoa seria fixada no domingo seguinte.
«Quae post xiiii. dominica dies occurrit, ipsa est Paschalis dominicae resurrectionis dies» (Beda, De temporum ratione, cap. LIX). A celebraçáo da Páscoa acontece no domingo que se segue ao dia da lua cheia [i.e. com 14 dias de "idade"] pascal)
O problema é conjugar três períodos de tempo não relacionados entre si: o ano solar, a lunatio (lunação, que obedece aos meses lunares) e a semana, pois a celebração deve acontecer sempre num domingo.
Os termos estabelecidos para determinação da data da Páscoa, atribuídos pela tradição ao Concílio de Niceia (onde na verdade somente se estabeleceu a proibição da celebração no 14º de Nîsân, mesmo que este fosse a um domingo, vide Wallis, 1999: xxxvii-xxxviii), determinam:
-
A lunação pascal calculada através do Calendário Juliano é o plenilúnio
(Lua Cheia) que cai no dia 21 de Março ou depois dessa data.
- A Páscoa celebra-se no primeiro domingo posterior ao plenilúnio
pascal. Se este cai num domingo, Páscoa celebra-se no domingo seguinte.
- Do exposto resulta que o o novilúnio (Lua Nova) da lunação relevante
não pode ter lugar antes de dia 8 de Março nem depois de dia 5 de Abril.-
A Lua Cheia será o 14º dia da lunação, contado a partir do novilúnio (Lua Nova Eclesiástica precedente); da data da Lua Nova convencional deverão ter decorrido 13 dias; o aequinoctium (equinócio) é fixado convencionalmente a 21 de março.
Em resumo, a Páscoa deve acontecer no 1º domingo após a Lua Cheia Eclesiástica (13 dias após a Lua Nova Eclesiástica) que ocorre no dia ou após o dia do Equinócio Vernal convencional (21 de março).
Havia, na prática, três interpretações dos limites (intervalo elegível para a celebração):
luna xiv–xx;
luna xv–xxi;
luna xvi–xxii.
A luna xiv é, recordamos, o dia da Lua Cheia (plenilúnio) convencional. Os que advogavam uma das duas últimas opções, afirmavam que o Domingo de Páscoa não podia coincidir com o dia da luna xiv, pois se a celebração começava na noite de sábado/domingo, no seu início ainda estaríamos na luna xiii e, desse modo, a celebração seria precoce, pois adiantava-se à Lua Cheia. Os que defendiam o intervalo xvi-xx acreditavam que a Crucificação acontecera justamente no plenilúnio (luna xiv), logo a Páscoa não podia ser celebrada antes do dia assinalado pela luna xvi. Os oponentes afirmavam que, no limite mais distante, a celebração no dia assinalado pela luna xxii contrariava as Escrituras e o preceito vetero-testamentário relacionado com o período (intimamente ligado à Pesah, equivalendo ao intervalo entre as luas xiv e xxi), no qual os Israelitas apenas poderiam consumir pães ázimos (trata-se da festa dos pães ázimos, Hag ha-matzot, v. Exod 12:15). Em definito, o período xv-xxi será aceite de modo abrangente como estando em conformidade, seguindo a prática Alexandrina. (vide MacCarron, Máirín, Bede and Time: Computus, Theology and History in the Early Medieval World, Routledge, 2020: 3)
Como vimos, a Lua Cheia ocorre no 14º dia a partir do respetivo novilúnio, cujo dia é considerado o 1º da lunação. Logo, o novilúnio pascal nunca acontece mais cedo do que 13 dias antes do dia 21 de março (equinócio convencional). Esta simples subtração permite saber que cai sempre no dia 8 de março ou após esta data.
Na Tabela Juliana Perpétua, verificamos que acontece um novilúnio no dia 8 de março nos anos com o nº de ordem "16" na implementação do Ciclo Metónico (neste ciclo, 235 meses lunares correspondem a 19 anos solares trópicos; configurarão a sequência dos aurei numeri e o nº de ordem de determinado ano, de 1 a 19, será chamado o seu Áureo Número). Nesta mesma tabela, avançando a partir desta data ao longo dos meses relevantes de março e abril, esgotando os números dos restantes dezoito anos do ciclo, verificamos que a última Lua Nova Pascal acontece no 8º ano da série (Áureo Número = 8), correspondente ao dia 5 de abril. Este novilúnio tem o seu plenilúnio correspondente no dia 18 de abril.
Em resumo, a Lua Cheia Pascal pode acontecer entre 21 de março e 18 de abril. Daqui podemos retirar o intervalo de datas que o Domingo da Páscoa pode ocupar. Supondo que temos plenilúnio a 21 de março, o domingo mais próximo poderia ser a 22 de março. Se 18 de abril albergar o plenilúnio e for um domingo, a Páscoa será no dia 25 de abril, o domingo seguinte, nunca depois. Ergo, sabemos que a data do Domingo de Páscoa será sempre entre 22 de março e 25 de abril.
- A implementação do ciclo na estrutura do Calendário Juliano no Ocidente latino medieval resultou, no seu desenho mais comum, na disposição que podemos consultar neste Almanaque Lunar Perpétuo.
Convém aqui voltar a referir que os procedimentos do cômputo conseguem evitar a utilização de frações, simplificar as complexidades e variações dos verdadeiros ciclos astronómicos:
- O Ano Tropical (determinado pelo movimento de revolução da Terra tendo como referência o Equinócio Vernal, isto é, o início das estações). O período compreendido é de 365,2422 dias solares médios.
- O Período Sinódico lunar ou mês sinódico (tempo decorrido entre duas luas novas consecutivas). Este período tem a duração de 29,53059 dias.
- Há uma diferença de cerca de 11 dias entre o ano solar (aprox. 365 dias) e o lunar (12 lunações de cerca de 29,5 dias cada = aprox. 354 dias). Ver definição de Epacta.
Numa definição simples, um calendário lunissolar procura iniciar cada mês numa lua nova e, simultaneamente, o ano numa determinada estação. (Fotheringham, J. K., The Date of the Crucifixion in: The Journal of Philology, 1903, vol.XXIX, N.57, p.101). Mas como vimos, nem o ano solar nem o lunar possuem um número inteiro de dias, Obviamente não faria sentido, em qualquer calendário, utilizar ‘frações de dia’ ou outras "minudências". Não há como compatibilizar ambas as vertentes sem que haja "ajustamentos" artificiais conciliatórios. As técnicas utilizadas incluiram recorrer a ciclos de relacionação, arredondar e intercalar ou suprimir dias, tendo em vista o cumprimento de regras adotadas a priori.
N.B.: no mais recente Calendário Gregoriano, o ajuste do ciclo lunar receberá o nome de proemptose ou Equação Lunar, e o ajuste do ciclo solar metemptose ou Equação Solar. O termo aequatio significava justamente “tornar igual” ou “nivelar”. Na prática, neste sistema, a Equação Solar é a eliminação ocasional de dias (bissextos) do calendário solar. Equação Lunar é a eliminação ocasional de um dia de um mês lunar (aumentando um dia à "idade" da Lua), refletindo-se ambas no calendário final (ver detalhes)
Enneakaidekaeteris - o Ciclo Metónico
Veja-se a seguinte listagem (James Evans, The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p.189). Apresenta, para cada ano, a data da sua primeira Lua Nova.
Verifica-se que estas datas deambulam (no calendário) ao longo dos anos
da tabela. Todavia, após 19 anos (cf. datas dos primeiros e últimos anos elencados), verifica-se
uma quase coincidência nessas mesmas datas (entre 1961 e 1980, entre 1962 e
1981 e entre 1963 e 1982). O mesmo se verificaria se a tabela
continuasse.

Acresce
que, num dado ano, para conhecer os novilúnios dos meses seguintes,
basta adicionar, alternadamente, 30 dias e 29 dias (meses plenos e
meses incompletos) à data da 1ª Lua Nova, e.g., para 1963 (começando em 25 de Janeiro) teríamos:
+ 30 dias = 24 de Fevereiro (2ª Lua Nova do ano)
+ 29 dias = 25 de Março (3ª Lua Nova do ano)
+ 30 dias = 24 de Abril (4ª Lua Nova do ano)
+ 29 dias = 23 de Maio (5ª Lua Nova do ano)
etc.
Percurso histórico deste ciclo
Lis Brack-Bernsen e Hermann Hunger (The Babylonian Zodiac: Speculations on its invention and significance, Centaurus 1999: Vol. 41, p.287), referem que o ano babilónico era composto por 12 ou 13 meses lunares. A partir de cerca de 500 A.C., um ciclo de 19 anos regulava a intercalação do eventual 13º mês, necessário para que o Equinócio Vernal caísse no ou próximo do 1º mês, Nisanu (também transliterado Nisannu). Sendo a "matriz" do ano Judaico, começava no novilúnio após o Equinócio vernal e compreendia doze meses lunares, cada qual começando no primeiro avistamento do crescente: Nisanu, Aiaru, Simanu, Duzu, Abu, Ululu, Tashritu, Ahrasamnu, Kislimu, Tebetu, Shabatu, Addaru; os dias começavam ao pôr do Sol e eram contados de 1 a 29 ou e 1 a 30. Ainda se discute quendo é que as intercalações (para o acerto com as Estações do Ano) deixaram de ser ad hoc e passaram a ter um esquema definido. Segundo Holford.Strevens, sabemos que a partir do séc. IV a.C. Addaru era repetido nos anos 3, 6, 8, 11, 14 e 19 do ciclo (que conhecemos como "Metónico" mas que já era utilizado na Mesopotâmia), e o mês Ululu no 17º ano.
Sem
surpresa, o cômputo recorreu desde muito cedo a interpretações desta
útil correlação. O ciclo
que ficou conhecido como "Metónico", ou Enneakaidekaeteris foi atribuído pela tradição literária aos gregos Méton e Euctemon e supostamente gizado circa 433 a.C. (Segundo Alexander Jones, a atribuição a Méton é feita por fontes tardias (incluíndo Diodorus, Bibliotheca Historica 12.36, Milet inv. 84 + inv. 1604, e o pseudo-Theophrastus, De Signis).
Atendendo a que as intercalações do calendário babilónico eram
reguladas, como vimos, por um ciclo de dezanove anos pelo menos desde o
séc. IV a.C. (talvez mesmo desde o séc. V), será tentador pensar numa
influência. Todavia, atendendo à
relativa facilidade na identificação deste ciclo e pelo facto de os
antigos chineses o terem também utilizado, não podemos descartar uma
descoberta independente na Grécia. (Greco-Roman Astrology and Astronomy, in Jones, A. and Taub, L. (eds.), The Cambridge History of Science, Vol I, 2018: 382). Este é mais um de tantos ciclos que foram laudatoriamente chamados "Grande Ano" (Censorinus 18,8, ed. Huitsch, p. 38, 9-12).
Para alguns autores cristãos, a ideia de que o prestigiado ciclo teve origem angélica (divina) era evidente (v. Epistola Cyrilli, edit. por Bruno Krusch, Leipzig 1880: 344–49). Pelo menos desde o séc. IV, afirma-se também a interpretação (sem respaldo histórico) de que emanou do Sínodo de Niceia (actual Íznik, na Turquia), e.g., Aurelius Ambrosius (Santo Ambrósio de Milão), Epistula extra collectionem 13, ed. M. Zelzer, CSEL 82 (Vienna 1982): 222–34, embora autenticidade da missiva seja disputada; Dionysius Exiguus, Ep. Ad Petronium, ed. Krusch, Studien II: 63–68, p.63.
O
calendário lunar acompanha as fases lunares, o solar o desenvolvimento
das estações do ano. Segundo este ciclo, 235 meses lunares correspondem
exatamente a 19 anos trópicos. Eis uma ponte fundamental entre dois
ciclos aparentemente irreconciliáveis e a ferramenta mais importante
para os computistas: 19 anos de 235 meses contém um número integral de dias. O ciclo recorre, na vertente solar, a anos tropicais, i.e.,
intervalos astronomicamente definidos. Aí se integram 235 meses lunares
médios, que no final conciliam a mesma fase lunar com a mesma estação
(momento em relação à estrutura de equinócios e solstícios), mas
depende do calendário "local" específicamente utilizado se se
sincroniza ou não também com a data.
Para o agilizar, utilizou-se a intercalação de meses adicionais em determinados anos do ciclo (totalizando 12 anos lunares de 12 meses cada e 7 anos embolísmicos de 13 meses cada), em função dos valores acumulados dos desfasamentos, i.e., epactas. É por intermédio dos meses intercalados que o calendário eclesiástico restabelece o início do ano lunar, quando se encontra atrasado. Daqui se deduzem as 235 lunações (12 x 12 + 7 x 13). Ver breve resumo do funcionamento. O mês lunar astronómico possui aproximadamente 29,5 dias. O cômputo criou a ficção da alternância entre meses de 30 e 29 dias (procurando replicar a mecânica dos meses solares). Para responder ao nº de lunações necessárias, procurou-se colocar os meses lunares intercalares de modo "discreto", utilizando, sempre que possível, meses solares nos quais as lunações terminassem nos primeiros dias. Acomoda-se deste modo o mês embolísmico. No mês solar sequente, este mês (lunar) estará concluído nos primeiros dias, dando lugar ao seguinte sem perturbações maiores.
O
ciclo surgirá sob numerosos "disfarces", por exemplo na tabela de 95
anos (múltiplo de 19) que Isidorus Hispalensis (Isidoro de Sevilha) e
outros utilizaram (McCluskey, 2013: 296). Outros ciclos estavam
disponíveis (e.g., o chamado octaeteris, de 8 anos,
outro de 11). Um ciclo de 84 (múltiplo do ciclo solar de 28) granjeou a
preferência romana, talvez numa tentativa de contrariar a superioridade
alexandrina), mas o metónico apresentava maior precisão. O
ciclo dominante foi provavelmente introduzido no cômputo por Anatolius
de Alexandria, bispo de Laodiceia, no século III. Na Epistola ad Petronium, interpretada como um "prefácio" à sua tabela, Dionysius Exiguus atribui o desenvolvimento do ciclo de 19 anos, após Niceia, a Athanasius, Theophilus e Cyrillus (Krusch, Bruno, Studien zur christlich-mittelalterlichen Chronologie: die Entstehung unserer heutigen Zeitrechnung, Berlin, Akademie der Wissenschaften, 1938: 63). Cedo
se compreendeu que o desfasamento anual de um 1/4 de dia significava
que 4 destes ciclos asseguravam uma repetição mais aproximada das
datas. Uma referência deve aqui ser feita a Cálipo (Calippus) de Cízico, que,
ainda no século IV A.C., deu sequência à abordagem metónica,
verificando que uma maior precisão seria conseguida omitindo 1 dia após
cada implementação de 4 séries, criando, deste modo, um ciclo de 76
(19x4) anos que tem o seu nome. Perfaz 27759 dias e articulava-se com o
Calendário Alexandrino. Integrado com um ciclo que acautela os 7 dias
da semana, constitui um ciclo (7 x 64 = 532 anos) adoptado, por exemplo, pela igreja monofisita Etíope (Neugebauer, O., HAMA: Op. cit, p.624).
Como R. R. Newton salientou, os ciclos são quase-coincidências. Acrescentado adiante: all cycles will fail when carried far enough (Ancient Astronomical Observations..., The Johns Hopkins Press, 1970, p.66). Com o tempo, o ciclo de dezanove anos revelou desfasamentos. Philipp Nothaft (The Astronomical Data in the Très Riches Heures and their Fourteenth-Century Source,
in: Journal for the History of Astronomy, 2015, Vol. 46(2) 113–129),
refere-se à utilização das sizígias astronómicas (em detrimento das
convencionais), conhecidas a partir de tabelas (e.g.,
Toledanas, Afonsinas) como prática relativamente comum, que
encontramos, por exemplo, em Petrus de Dacia, Walter Elveden, Johannes
de Gmunden (lat. Johannes de Gamundia) ou Nicholas de Lynn. O
problema residia no facto de o ciclo convencional de dezanove anos ter
sobrestimado a duração do mês sinódico em cerca de 23 segundos. Isto
equivale a um dia em aproximadamente três séculos. No início do século
XV, a discrepância entre as luas novas do calendário e as verdadeiras
(astronómicas) ascendia a cerca de 3 ou 4 dias. De facto, por esta e
outras razões, o tema de uma possível reforma do calendário preocupou o
Papa Clemente VI (1342–1352). A inclusão de um áureo número "renovado" ("Nombre d’or nouvel") numa das colunas do calendário nas célebres Très Riches Heures du Duc de Berry
(1416) não se tratava de um novo esquema cíclico (pois este teria a
mesma imprecisão na raíz) mas pretendia proporcionar informação mais
precisa ao longo do período contemplado. Esta informação seria
extremamente útil, por exemplo, na prática médica.
.
Decemnovennalis versus Lunaris
O ciclo chamado decemnovennalis é uma implementação alexandrina do metónico, sendo o nº de ordem determinado por uma opção utilitária, empiricamente descoberta, de associação dos novilúnios ao calendário solar (neste caso a data primaveril convencional do "domicílio" da epacta alexandrina, equivalente ao dia 22 de março Juliano), Nesta data, a epacta é nulla no ano I do ciclo. A Lua Nova associada ao dia 1 de janeiro (início do ano no Calendário Juliano) veio, de modo contingente, a pertencer ao ano III (considerando os novilúnios do referido calendário, no ano III deste ciclo é que o 1º novilúnio acontece no dia 1 de janeiro, ver tabela).
O sistema dos números áureos foi introduzido somente no séc. VI mas foi considerado como se houvesse sido adoptado no Concílio de Niceia, dois séculos antes. O ciclo foi preparado de modo a iniciar convencionalmente num ano em que um novilúnio caísse a 1 de Janeiro. Retrocalculando, a cronologia chegou ao ano que precede o início convencional da era Cristã (1 AD). Dionysius Exiguus, ao estabelecer a sua nova Era Cristã, fez a escolha opcional do ano equivalente a 1 a.C como o 1º da série.
Concitando a unanimidade dos autores do passado, este ciclo denunciaria a influência "dos hebreus" (Hebraeorum institutione), interpretação provavelmente respaldada na exegese vetero-testamentária e na autoridade que esta traduzia. Segundo Beda, interpretava a "observância prescrita na Lei dos Judeus" (Wallis, 1999: 139). Ainda presente nos tratados de cronologia dos séculos XVIII e XIX, é extrapolada da relação com o mês ("Pascal") de março (que existe sobremaneira pela razão acima exposta, a sedes epactarum, data de referência da epacta, expediente servindo o cômputo pascal).
Este ciclo precede em 3 anos uma "réplica", o chamado cyclus lunaris, o lunae circulus de Dionysius (Mosshammer, 2008: 85). Com origem indeterminada, chegado ao ocidente através da tabela pascal do pseudo-Cyrillus (Wallis, 1999: 346), era chamado "dos romanos" (e.g., por Beda, visto seguir a lunação de janeiro). Era, segundo o Manuel de Diplomatique de A. Giry (p.148), o "dos Gregos", sendo utilizado pelos Israelitas que o adoptaram no séc. IV. Foi amiudadamente confundido e designado pelos mesmos nomes na idade Média. Holford-Strevens refere que o ciclo lunar da tabela era o usado em Constantinopla, desfasado 3 anos atrás do alexandrino (Op. cit., 2005: 49). O seu ponto de partida era o ano 3 d.C. Foi utilizado na tabela pascal do 'Venerável', seguindo o exemplo da influente listagem de Dionysius, provável causa da sua visibilidade. É hoje interpretado como uma referência "cruzada" e alternativa. A vantagem seria, como veremos, conhecer facilmente a "idade" da Lua no dia 1 de janeiro.
Tabela Pascal. Listagem tem início no A.D. 988 (DCCCC LXXXVIII), apresentando a habitual coluna com sequência do Cyclus Lunaris (a partir do nº de ordem XVII, equivalente ao ano I do decemnovennalis), seguindo o exemplo da tabela de Dionysius. Esta série contempla a transição do 1º milénio; Ms. do século XII, compilando trabalhos de Beda, Hyginus e Abbo Floriacensis (folio 24r, Sp Coll MS Hunter 85 (T.4.2), Durham)
Os Beneditinos de Saint-Maur (L' Art De Verifier Les Dates Des Faits Historiques Des Chartes,…, Première Partie, Paris, 1710, xxxv), registam versos medievais que distinguem estes ciclos de modo conciso: Muta Cyclum lunarem in Kalendis Januarii, Cyclum decemnovennalem in Kalendis Martii. Pois o primeiro seria regulado pela lunação de janeiro, o segundo estaria vinculado ao chamado "mês pascal".
Num exercício de especulação erudita, Denis Pétau, latiniz. Petavius (1583-1652), o eminente filólogo e teólogo jesuíta (Doctr. Temp. vi. 5), estuda o seu lunaris latinorum que acredita ter sido conhecido e utilizado em Roma desde a instauração do Calendário Juliano, gizando até um "almanaque" lunar perpétuo à semelhança do convencional baseado no "Áureo Número" (nº de ordem no ciclo decemnovennalis), antecipando os números duas unidades (e.g., colocando, como seria correto nessa perspetiva, o nº ordinal 1 no dia 1 de janeiro, onde temos o nº 3 segundo o ciclo decemnovennalis, etc). A sua suposição histórica não veio a ser, obviamente, comprovada. O ciclo primitivo utilizado pela Igreja latina era de 84 anos (referência infra).
Como resumirão os tratadistas, o nº de ordem de um determinado ano no ciclo decemnovennalis é sempre mais 3 unidades do que no chamado lunaris. Ambos são, todavia, interpretações convencionais do ciclo metónico, cada um com a sua aera (era, ponto de partida) específica e vínculo a determinada lunação privilegiada no calendário.

Correspondência entre os dois ciclos convencionais, in Zallinger J. A., Instititiones Juris Ecclesiastici Maxime Privati Ordine Decretalium, Liber V (Caput VIII), Romae, Collegio Urbano, 1832 (ed. princeps: Augsburg, 1792-3)
A confusão surge da sobreposição de ambos (Wallis, 1999: 294, 346). O cômputo tem origem no sistema alexandrino (cujo calendário começa no mês Thoth, equivalente a setembro), ou mais precisamente no seu ciclo das epactas, que escolheu convencionalmente como ponto de partida os anos do ciclo que possuem epacta nula no 26º dia de Phamenoth (equivalente a 22 de março ou "a.d.XI.Kal.Apr.", vertido para a datação romana), por razões relacionadas com a determinação da Páscoa e estabelecendo a data referencial do calendário para a sequente determinação das epactas anuais. Para trabalhar com o Calendário Juliano seria necessário "traduzir" a epacta para o dia 1 de janeiro, de modo a conseguir determinar as epactas mensais relacionadas com esta. Entretanto, documenta-se paralelamente esta série (lunaris) que se relacionava comodamente com a lunação de janeiro.
Prevalecerá, todavia, a "distribuição" dos números do ciclo segundo a lógica do ciclo decemnovennalis, no que pode ser chamado "almanaque lunar juliano normalizado", disponível na tabela perpétua (ver coluna dos Áureos Números, 'A.N.').
Esta implementação criou uma listagem dos valores da epacta que deve respeitar a epacta nulla do ano III do ciclo (ver). A normalização que subjaz à série do Áureo (i.e., "importante") Número (que assinala a luna prima) passa a ser o método privilegiado de indicação dos novilúnios nos calendários, materializando-se através da inscrição deste nº de ordem no ciclo. Segundo Walter van Wijk (Le nombre d'or : étude de chronologie technique suivie du texte de la Massa compoti d'Alexandre de Villedieu (c.1170-1250), La Haye: Nijhoff, 1936), tem primícias em Alexandre de Villedieu e Abão de Fleury, por volta do final do primeiro milénio. A partir do século XII os métodos de Beda são ultrapassados e a luna ("idade" da Lua para determinado dia) passa a ser inscrita diretamente nos calendário, associando os Áureos Números aos dias tabelados em que acontecem os novilúnios nos diversos anos do ciclo de 19. Também se assiste à implementação da Letra Dominical para a determinação dos dias da semana (feriae), em detrimento da utilização dos concurrentes dies.
Tecnicamente, considerando que a relação entre as fases lunares e os dias do ano obedece a um carácter cíclico (repetição das fases lunares nos mesmos dias do calendário), tornou-se óbvio associar um número de 1 a 19 a cada ano particular. Anos sequentes apresentam valores seguidos na série cíclica. Este elemento dá a conhecer as datas dos novilúnios para qualquer ano, essenciais para a determinação da Lua Cheia Pascal e consequente data da celebração maior. O Áureo Número (aqui não relacionado com a proporção ou secção áurea) adotado para cada ano solar apresenta valores de 1 a 19. A sequência acima, proveniente de uma edição de 1842 do Missale Romanum, apresenta os números começando pelo "6", este servindo 1582, anno correctionis, data da publicação da bula que instituiu a Reforma do calendário. Nesta data, já o Aureus Numerus tinha um longo percurso como ferramenta do cômputo. Muitos autores medievais reiteram as suas antigas e prestigiosas origens de modo laudatório. É o número mais importante pois, traduzindo o que Durandus (William Durand) escrevia em 1286 no seu Rationale divinorum officiorum: "...tal como o ouro supera os restantes metais, assim este número excede todos os restantes meios de cálculo lunar". Este legendarium medieval prevalecerá na literatura, com uma persistência assinalável. Todavia, as referências bibliográficas elencadas utilizando a "áurea" designação parecem recuar somente ao século IX (Philipp Nothaft, Scandalous Error - Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford/New York, Oxford University Press, 2018: 59). |
Por fim, para o cálculo do número de ordem no ciclo de 19 anos na implementação que prevaleceu, soma-se 1 unidade ao ano em causa (pois, como vimos, o "ponto de partida" adotado foi o ano prévio ao início da Era Cristã, i.e., 1 A.C.) e divide-se o resultado por 19. O remanescente é o nº de ordem, não havendo (nihil) prevalece o valor 19. Os Áureos Números são os mesmos para os calendários Juliano e Gregoriano.
Epacta (epaktai hèmerai, dies adjecti, "dias acrescentados") é o excesso de dias do ano solar sobre o lunar, traduzindo a "idade" da Lua (em dias) ou a fase para determinada data. Designa a quantidade de dias da lunação para uma data que, ano após ano, serve de referência no âmbito de um ciclo computista particular. Em suma, permite a relacionação das datas lunares com o calendário solar, no enquadramento da implementação metónica de dezanove anos. (Tratamos aqui da Epacta tradicional e não do complexo Cyclus Epactarum, inovação do calendário corrigido no séc. XVI)
| ................. | JAN. |
FEV. |
MAR. |
ABR. |
MAI. |
JUN. |
JUL. |
AGO. |
SET. |
OUT. |
NOV. |
DEZ | Total (dias) |
| Ano solar comum | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 | 365 |
| Ano lunar comum |
30 | 29 | 30 | 29 | 30 | 29 | 30 | 29 | 30 | 29 | 30 | 29 | 354 |
| Ano solar bissexto | 31 | 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 | 366 |
| Ano lunar bissexto | 30 | 29 | 31 | 29 | 30 | 29 | 30 | 29 | 30 | 29 | 30 | 29 | 355 |
Ano solar e ano lunar - diferencial (segundo Barradas, Aurélio. (2012). Martyrologium Lamecense (Texto e Comentário). [Tese Dout., Faculdade de Letras da Universidade de Coimbra], p.748)
A maior parte dos computistas, tal como Beda, optaram por vincular a Epacta ao dia 22 de Março,
por ser o primeiro dia onde podia caír a data da Páscoa. O valor
aumenta 11 dias em cada ano do ciclo de dezanove (cada ano é
identificado pelo seu Áureo Número). Se a epacta for nula num
determinado ano a 22 de Março, no ano seguinte será 11 nesse dia. E
assim sucessivamente. Ultrapassando 30, procede-se à intercalação de um
mês lunar. Como 19 x 11 = 209, num ciclo de 19 anos há 7 anos
"embolísmicos" (com mês intercalado). Ou seja, no ciclo de 19 anos há 7
intercalações de 30 dias (i.e. 1 mês lunar convencional dom 30 dias),
devido ao acúmulo do diferencial ao longo dos anos. Os 7 anos com 13 (e
não apenas 12) lunações eram, quase sempre, os 2º, 5º, 8º, 11º, 13º 16º
e 19º. Mas houve alguma diversidade nesta prática. Para o ajustamento
ser preciso, os computistas precisaram adicionar 12 dias em vez de 11
num dos anos do ciclo, geralmente no último: o "saltus lunae".
Note-se que o mês lunar tem, astronomicamente, aproximadamente 29.5
dias; os meses convencionais do cômputo evitavam as fracções e
possuíam, artificialmente, 30 ou 29 dias. Lunações de 30 dias eram
chamadas "plenas", de 29 dias eram chamadas "cavas" (fazia-se o cômputo
dos dias da lua em meses lunares alternados, de 30 e de 29 dias). Como
estas
lunações existiam com um propósito computista e já não tinham relação
com as observadas na natureza, tornou-se cómodo designá-las pelo nome
do mês em que terminavam. Por vezes, como Giry referia (Op. cit.,
p.156), podíamos assistir a situações singulares: se, por exemplo, se
verificava um novilúnio a 2 de Fevereiro, como consequência a revolução
lunar efectuava-se quase na totalidade nesse mês. Todavia era chamada
"Lua de Março" pois a lunação terminava no início deste último mês.
O incremento anual do valor para a data de referência é de 11 dias. Ou seja, a epacta aumenta e os novilúnios acontecem 11 dias mais cedo no ano sequente. Como Mosshammer salientou: "Theoretically, the epact 30=0 represents the new moon at its conjunction with the sun. The epact of 1 represents the theoretical West visibility of the first crescent of the moon. It is from that point as day one that the fourteenth day of the moon is counted." (2008, p.76).
Sequência: nulla (sem desfasamento), 11, 22, 3, 14, 25, 6, etc., nunca ultrapassando 30, limite de dias do mês lunar. Todavia, há um ajustamento a fazer devido ao acúmulo de 209 (11x19) dias nos dezanove anos do ciclo completo para que a nova série lunissolar comece sincronizada e o seu 1º ano possua epacta nulla (ver funcionamento).
A chamada "epacta alexandrina", introduzida no cômputo pelo Patriarca Demetrius I, era utilizada, como vimos, para determinar a "idade" da Lua no 26º dia de Phamenoth (equivalente ao 22 de março juliano, a sua "localização" ou sedes epactarum, limite mínimo para data da celebração da Páscoa). Correspondendo ainda ao valor do último dia intercalar do ano anterior, pode assumir-se que se refere ao início do ano (alexandrino) em causa (Mosshammer, 2008, 75-80).
Em resumo, a Epacta "alexandrina" usada pelos computistas medievais é nulla no dia 22 de março, correspondendo esta referência ao ano I do cyclus decemnovennalis e ao ano XVII do cyclus lunaris (que encontramos nas tabelas de Dionysius e Beda). Sendo normalmente vinculada ao ano Juliano (com início em Janeiro), convém referir que os computistas podiam, ao modo Alexandrino, começar a epacta a 1 de Setembro, como se do início do ano se tratasse ("...september mutat epactas"). Nesse caso, em documentos da época, a informação cronológica da epacta mudava para o "novo" ano em Setembro e surge aumentada nas datas do último trimestre do ano juliano.
[Já o 1º dia de Janeiro era data pivotal na renovação de outros elementos do cômputo: Et nota quod numerus lunaris et littera dominicalis mutantur annuatim in «festo Circuncisiones» (dos Estatutos sinodais da diocese de Rodez, 1289; Marténe et Durand, Thes. nor. anecd., T. IV, col. 764, cit. por A. Giry, p.105)]
A correspondência dos anos do ciclo (decemnovennalis) com as epactas anuais referidas a janeiro (e não a 22 de março como em Beda, et al.) é diferente e assume os valores seguidamente disponibilizados (verificar recorrendo à tabela de correspondência , e.g., epacta nulla
associada ao 3º ano do ciclo; a correspondência pode ser
testemunhada para o alinhamento dos restantes números e epactas).
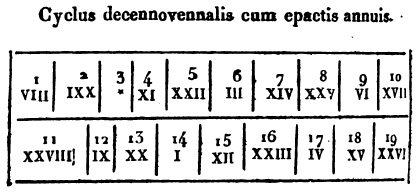
Epactas anuais no ciclo decemnovennalis, referidas ao Calendário Juliano, in Zallinger J. A., Instititiones Juris Ecclesiastici Maxime Privati Ordine Decretalium, Liber V, (Caput VIII), Romae, Collegio Urbano, 1832 (ed. princeps: Augsburg, 1792-3)
De novo a informação da epacta vinculada a janeiro para cada ano do ciclo (Butcher, Samuel, D.D., late Bishop of Meath. The Ecclesiastical Calendar: Its Theory and Construction, Hodge and Co., Dublin; Macmillan, London. 1877: 89), relacionando o Áureo Número ("G.N." - Golden Number) com a Epacta:
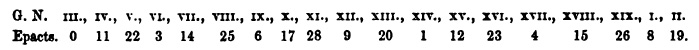
Saber o nº de dias que tem a Lua no início de cada mês e, particularmente, no dia 1 de janeiro (segundo Beda)
A "idade" da Lua para o início de cada mês, segundo Beda (cap. XX; Wallis, 1999: 64, 66), era conseguida adicionando um parâmetro (o regular mensal) à epacta anual ("idade" da Lua no referido dia 22 de março), que é nulla no 1º ano do ciclo decemnovennalis. (O regularis, entre outros expedientes, será exemplificado mais adiante)
Estes regulares mensais ou lunares (lunaris), exarados numa pagina regularum, serão (no ano I do ciclo. pela ordem dos meses, e assinalando a "idade" da Lua nas respetivas Calendas): 9, 10, 9, 10, 11, 12, 13, 14, 16, 16, 18 e 18. Utilizados no chamado sistema romano (em função do calendário que servem), ver infra.
O método de Beda para saber a epacta anual, seguindo Dionysius (Wallis, 1999: 135), é traduzível atualmente pela seguinte fórmula (sendo "A.D.", Anno Domini, o ano em causa): (A.D. mod 19) x 11 mod 30. (ver definição da operação módulo).
Assim, somando (inclusivamente) 9, o regular de janeiro, ao valor da epacta do ano em causa, determina-se a "idade" da Lua no dia 1 de janeiro. Todavia, como Beda reconhece, a mecânica dos meses lunares intercalados faz com que o método falhe nos anos VIII, XI e XIX.
- Ver MS 17 - Fol. 27r (Oxford, St. John's College): "rota" apresentando números que traduzem a “idade” da Lua para as kalendae de cada mês (meses inscritos sob o sinal cruciforme, de janeiro a dezembro, descendendo para o centro) para cada ano do ciclo decemnovennalis (à volta, na periferia, de I a XIX). Exigia ajustamento nos anos embolísmicos acima referidos.
Um método fiável, ensinado por Beda no seu De Temp. rat., LVII (baseado numa interpolação aos argumenta de Dionysius), utiliza comodamente o chamado cyclus lunaris (regulado pela lunação de janeiro) e não o decemnovennalis para saber a "idade" da Lua no dia 1 de janeiro. Multiplica-se o nº de ordem no ciclo por 11. Adiciona-se 1 (o regular de janeiro, pois neste ciclo lunaris o novilúnio acontece no 1º dia de janeiro do ano I; todavia, o regular será 2 para últimos 3 anos do ciclo, i.e., XVII, XVIII e XIX). Divide-se por 30 e o resto é o nº de dias da Lua no 1º dia do ano juliano.
E.g., o ano 534 da tabela de Dionysius refere que este é o 19º do ciclo lunaris, Verifica-se, na tabela "Conjunctio cycli..." que relaciona ambos os ciclos (acima nesta página), que corresponde ao 3º do decemnovennalis (para posterior confirmação). Assim, 19 x 11 = 209; 209 + 2 (regularis, ver regra ) = 211. Divide-se por 30 e o resto é 1. A Lua está no seu 1º dia (luna 1), equivalendo à epacta nulla (a epacta anual é a "idade" da Lua ab initio, no último dia do ano anterior, os "dias da Lua" no dia 1 de janeiro diminuídos de 1 unidade), Corrobora-se o resultado, por exemplo, na tabela "Cyclus decennovennalis cum epactis annuis", acima.

A "idade" da Lua no 1º dia de janeiro, segundo os anos do Cyclus Lunaris (para o dia 1 de janeiro do 19º ano do ciclo, a "idade" da Lua é I), in Zallinger J. A., Instititiones Juris Ecclesiastici Maxime Privati Ordine Decretalium, Liber V, (Caput VIII), Romae, Collegio Urbano, 1832 (ed. princeps: Augsburg, 1792-3)
A tabela acima permite extrapolar que sendo 1 o valor da epacta no 1º dia de janeiro no 19º ano deste ciclo (que corresponde ao 3º do decemnovennalis), a correspondente epacta anual será nulla (como referido anteriormente).
- Para saber o nº de ordem no ciclo (lunaris), subtraem-se 2 unidades ao ano em causa e multiplica-se por 19. O resto é o nº de ordem, não havendo será o 19º ano do ciclo.
Argumenta Paschalia
Tabelas de Dionysius, mosaico do século VI, Museo Arcivescovile/Opera di Religione della Diocesi di Ravenna
Em Dionysius, o Argumentum III. De epactis ("da epacta") é traduzível pela fórmula já conhecida: (A.D. mod 19) x 11 mod 30; O Argumentum VI. De cyclo lunari (nº de ordem na já referida implementação do ciclo, dito lunaris) é traduzível pela fórmula (A.D. - 2) mod 19.
Aqui o texto em latim do Argumentum III, onde o canonista utiliza como exemplo o ano 525: Si vis cognoscere quot sint epactae, id est adjectiones lunares, sume annos ab incarnatione Domini nostri Jesu Christi, quot fuerint DXXV. Hos partire per XIX, remanent XII. Per XI multiplica, fiunt CXXXII. Hos item partire per XXX, remanent XII. Duodecim sunt adjectiones lunares.
E agora o Argumentum VI, exemplificando com o mesmo ano de 525: Si vis scire quotus cyclus lunae est, qui decemnovennali circulo continetur, sume annos Domini, ut puta, DXXV, et subtrahe semper II, et remanent DXXIII. Hos partire per X et IX (i.e., XIX), remanent X. Decimus cyclus lunae est decemnovennalis circuli. Quoties autem nihil remanet, nonus decimus est.
Apesar de transcrever no Argumentum V a fórmula relacionada com o ciclo decemnovennalis, refletindo o que virá a ser conhecido como "Áureo Número" (traduzível por (A.D. + 1) mod 19), o computista replicou o formulado no supracitado Argumentum VI (neste caso referindo o nº de ordem do ciclo lunaris) na sua influente tabela pascal (que, segundo a sua missiva a Petronius, em tudo segue a que atribui a Cyrillus, exceto na inovadora utilização dos anos da Era Cristã).
Os computistas medievais digladiavam ambas as implementações cíclicas convencionais já referidas, designadas de modo pouco esclarecedor "lunaris" e "de dezanove anos" na obra de Beda (Wallis, 1999: 142) e daí em diante. Chamar-se-á "Áureo Número" ao nº de ordem no ciclo "de dezanove anos", decemnovennalis. Enquanto a fórmula relacionada com o cyclus lunaris indica que previamente se subtraia 2 unidades ao valor do ano (et subtrahe semper II), na implementação que prevalecerá adiciona-se, como exarado no Argumentum V, 1 unidade.
Segundo João P. Ribeiro (Dissertacoes Chronologicas E Criticas Sobre A Historia e Jurisprudência..., Tomo II, Lisboa, Academia R. das Sciencias de Lisboa, 1811), "A razão da diferença consiste em que o 1.° anno de J. C. tinha o Aureo numero , ou Cyclo Decemnoval 2 , e o Cyclo Lunar 18." (p.39).
Resumo
A Epacta "antiga" assume sempre apenas dezanove valores possíveis (revelando o seu carácter convencional e nocional), em função do nº de ordem de determinado ano no ciclo de dezanove (ver tabela seguinte, incluindo a vugar (alexandrina, adoptada por Dionysius ou Beda) e a "tradução" romana ou juliana deste parâmetro, vinculada ao 1º dia do mês de janeiro no Calendário Juliano). No Calendário Gregoriano a relação direta deixará de existir.
Decemnovennalis |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
Lunaris |
17 |
18 |
19 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Epacta |
0 |
11 |
22 |
3 |
14 |
25 |
6 |
17 |
28 |
9 |
20 |
1 |
12 |
23 |
4 |
15 |
26 |
7 |
18 |
Epacta ("romana") |
8 |
19 |
0 |
11 |
22 |
3 |
14 |
25 |
6 |
17 |
28 |
9 |
20 |
1 |
12 |
23 |
4 |
15 |
26 |
Epacta anual (original e na "tradução" romana), segundo o nº de ordem nos cyclus decemnovennalis e lunaris
A epacta "alexandrina" (que é a Epacta
propriamente dita, v. penúltima linha da tabela acima) assinalava a
"idade da lua" no dia 22 de março. Aquela a que podemos chamar “romana”
ou “juliana” é o mesmo fenómeno calculado para o 1º dia de janeiro: era
a “idade da Lua” (aetas lunae)
no arranque do ano Juliano. Equivalendo a 8 no 1º ano do
ciclo de dezanove, na prática a “idade da Lua” seria 9 (8 + 1) no dia 1
de Janeiro de qualquer ano cujo A.N. = 1. Neste caso, a Lua Nova
(i.e. lua com 29 ou 30 dias de "idade") seguinte seria a 23 de Janeiro (v. tabela juliana perpétua: Áureo
Número 1 responde ao dia 23 de janeiro).
Entretanto, surgiu na tratadística posterior à correção do calendário, o cálculo de uma suposta epacta "juliana", i.e.,
anterior à "correção", que determinava o valor 11 para o ano I do ciclo,
22 para o ano II, etc. Mencionado até antes da própria correção, (encontra-se, por exemplo, numa tabela do Reportorio dos Tempos de Andrés de Li, [Lixbõa : per Germão Galharde, 1552]). O Missale Romanum
inclui esta correspondência (que a sua autoridade decerto disseminou).
Contudo, a explicação parece-nos muito simples e somente pedagógica: a epacta é 11 no primeiro ano
tão somente porque (como se lê no Missale) "...cum hoc numero [i.e. 11] annus solaris communis lunarem annum communem excedat;". Ou seja, é apenas a constatação do diferencial de dias (ano solar - ano lunar), sem intenção computística. Trata-se da explicação da mecânica metónica
e do acúmulo do diferencial, não da agilização de uma solução funcional
em particular, com a sua relação cronológica concreta, como são os
ciclos decemnovennalis ou o lunaris, entre outros. Essa
"modalidade", na prática, seria espúria, não correspondendo ao uso nos
documentos tabeliónicos, dos notários ou das chancelarias do passado. João P. Ribeiro, nas suas Dissertacoes Chronologicas..., menciona-a mas decide pela "authoridade dos documentos", onde encontra exarada a que chama "epacta vulgar" ou "vulgar dos antigos":
"Assim considerão a correspondencia das Epactas com o Aureo Numero Clavio , e outros Computistas, tratando da Epacta Juliana, ou anterior á Correcção Gregoriana ; mas resiste-lhe a authoridade dos Documentos anteriores á mesma Correcção, que datão da Epacta 29 [com o saltus lunae do final do ciclo passa a 30] ou nulla , correspondendo ao Aureo Numero 1 ; da 11 , correspondendo a 2 ; e assim por diante, como se verá da Tabella." (Tomo II, p.45, nota (a)). Confirma, pouco depois: "...a Epacta, que vemos empregada nas datas dos antigos Documentos, e chamamos Epacta vulgar, exprimia o numero de dias, em que nesse anno cahem mais cedo os Novilunios, que no 1 º anno do Aureo Numero. A mesma (segundo o testemunho de Beda) exprimia tambem o numero de dias , que tinha a Lua a 22 de março , e servia a mostrar se a Lua , que então corria era a Paschal ( o que só podia ser tendo então a Lua menos de 16 dias ) :Os mesmos Computistas , ou mudavão a Epacta no 1.º de Janeiro com os Romanos, ou no 1.° de Setembro antecedente ao computo Romano com os Gregos e Egypcios. De huma , e outra Epacta ( chamemos-lhe Romana, ou Grega ) ha exemplos em datas de Documentos." (p.46).
Em suma, a modalidade encontrada na usual datação de documentos medievos (sendo a informação cronológica por vezes agenciada recorrendo à epacta e a outros argumentos do cômputo) documenta a utilização dos procedimentos que enformam os "princípios alexandrinos". É a conclusão que encontramos numa antiga obra pioneira da ciência histórica, da diplomática e da cronologia (De Saint-Allais, M., L'art de vérifier les dates des faits historiques, des chartes..., Tome premier, Paris, 1818, p.93): "Dans ces chartes de différents pays, les épactes sont toujours marquées, suivant le calcul de nos anciens computistes, qui comptaient, ainsi qu'on l'a dit, autant d'épactes, chaque année, que la lune avait de jours le 22 mars."
Outra obra de cronologia confirma que computistas e notários latinos começavam a contagem, "à maneira dos Egípcios", no início de setembro, e não "como os Romanos", em janeiro (Hampson, R. T., Medii ævi kalendarium: or dates, charters, and customs of the Middle Ages..., Vol II, H. K. Causton and Co., London, 1841: 116). Esta diferença na contagem é facilmente explicável: o ano Alexandrino começava no mês equivalente ao mês de setembro que precede o início do ano Juliano (epactas eram coincidentes ao longo dos primeiros 8 meses deste último). Daí a já referida expressão: "...september mutat epactas".
Houve, como vimos, uma tradução "romana", com menor visibilidade, que utilizou o valor da epacta associado (i.e. calculado para) ao início do ano Juliano, em janeiro (v. tabela supra). Mas nunca aquela acima referida (ano I = 11, ano II = 22, etc.). É evidente que num ciclo se poderia optar por qualquer data convencional de partida. Todavia, a prática computista anterior à correção confirma plenamente a conclusão de J. P. Ribeiro e dissipa o equívoco.
Entretanto,
em diversos tratados da centúria anterior à "correção" gregoriana,
encontramos uma estrutura de capítulos que inclui uma sequência
"padrão" dos elementos do cômputo que descarta a epacta. Um exemplo é o
Computus novus & ecclesiasticus: totius fere astronomie fundamentum pulcherrimum continens… de Petrus Liechtenstein, ed. 1519, que apresenta o seguinte alinhamento: De Aureo Numero, de indictionis, De Ciclo Solari, De littera Dominicali, De Intervallo e De concurrentibus, contemplando
seguidamente as cinco celebrações móveis consideradas essenciais, com
outros capítulos dedicados a temas astronómicos que encontramos
habitualmente nos tratados do tipo "sphaera" (descrição do
universo, os elementos, etc.). Alguns tópicos referentes ao cômputo
constituem alternativas eventualmente redundantes (e.g., concurrentes septimanae dies e litterae dominicales), inseridos somente por tradição ou pedagogia.
Vamos relacionar os elementos que conhecemos até aqui. Como vimos, o ano tropical solar possui cerca de 365 dias. O mês sinódico lunar cerca de 29,5 dias (resultando num ano de lunações com cerca de 354 dias). 19 anos tropicais equivalem a 235 meses sinódicos lunares (o ciclo metónico). Este ciclo pode conter 4 ou 5 anos bissextos no intervalo. O seu início é convencional.
A Epacta é determinada em função do nº de ordem de determinado ano no ciclo decemnovennalis. Se, por definição, traduz o excesso (arredondado para 11 dias) do ano solar sobre o ano lunar (365–354), o desenvolvimento deste ciclo determina o valor do desfasamento (i.e., Epacta) e a necessidade das intercalações (embolismos) convencionais.
Porque traduz a “idade” da Lua, o valor da epacta nunca ultrapassa 30 unidades (dias). Em 19 anos, o excesso de dias equivale a 209 (19x11). Estes dias suplementares vão integrar os 7 meses embolísmicos (209 / 7 = 29,85, i.e., ~30), contemplados pelos computistas e colocados quando exigidos pela ultrapassagem do limite da epacta.
Basicamente, intercala-se um novo mês lunar nos anos do ciclo em que se verifique um valor de dias adjecti acumulados que ultrapasse 30.
No início os anos solar e lunar estão sincronizados. A epacta inicial considera-se nulla (cf. Durandus, Rationale divinorum officiorum, Lib. VIII. Cap. 7: "Primus annus Cycli nullam habet Epactam"), acrescentando anualmente os 11 dias do excesso, na sequência: nulla, 11, 22, 3, 14, 25, etc.).
No final do ano solar, e sendo o ano lunar (constituído por 12
lunações) mais pequeno, o desfasamento ascenderá a 11 dias. Em 3 anos,
o ciclo lunar antecipará o solar em 33 dias, exigindo a 1ª intercalação
de 30 dias e reduzindo a divergência para 3 dias. Após 3 anos, i.e.,
no final do 6º ano do ciclo, voltaremos a ter um desfasamento e, mesmo
após a intercalação, a divergência será aqui ainda de 6 dias. Quando,
acumulando, a divergência ultrapassar 30 dias, intercala-se outro mês
lunar de outros tantos dias. Chegados ao final do ciclo de 19 anos,
verifica-se a necessidade de um último mês embolísmico e o novo ciclo
(ano I) começa sincronizado.
Mas
há uma complexidade no caminho, o excesso de 1 dia. Visualizando de
novo o ciclo completo, 19 x 11 = 209 dias; dividindo por 30, o resto será
29 e não zero. Aqui acontecia necessariamente, como vimos, o ajustamento medievo
tradicional do saltus: omitia-se 1 dia para ajustar de novo ambas as “rodas” dos ciclos convencionais e conseguir uma epacta nulla no final do ciclo (McCluskey, Steven C., Astronomies and Cultures in Early Medieval Europe, Cambridge University Press, 2000: 81-82).
Deste modo, porque os ciclos acumulam 1 dia adicional, este deve ser omitido e a Lua "salta", ajustando-se novamente à fase astronómica. A diminuição do tamanho do mês que incluia o saltus, no último ano dio ciclo, tornando-o "cavo" ou incompleto (29 dias), conseguia o mesmo resultado, passando a ser o método 'clássico' privilegiado.
N.B.: Em contraste com outros ciclos, este não é comensurável com a semana, com a determinação das feriae (dias da semana). Quando a data da luna xiv é encontrada, torna-se necessário recorrer a um expediente para conhecer a feria e determinar o próximo domingo: a Páscoa. Para esse efeito utilizaram-se primitivamente os concurrentes dies (com origem pagã, correspondendo aos chamados "dias dos deuses") e relacionando o ano e a semana.
- Mnemónicas para conhecer anos, meses e dias das Intercalações ("embolismos") no ciclo de dezanove, segundo Figueiredo (Chronographia: Reportorio dos tempos..., Lisboa, 1603, fol.12): "Cesar, formam. habet, longam, orbe, ruente, tenebit".
Procedimento permitia saber o Áureo Número (A.N.) pela letra inicial de
cada vocábulo, segundo a sua ordem no abecedário. Por exemplo, a
terceira intercalação aconteceria num ano com A.N. = 8, pois a letra
"H" (de "habet") é a oitava do abecedário. Para saber o mês e o dia usava a sequência: "Mobilis, ibo, Cifos, medo, habeto, coevus". A inicial do vocábulo indicava o mês; a inicial da segunda sílaba desse mesmo vocábulo indicava o dia.
Como Denis Muzerelle explica, este "ano lunar" é uma ficção pois na realidade o ano solar não pode acomodar um número inteiro de lunações. A diferença acumulada corresponde à Epacta. Sempre que esta assumia um valor igual ou superior a 30, tornava-se natural intercalar ou englobar (gr. embolein) um mês suplementar no ano lunar, com o objectivo de compensar o atraso sobre o ano solar, pelo menos em parte. Assim, o ano lunar passa de 354 a 384 dias. Ao fim de 19 anos (ciclo baseado no chamado "Metónico"), os valores (i.e. o ano lunar e o solar) voltavam a "encontrar-se", com a diferença de 1 dia. Bastava aqui "saltar" o dia excedentário ("saltus lunae") e tudo ficava acertado para o início de um novo ciclo idêntico ao precedente. A tabela seguinte explica o funcionamento do algoritmo.
| ANO SOLAR (no ciclo de 19) |
12 Lunações (6x29 + 6x30) - antecipação |
TOTAL ("bruto") |
Lunação suplementar (intercalada) se Total "bruto" for igual ou inferior a 335 (365 - 30) |
TOTAL ("líquido") |
Antecipação do Ano Solar sobre a lunação seguinte = Epacta |
| 1 |
|
|
|
|
|
| 2 |
|
343 | - |
343 | 365 - 343 = 22 |
| 3 |
|
332 | 332 + 30 |
362 | 365 - 362 = 3 |
| 4 |
|
351 | - |
351 | 365 - 351 = 14 |
| 5 |
|
340 | - |
340 | 365 - 340 = 25 |
| 6 |
|
329 | 329 + 30 | 359 | 365 - 359 = 6 |
| 7 |
|
348 | - |
348 | 365 - 348 = 17 |
| 8 |
|
337 | - |
337 | 365 - 337 = 28 |
| 9 |
|
326 | 326 + 30 | 356 | 365 - 356 = 9 |
| 10 |
|
345 | - |
345 | 365 - 345 = 20 |
| 11 |
|
334 | 334 + 30 | 364 | 365 - 364 = 1 |
| 12 | 354 - 1 | 353 | - |
353 | 365 - 353 = 12 |
| 13 | 354 - 12 | 342 | - |
342 | 365 -342 = 23 |
| 14 | 354 - 23 | 331 | 331 + 30 | 361 | 365 - 361 = 4 |
| 15 | 354 - 5 | 350 | - |
350 | 365 - 350 = 15 |
| 16 | 354 - 15 | 339 | - |
339 | 365 - 339 = 26 |
| 17 | 354 - 26 | 328 | 328 + 30 | 358 | 365 - 358 = 7 |
| 18 | 354 - 7 | 347 | - |
347 | 365 - 347 = 18 |
| 19 | 354 - 18 |
336 | 336 + 30 - 1 (saltus) |
365 | 365 - 365 = 0 |
Resumo da agilização alexandrina adaptada à determinação da data da Páscoa (baseado em Nothaft, P., Scandalous Error - Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford/New York, Oxford University Press, 2018: 45 et seq.):
- Tudo funciona comodamente evitando fracções. O ano tropical (das estações, referência é o equinócio vernal) totaliza arredondadamente 365 dias. Uma lunação demora c. 29,5 dias. O ano lunar, ponderado astronomicamente, é de 354 dias (29,5 x 12), O excesso do ano solar sobre o ano lunar é, portanto, de 11 dias.
- O parâmetro fundamental é, portanto, a chamada Epacta, com incremento de 11 (mod 30). Como dissemos, traduz a “idade” da Lua logo nunca pode ultrapassar 30 dias. Corresponde à idade da Lua (em dias) numa data de referência empiricamente escolhida no Calendário Juliano. Na interpretação latina medieval do sistema Alexandrino a referência era a data de 22 de março.
- Os meses lunares 'convencionais' são aqui de 30 e de 29 dias, alternadamente sequenciados.
- O ciclo completo de 19 anos tropicais perfaz 209 dias de desfazamento (19 x 11).
São pois necessários 7 meses lunares extraordinários, intercalares, de 30 dias (N.B.: como veremos no desfecho, 6 serão plenos e 1 incompleto, de apenas 29 dias).
- Sempre que um ano bissexto aconteça neste intervalo de 19 anos (pode acontecer 4 ou 5 vezes; média = 4 e 3/4), 1 dia deve ser somado ao acervo de dias lunares contidos no ciclo. Todavia, esta adição não interfere com o cálculo da Epacta, que aumenta sempre 11 unidades, quer o ano seja comum ou bissexto.
- Em média, fazendo o cômputo dos 7 meses intercalares e dos 4 dias adicionados nos anos bissextos, chegaremos ao total de 214 dias (7 x 30 + 4), resultando na soma total de 6940 (19 × 354 + 214) dias lunares no ciclo completo (354 é o número de dias do ano lunar, como sabemos). Verifica-se o excesso de 1 dia relativamente ao período de referência de 19 anos tropicais = 6939 dias. Para "acertar" esta conta é necessário subtrair 1 dia, Isto era feito preferencialmente no final do ciclo, tornando incompleto o último mês intercalar (reduzindo-a 29 dias): o saltus lunae (entendido como se a Lua saltasse um dia no seu caminho).
- .Assim, se o saltus for colocado no final do ano 19 este torna-se (por convenção, como sempre) embolísmico, com 383 em vez de 384 dias (estes 384 dias iniciais seriam os 354 originais do ano lunar + 30 do mês intercalado). A diferença epactal entre o final do ano e o 1º ano do novo ciclo cresce de 11 para 12. Deste modo, com 383 dias, a data do término (data limite) pascal cai de 17 para 5 de Abril e a Epacta aumenta de 18 para 30 (18 + 12 = 30, i.e. nulla), ver tabela seguinte, última linha. Tudo se sincronizava.
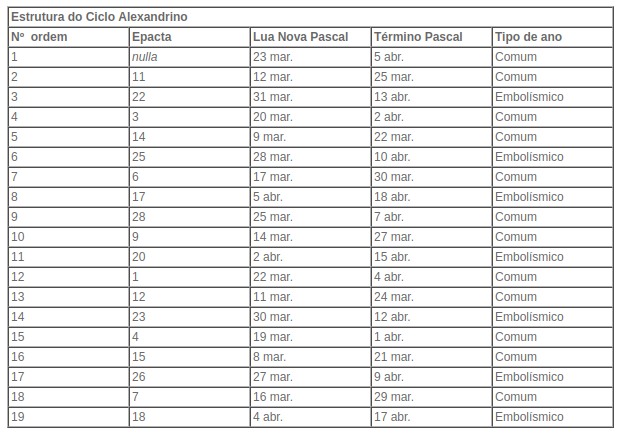
Estrutura do Ciclo Alexandrino (segundo Nothaft, 2018, Op. cit., table 2.1, p.47). O "Término Pascal" é, na prática, a data do plenilúnio Pascal (luna decimaquarta)

Voltando aos primórdios, para além da aparente contradição entre João e os restantes Evangelistas quanto à data/hora da Crucificação, surgiu a dificuldade causada pelo facto de o início do dia judaico acontecer ao pôr-do-Sol. Como saber quando é o início da noite do dia 14? Para uns (quintodecimans) seria no dia seguinte (opinião privilegiada pelas igrejas ocidentais). Algumas comunidades da Ásia Menor e da Síria celebravam a sua Páscoa "hereticamente" no próprio 14 de Nîsân (coincidindo com a celebração judaica e em qualquer dia da semana em que a data caísse), daí a designação (ou melhor, tradução) latina Quartodecimans. Condenados veementemente por, seguindo o dia judaico, celebrarem uma "Páscoa" da Crucificação e não da Ressurreição. Outras Igrejas, incluindo as do Ocidente, optaram por celebrar de modo independente da data judaica, no domingo após o equinócio vernal. Antioquia e Alexandria observavam o domingo mas a primeira ainda estava dependente da data da celebração judaica (por vezes erroneamente calculada, segundo críticas coevas), celebrando a Páscoa no domingo seguinte.
McCluskey (2000: 84) coloca até a questão da necessidade deste computus, atendendo a que o cômputo lunar judaico estaria disponível de longa data. Uma das razões que o autor adianta está relacionada com a necessidade de antecipação, conhecimento das datas prévias, preparação litúrgica inerente à celebração Pascal (e.g., os quadragesima dies). Seria mesmo assim exequível, apesar da dissonância entre diferentes procedimentos e observações referentes ao início dos meses lunares. A questão não é, conclui, astronómica mas sim institucional: o dictum tantas vezes repetido de que todos os Cristãos devem celebrar a Páscoa no mesmo dia. Sem esquecer que, na sequência de Niceia, se verificou uma persistente atitude crítica e até de confronto perante a imitação dos procedimentos do Calendário Judaico (Nothaft, Philipp, Medieval Latin Christian Texts on the Jewish Calendar - A Study with Five Editions and Translations, Leiden, Koninklijke Brill, 2014: 44).
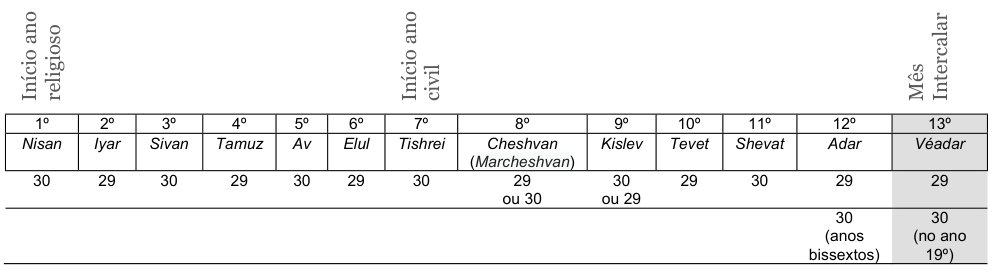
Meses do ciclo lunar Judaico convencional (adapt. de Aurélio Barradas,
p.737; v. Biblografia). O ciclo compõe-se de 19 anos (o que
também encontramos no nosso calendário eclesiástico). Doze anos
do ciclo são comuns (com doze meses); sete são embolísmicos (3.º,
6.º, 8.º, 11.º, 14.º, 17.º e 19.º) com treze meses (doze mais o mês
intercalar). Cinco meses são sempre plenos (30 dias); quatro sempre
cavos (29 dias); o décimo segundo mês é cavo nos anos comuns e pleno
nos anos bissextos; o oitavo e nono meses tanto são cavos como plenos;
o décimo terceiro mês é cavo no décimo nono ano do ciclo, e pleno nos
restantes seis anos embolísmicos. A intercalação do décimo terceiro mês
era calculada de maneira a que a Páscoa, celebrada no dia 14 de Nisan,
não chegasse antes do equinócio da Primavera. Aplicadas as regras, o
ano religioso judaico começa sempre (convertendo) entre 7 de Março e 5
de Abril.
Apesar da consciência da importância do calendário estar enraizada na cultura dos antigos Hebreus (e.g.,
Ex. 12,2), a diáspora fez com que muitas comunidades perdessem o acesso
à proclamação anualmente disponibilizada pelo Sinédrio (entretanto
dissolvido). A agilização do calendário era feita tradicionalmente com
a intercalação de um mês, um segundo Adar, de um modo guiado
pelas observações e aparências, não através de um procedimento
astronómico estabelecido como o ciclo metónico (Adam, 1990:6). E a
regulação das intercalações nos meses lunares é fundamental para a
correta determinação do chamado molad ("nascimento", plural moladot:
os novilúnios e os intervalos progressivos dos mesmos), do 1º mês e
datas relevantes. Esta normalização acontecerá somente no século IV,
atribuída ao rabino e patriarca Hilel II, que utilizará doravante como
matriz o desenho do ciclo metónico grego (Sasha Stern, Calendar and Community: A History of the Jewish Calendar, Second Century BCE to Tenth Century CE, Oxford/New York, Oxford University Press, 2001: 211 et seq.).
Tornando-se nocional e isento da observação do primeiro crescente
lunar, dispõe de um conjunto de regras relacionadas com o novilúnio do
mês Tishrei (ou Tishri), dia e parte do dia em que se verifica essa lua nova, bem como o dia específico em que o mês lunar começa.
Alexandria, recorrendo ao seu acervo de competências, calculava a sua data de modo autónomo e defendia que o domingo devia acontecer sempre após o equinócio. Como Holford-Strevens resume: "At Alexandria the old 8-year cycle had long been banished in favour of the Metonic cycle of 19 years with 7 embolisms; although the precise course of development is uncertain, by 323 at the latest the computus had reached its final form." (2005: 47). É, tradicionalmente, na sequência de Niceia que se assiste à consolidação dos cânones para a determinação da data da Páscoa no contexto da Cristandade, estabelecendo-se obviamente o domingo com veemência, adotando-se a perspetiva Alexandrina que se tornará exemplar (no século IV já se documenta a utilização conjunta da epacta e do ciclo metónico em Alexandria, sendo as tabelas articuladas com o calendário aí utilizado) e exortando-se à normalização dos procedimentos.
A Igreja de Alexandria permitia que a Páscoa acontecesse num intervalo entre os 15º e 21º dias da lunação, emulando os sete dias da semana hebraica dos Pães Ázimos (15 a 21 Nîsân), vide Ex. 12,18. Todavia, os bispos romanos insistiam que o Domingo de Páscoa nunca poderia ser celebrado antes do 16º dia da Lua, representando assim a data da Ressureição implícita no Evangelho de João, no qual, como sabemos, Jesus é crucificado no 14º dia de Nîsân (luna 14).
Esta controvérsia acrescida determinou, no Ocidente Latino, a urgência da criação de novas tabelas, ao cuidado de Victorius de Aquitânia (Aquitanus). Este compilou o seu Cursus Paschalis de 532 anos, recorrendo ao Ciclo Metónico (que utiliza na implementação "romana", utilizando a terminologia de Beda). Este "Grande Período Pascal" (também chamado a posteriori "Vitoriano" ou "Magno"), ao qual terá chegado acidentalmente pela via da cronologia bíblica (partindo do ano equivalente a 28 A.D. (ano no qual supunha ter acontecido a Paixão de Cristo), respaldando-se na crónica de Eusebius (na tradução de S. Jerónimo) e na sequência de São Próspero (Prosper Aquitanus), combina, na verdade, o ciclo lunar de 19 anos (recorrência de determinada fase lunar no mesmo mês e dia da semana) com o solar de 28 (7 x 4, quando os dias da semana voltam a assumir as mesmas datas nos meses do Calendário Juliano, que será base da determinação da chamada Letra Dominical). Na opinião de alguns especialistas (e.g., Jones, Charles W., The Victorian and Dionysiac Paschal Tables in the West, Speculum, 9, 1935: 409; Bedae Opera de Temporibus, The Mediaeval Academy of America, 1943: 63-5 ou Pedersen, Olaf., The Ecclesiastical Calendar and the Life of the Church, in: Coyne, G. V., Hoskin, M. A. and Pedersen, O. (eds.), "Gregorian Reform of the Calendar Proceedings of the Vatican Conference to Commemorate Its 400th Anniversary, 1582-1982", Pontificia Academia Scientiarvm, 1983: 48), Victorius aparentemente não se apercebeu da relevância do ciclo, talvez porque chegou aí partindo da mencionada e peculiar investigação cronológica. Segundo Faith Wallis, veria o seu ciclo como 4 x 133 anos, não 19 x 28, como Beda correctamente entendeu (The Reckoning of Time, Liverpool University Press, 1999, li). Como Beda explicou, 532 anos é o mais pequeno verdadeiro Ciclo Pascal no Calendário (Juliano). "The cyclical recurrence of all possible dates of Easter Sunday is determined by the least common multiple between this 28-year solar cycle and whatever lunar cycle is being used. In the case of the 19-year cycle, the answer is 19 x 28 = 532 years." (Nothaft, 2018: 47). Todavia, Alden Mosshammer (2008: 241), considerou estranho que esta multiplicação simples tenha escapado ao matemático Victorius. Em todo o caso, o período de 532 anos seria já reconhecido em Alexandria desde o início do século V (Nothaft, 2018: 47), mas as tabelas utilizavam, por comodidade, ciclos de apenas 95 anos (cinco séries de 19). A Tabela Pascal de Beda reconhece e consolida definitivamente a recorrência.
Victorius, ao procurar um compromisso, recorreu a procedimentos técnicos ecléticos (romanos e alexandrinos) e "irregulares", e.g. a colocação do "saltus" após o 6º ano e não no final do ciclo lunar de 19 anos, alterando a "idade" da Lua no restante percurso (referido por Beda, ver Wallis, 1999: Iii; Corning, 2006: 193, vide bibliografia), bem como uma imprecisa correlação com o mês lunar de Nîsân e os terminus da data da Páscoa, que antecipa de modo espúrio até ao próprio dia do equinócio a possibilidade da celebração (Wallis, 1999: 340). Parece aí ter seguido preferências romanas. As suas tabelas utilizavam os anos consulares e os annis passionis, que Dionysius e Beda substituirão pela Indicção e pelo anno domini, respetivamente. Resumindo o essencial, Victorius usou a implementação Alexandrina do ciclo de 19 anos mas com os limites xvi-xxii (e não xv-xxi como em Alexandria). As datas de Páscoa que se situassem entre 21 e 24 de março podiam conflituar com a celebração da Fundação de Roma (dia 21). Por isso, Victorius decide ocasionalmente exarar datas duplas à escolha dos responsáveis da Igreja Romana! Ademais, em certos anos, para celebrar a Páscoa antes de 21 de abril era obrigado a usar uma "Lua Cheia Pascal" espúria, que precedia o Equinócio! (MacCarron, M., Bede and Time..., Op. cit.: 5), Apesar de todos os erros e confusões, a tabela de Victorius aparentava ser completa, estruturava-se em relação ao dia 1 de janeiro e prometia uma determinação “perpétua” (os erros surgiam nos "pormenores"). O chamado laterculus Victorii mereceu particular atenção na Gália mas uma aceitação titubeante em Roma, abrindo caminho para a alternativa, através de Dionysius Exíguus.
Antes destas peripécias circulou em Roma, no início do século IV, uma tabela baseada num impreciso ciclo de 84 anos, a chamada Supputatio ("cálculo" ou "cômputo") Romana (que relacionava 1039 meses com 84 anos julianos e cujo período possuia a característica de ser múltiplo do ciclo solar de 28, cada ciclo começando no mesmo dia da semana que o seu antecedente), cuja origem é indeterminada e que, por diversas razões, se revelou insuficiente para a tarefa da determinação da Páscoa (Wallis, 1999: xlv). Era "...a shoddy piece of work that in some years gave two legitimate Easters, in others none." (Holford-Strevens, 2005: 47).
Entretanto,
numa particularidade insular, computistas das ilhas britânicas
recorriam a um ciclo pascal "arcaico" também de 84 anos, cujos detalhes
conhecemos através de autores como Beda, Columbanus e fontes
pseudoepigráficas. Foi trazido à luz por Daniel McCarthy e Dáibhí Ó
Cróinín (The "Lost" Irish 84-Year Easter Table Recovered, Peritia,
6-7 (1987-8), 225-42, posteriormente reimpresso e com argumentos
desenvolvidos em obras ulteriores). Este latercus de 84 anos, criado em terras Francas mas acima de tudo conhecido na versão insular (Mc Carthy, D. P., The origin of the latercus paschal cycle of the Insular Celtic churches,
Cambrian Medieval Celtic Studies 28, 1994: 25–49) baseava-se no
Equinócio de 25 de março e no ciclo solar de 28 anos, recorria (nesta
versão Céltica) a um "saltus" em períodos de 14 anos (o ciclo
romano anterior usava um "saltus" de 12 em 12 anos) e a um calendário
lunar pouco comum, com o número de dias de cada mês na sequência: 30,
29, 29, 29, 30, 29, 30, 30, 29, 30, 29, 30, 30.A hipótese entretanto
aventada da
relação com o Liber Anatolii de ratione Paschali (atribuído pela tradição ao bispo de Laodiceia mas amiudadamente considerado apócrifo e com origem insular), sendo o ciclo gizado por Sulpicius Severus (c.360-425) a partir de uma interpretação desse texto (aqui considerado genuíno), constituiu uma argumentação com visibilidade (McCarthy, Daniel P., e Aidan Breen, The ante-Nicene Christian Pasch: De ratione paschali. The Paschal tract of Anatolius, bishop of Laodicea, Dublin: Four Courts Press, 2003). É descartada nos detalhes por Mosshammer (2008: 138-140). Outros especialistas (Faith Wallis, Holford-Strevens e Immo Warntjes, referidos por Mosshammer, Op cit., 224) aprovam a reconstrução do ciclo mas questionam a autoria ou a relacionação. Wallis considera a autoria improvável, Holford-Strevens interpreta-o alternativamente como uma adaptação modificada de um ciclo com detalhes em comum criado pelo "obscuro" e difícil de datar Augustalis,
Warntjes nega qualquer relação com Augustalis e aceita a atribuição da
autoria a Severus. Seja como for, o ciclo de 84 anos será suprimido nas
ilhas britânicas pelo sínodo de Whitby (A.D.664), mas na prática persistiu em algumas comunidades.
A origem e prioridade deste ciclo divide, como vemos, os especialistas. Mas já em 1941 o jesuíta Peter Archer opinava com alguma lógica: "It was this defective paschal cycle that was received from Rome by the Celts at their conversion to Christianity, and was retained by the Celtic monks and missioners long after Rome had changed to a new cycle, thus giving rise to an Easter controversy in the West,..." (The Christian Calendar and the Gregorian Reform, Fordham University Press, 1941, p.17).
As tabelas definitivas
O padrão de oito colunas das tabelas Pascais prevalecentes desde a Alta Idade Média (ver exemplo1 e exemplo2), cuja afirmação se confunde com a história do cômputo, foi estabelecido tradicionalmente por Cyrillus de Alexandria, sendo replicado (Dionysius, Beda et al.) porque permite compreender a determinação das datas e, através da escolha específica deste conjunto de parâmetros (alguns dos quais, em rigor, redundantes), validar ou reafirmar os procedimentos adotados, na sequência das polémicas e controvérsias pretéritas.
O Ciclo Magno integra 532 anos, bastando substituir posteriormente os anos da sequência pois todos os parâmetros se repetem, configurando assim uma série perpétua. Victorius apercebeu-se da repetição mas não a compreendeu, Dionysius não a refere (provavelmente porque a relaciona com o computista mencionado). Beda terá estabelecido a estrutura fundamental deste ciclo (De Temp. rat., LXV), construíndo a sua Tabela Pascal de 532 anos (reproduzida em Wallis, 1999: Appendix 2).
No paper de Ulrich Voigt que anexamos (Likanas Verlag, Hamburg, 2014; PDF, 644KB), manifesta-se uma voz dissonante. O autor argumenta que a lógica prevalecente na instituição do fundamental ciclo de 532 anos terá sido "aditiva" e não "multiplicativa" (o ubíquo "19x28"). Desafiando a unanimidade académica (Wallis, Declercq, Strevens, etc.), despromove Beda do pleno entendimento da estrutura inerente, plasmada no mencionado capítulo do De Tempore Ratione. Acredita que, segundo o modus faciendi da época, outra seria a abordagem privilegiada. Acrescenta que o sistema prevalecente enferma de diversos problemas, nomeadamente devido ao posicionamento dos anos bissextos ao longo do ciclo e à necessidade de determinação da feria, dia da semana. Ademais, pela lógica matemática, um produto de anos resultaria em anos "ao quadrado"! Voigt apresenta tentativamente um conjunto de soluções esquemáticas recorrendo a parcelas. Afirma (com propriedade) o desacordo, já anotado por Petavius na sua Opus de 1627, entre Dionysius e Beda. Enquanto o primeiro utiliza uma tabela de 95 anos e omite o ciclo de 532, Beda compõe a célebre Tabela Pascal de 532 anos e nunca menciona o pretérito ciclo de 95. A tese conclui que os ciclos solaris, decemnovennalis e paschalis só podem ser interpretados na perspectiva argumentada, com parcelas, apresentando ad hoc decomposições plausíveis.
Influência das Tabelas Alexandrinas, Dionysius Exiguus e o Cômputo Medieval
|
Alexandria (pormenor), segundo Hartmann Schedel, Weltchronik [Liber chronicarum] Nürnberg: Anton Koberger, 1493
|
O cômputo teve origem em Alexandria. O intérprete "ocidental" que se revelará mais influente será Dionysius Exiguus ("Pequeno" ou "Humilde"). Provavelmente oriundo da Scythia Minor mas radicado em Roma, foi investido da ponderosa responsabilidade em 525 (na época designado ano 284 da Era Diocleciana ou dos Mártires). Desprezou, sem as mencionar especificamente, a relevância das tabelas em uso preparadas por Victorius (considerando que não estariam de acordo com os critérios alexandrinos e nicenos). Deste modo, não inovou mas recorreu e expandiu um conjunto de tabelas atribuídas (na tradição) a Cyrillus de Alexandria. Uma influência paralela de Exiguus reside na afirmação persistente de que a sua tabela traduzia fielmente a opinião do Concílio (Niceia), adotando de modo definitivo o ciclo de 19 anos (relacionação dos 235 meses lunares com os 19 anos, julianos) e fixando o equinócio em 21 de março. Estas "deliberações", já popularizadas por Ambrosius (bispo de Milão) no século IV, fizeram com que os princípios alexandrinos se revestissem de um prestígio inabalável junto dos computistas medievais. - Ver tabela gizada por Dionysius Complementarmente, por sua iniciativa, dá-se a substituição da Era de Diocleciano pela sua nova Era da Encarnação de Cristo. Através da posterior influência de Beda, tanto os critérios "nicenos" e alexandrinos como a nova aera assumirão definitivamente a centralidade que lhes reconhecemos.
|
Deve aqui referir-se que os calendários Alexandrino (instaurado/reformado pelo Imperador Augustus) e Juliano podem ser considerados "equivalentes", existindo uma reciprocidade que os torna mutualmente convertíveis. Um começa em setembro, o outro em janeiro: secundum AEgyptios, à calendis septembris; secundum Romanos, à calendis januarii (Beda). Ambos utilizam um ano bissexto ordinário com a mesma periodicidade (somente materializado em meses diferentes).
As tabelas alexandrinas começavam com o novilúnio (neomenia, que significava indiferentemente o novilúnio ou o primeiro dia do mês, v. Couderc, P., Le Calendrier, PUF, 2000 [1946], p.14) que aconteceu no dia anterior ao início da sua cronologia, equivalente a 29 de agosto de 284 (início da Era de Diocleciano). A Epacta
foi utilizada sem alterações pelo nosso computista, bem como um
parâmetro sequencial de números (de 1 a 7), relacionado com os dias da
semana e calculado anualmente (historicamente os "dias dos deuses
planetários" gregos ou "epacta solar"). Note-se que os diversos idiomas
europeus perpetuaram a relação dos dias da semana com os deuses e
planetas associados (por exemplo, segunda-feira, o "dia da Lua": Lunedi, Lunes, Lundi, Monday, Montag, Maandag, etc.). A exceção é o Português, onde utilizamos a ordem das "feiras". Segundo Emile Biémont (Rythmes du Temps: Astronomie et Calendriers, De Boeck, 1999), terá sido Martinho Dumiensis (i.e.
de Dume, 572-574), bispo de Braga, quem teria introduzido esta
"reforma", por achar intolerável que os dias da semana fossem
consagrados aos deuses pagãos. De facto, demonstra claramente a sua vontade"despaganizadora", por exemplo na epístola De Correctione Rusticorum, dirigida a Polemius, bispo de Astorga.
.
A sequência utilizada serve, como se sabe, para calcular o dia da semana (nº de ordem da feria) para qualquer data, Concurrentium hebdommadarum ratio, aritmeticamente muito simples devido à regular dimensão dos meses. A hebdómada parece ter sido instituída na época de Augustus, tendo no sábado o primeiro dia (o poeta Albius Tibullus refere o "dia sagrado de Saturno"). Para os cristãos será obviamente o Domingo.
A fórmula para calcular o concurrens dies (também chamado "epacta solar" ou Maior) pode assim ser traduzida: (A.D. + A.D./4 + 4) mod 7.
A
informação de Dionysius constituia uma série de 95 anos, a recalcular
após o seu limite, disponibilizada somente como listagem ordenada de
datas e parâmetros, ignorando o dia 1 de janeiro segundo o modus faciendi alexandrino. Gizada deste modo muito prático, os detalhes da estrutura e construção foram inferidos pelos computistas e assimilados na teoria: a epacta vinculada empiricamente ao dia 22 de março (26º dia do mês alexandrino Phamenoth, limite mínimo para data da celebração da Páscoa) e o locus concurrentium fixado no dia 24 de março, segundo Beda pela proximidade aos términos pascais (discussão da escolha desta data em Mosshammer, Op. cit., 81 et seq.).
Talvez apenas porque cai no mesmo dia da semana do que 24 de Fevereiro,
onde se inseria o dia extra nos anos bissextos (Georges Declercq, Anno Domini, The Origins of the Christian Era, Brepols, 2000, p.104)
.
Beda parece não ter sido familiar com a Letra Dominical, sistema mais tardio, similar ao dos concurrentes por ele descrito (De Temp. rat., LIII), denotando os dias da semana, feriae, nos quais o referido locus cai em anos sucessivos do ciclo solar (1 associado ao domingo, 2 à feria secunda e assim sucessivamente até ao 7, equivalendo ao sábado). Seria o nº de dias "supérfluos" que sobravam das 52 semanas (hebdomades) completas do ano antecedente e equivaleria ao dia da semana (feria) da referida data de 24 de março, contribuindo para conhecer o dia da semana para qualquer outra data. Todavia, verificou-se desde cedo a utilização de literae calendarum, suplementando o parâmetro mencionado.
Agilização
Na primeira tabela, que distribui o parâmetro pelos anos de ordem do ciclo solar (que é na verdade, "dominical"), os anos a negrito assinalam os bissextos. Esta tabela refere o cycli concurrentium. Este parâmetro, na sua ordem perpétua, pode ser associado diretamente à Letra Dominical (no 1º ano do ciclo solar o concurrente é 1 e a letra dominical seria "F", no 2º ano o concurrente é 2 e a letra seria "E", e assim sucessivamente), sendo um expediente de cálculo amiudadamente articulado com outros que veremos de seguida. A segunda tabela associa os concurrentes às letras dominicais (L.D.) e ao dia da semana.
| Ano do ciclo solar | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| concurrens | 1 | 2 | 3 | 4 | 6 | 7 | 1 | 2 | 4 | 5 | 6 | 7 | 2 | 3 | 4 | 5 | 7 | 1 | 2 | 3 | 5 | 6 | 7 | 1 | 3 | 4 | 5 | 6 |
(fonte: Butcher, Samuel, The Ecclesiastical Calendar: Its Theory and Construction, 1877: 83 et seq.)
| Conc. | L.D. | Dia semana |
| 1 | F | dom. |
| 2 | E | seg. |
| 3 | D | ter. |
| 4 | C | qua. |
| 5 | B | qui. |
| 6 | A | sex. |
| 7 | G | sab. |
As fontes primevas mais relevantes para o enquadramento dos procedimentos utilizados são os argumenta de Dionysius (nem todos genuinos, pois foram objeto de interpolações) e os De temporibus e De temporum ratione do Venerável Beda, referência prevalecente, a partir do século IX, pela vocação pedagógica da sua obra, influente até na terminologia adotada.
Os argumenta de Dionysius são pouco específicos quanto a alguns aspetos da metodologia utilizada na construção da sua tabela, por exemplo na distribuição dos meses embolísmicos ou no chamado saltus lunae, v. infra. Nem a data fulcral associada à Epacta foi por si explicitamente definida, mas, como referimos, empiricamente determinada pelos intérpretes da sua tabela (Mosshammer, 2008: 80).
Outros computistas estenderam e desenvolveram suplementos e algoritmos considerados úteis, amiudadamente dispensando a utilização de tabelas (elencamos seguidamente, baseados na sucinta exposição de Nothaft, 2018: 53 et seq., completando com outras fontes documentadas).
Um exemplo de procedimento complementar que recua ao século VII é a utilização de doze regulares solarium (ou mensium, mensais; hoje chamaríamos "reguladores", ver tabela infra) que podiam ser adicionados aos valores anuais dos referidos concurrentes, para descobrir o dia da semana do 1º dia de cada um dos meses julianos. Somava-se o regular do mês com o concurrente do ano em causa; se o total ultrapassasse 7 subtraía-se esse valor, sabendo então pelo nº do concurrente a feria, dia da semana (v. tabela supra). A dinâmica deste parâmetro pode ser comprovada deste modo: sendo, por exemplo, 5 o regular de março, somando os 31 dias deste mês chega-se ao valor 36. Dividido por 7, verifica-se o resto, que é 1. Este será o regular do mês seguinte.
Outra ferramenta eram os regularis ferialis (ou "Pascais"), sequência de 19 números que, combinados (somados) com os concurrentes, determinavam o nº ferial equivalente à data da Lua Cheia Pascal (luna decimaquarta, o término Pascal).
Os computistas gizaram, nos séculos imediatos, uma sequência de 19 chaves (claves terminorum) que, combinadas com datas referenciais (sedes clavium), tornavam possível determinar os términos no calendário para os cinco domingos medievos essencias: Septuagésima, Quadragésima (também chamada Initium), Páscoa, Rogações e Pentecostes.
O regularis ferialis e as claves assumem sequências de 19 números, denunciando a relação metónica. Deste modo, podem ser associados com o sempre fundamental nº de ordem no ciclo decemnovennalis.
| Nº de ordem ciclo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Regular Pascal | 5 | 1 | 6 | 2 | 5 | 3 | 6 | 4 | 7 | 3 | 1 | 4 | 7 | 5 | 1 | 4 | 2 | 5 | 3 |
| Claves | 26 | 15 | 34 | 23 | 12 | 31 | 20 | 39 | 28 | 17 | 36 | 25 | 14 | 33 | 22 | 11 | 30 | 19 | 38 |
(fonte: Butcher, Samuel, The Ecclesiastical Calendar: Its Theory and Construction, 1877: 87 et seq.)
Cada ano do ciclo possui a sua chave. A primeira é 26. As restantes calculam-se adicionando 19, tendo em conta que ultrapassando 40 se subtrai 30. O que resta será a próxima chave.
As 19 claves (cf. fólio do século XII, infra), eram cifras afetadas a cada ano do ciclo de dezanove que permitiam, somadas às datas dos términos de celebrações fundamentais, determinar as suas datas. A celebração acontecia no dia determinado ou, caso não fosse um domingo, no domingo seguinte. Ou seja, somadas (enquanto dias, inclusivamente) aos termini (datas referenciais tabeladas, associadas às celebrações), permitiam determinar a data destas no calendário. Se se tratasse da Páscoa, a chave somada (inclusivamente) a 11 de março daria a data da Lua Cheia Pascal. O dia da semana verificava-se com recurso aos concurrentes ou à letra dominical (ver exemplo). Em anos bissextos, 1 dia deveria ser adicionado às datas tabeladas abaixo para a Septuagesima e Quadragesima e se a última cair no dia ou após 24 de fevereiro, 1 dia deveria ser subtraído.
| Festa Móvel | Término |
| Septuagesima | 7 jan. (VII id. ian.) |
| Quadragesima (1º dom Quaresma) |
28 jan. (V kl. feb.) |
| Páscoa | 11 mar. (V id. mar.) |
| Dom. Rogações | 15 abr. (XVII kl. mai.) |
| Pentecostes | 29 abr. (III kl. mai.) |
Sedes clavium (fontes: De Saint-Allais, M., L'art de vérifier les dates des faits historiques, des chartes..., Tome premier. Valade, Impr. du Roi, Paris, 1818: 74; Hampson, R. T., Medii ævi kalendarium: or dates, charters, and customs of the Middle Ages..., Vol II, H. K. Causton and Co., London, 1841: 49)
Numa
curiosa correspondência terminológica, computistas e músicos
encontraram modos e termos paralelos para reconciliar e ilustrar partes
dos seus procedimentos explicáveis através de proporções (Kreitner K.
(Ed.), Renaissance Music, Routledge, 2016: 335). O mesmo pode
ser testemunhado na integração unificadora do universo do discurso da
generalidade das disciplinas medievais e renascentistas, consequência
da mundividência em presença. Síntese magnificamente ilustrada, através do que considera "O Modelo" medievo, por Clive S. Lewis (The Discarded Image, Cambridge, Cambridge University Press, 1964).
Quanto à “idade” da Lua (aetas lunae), o expediente já abordado, primeiramente descrito por Beda, é o conjunto dos 12 regulares lunaris.
Adicionados à epacta anual, permitiam determinar a "idade" (em dias) no
início de cada mês juliano. Existem dois conjuntos (“romano” e
"egípcio", i.e., alexandrino), referidos a 1 de janeiro (ou março, será equivalente) e setembro, respetivamente, como resposta à
diferença no mês inicial destes calendários. O princípio que subjaz é o
de que estes regulares mensais se referem ao 1º ano do ciclo,
bastando depois adicionar o valor da epacta do ano em causa. Para
calcular a "idade" da Lua, somava-se a epacta do ano, o regular mensal
e a data (sempre em dias), subtraíndo 30 sempre que o valor excedesse
esse número. A tabela seguinte inclui também o regular solar (vocacionado, como sabemos, para a determinação do dia da semana).
| jan. | fev. | mar. | abr. | mai. | jun. | jul. | ago. | set. | out. | nov. | dez. | |
| Regular lunar (romano) | 9 | 10 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | 16 | 18 | 18 |
| Regular lunar (egípcio) | 9 | 10 | 9 | 10 | 11 | 12 | 13 | 14 | 5 | 5 | 7 | 7 |
| Regular solar | 2 | 5 | 5 | 1 | 3 | 6 | 1 | 4 | 7 | 2 | 5 | 7 |
(fontes: De Saint-Allais, M., L'art de vérifier les dates des faits historiques, des chartes..., Tome premier. Valade, Impr. du Roi, Paris, 1818: 70 et seq.; Nothaft, 2018: 54 apresenta sequência diferente para os Regulares solares, a saber: 3, 6, 5, 1, 3, 6, 1, 4, 7, 2, 5 e 7, já utilizada por Petavius (cf. edição de 1736 do De Doctrina Temporum)
As sequências não incluem o zero, a contagem das datas deve ser sempre inclusiva, modo tradicional.
Exemplo: pretendemos saber a data do Domingo de Páscoa do ano (juliano) 2018. Por tabela ou processo aritmético determinamos o nº de ordem no ciclo de 19 anos, que é 5 (Áureo Número). Deste modo, pela tabela das claves, encontramos a chave "12" a este associado. A data de referência para a celebração é 11 de março (tabela); somando, inclusivamente 12 (dias) a 11 de março chegamos à data de 22 de março. Sabendo pela tabela correspondente que o regular solar deste mês (março) é 5 e o concurrente anual é 6 (pois o nº de ordem no ciclo solar é 11, ver procedimento infra), saberemos o dia da semana: 5+6=11. Excedendo 7 (limite da sequência de concurrentes), subtrai-se 7 e o resultado é 4. Este dia está associado na tabela dos dias da semana à quarta-feira, e assinala aqui o 1º dia do mês. Logo, "construindo" o calendário do mês, o domingo procurado após o término de 22 de março será o dia 26 de março (que é a Páscoa Ortodoxa, porque estamos a trabalhar no contexto do Calendário "Antigo", Juliano). - Verificar: listagem de datas 2001-2100, em Inglês, inclui o chamado "estilo antigo", v. coluna "Ortodox" a negrito (fonte: http://5ko.free.fr/en/easter.php). - Podemos utilizar o regular pascal (v. tabela que relaciona este parâmetro c/ o nº de ordem no ciclo decemnovennalis, supra) somado ao concurrente anual para verificar o dia da semana do terminus, data da Lua Cheia Eclesiástica: 6+5=11; 11-7=4 (quarta-feira). - Outra verificação complementar pode utilizar somente o concurrente que, como vimos, revela o dia da semana da data 24 de março: 6 equivale a sexta-feira. Comparar com datas relevantes encontradas (22 e 26 de março). (Para saber o nº de ordem no ciclo solar de 28 anos: ano dado + 9; divide-se por 28; o resto é o nº de ordem procurado, não havendo resto será 28) |
Estes venerados métodos revestiam-se de estatuto e gravitas (porque, ao modo "livresco" medieval, a sua instituição é atribuída a outrém mais prestigioso, estabelecidos no contexto niceno ou até angelicamente revelados a S. Pachomius).
A tentativa de publicar informação calendarizada acessível, cobrindo datas recorrentes, acerca da idade da Lua (e.g. os novilúnios), levou à utilização de um sistema de litterae lunares. As que correspondiam às datas no intervalo possível para a celebração da Páscoa eram chamadas litterae paschalis. O sistema das litterae punctatae definia cada dia do calendário (juliano) segundo o ciclo lunar, assumindo, na forma mais comum, uma sequência recorrente de 59 dias (um mês completo de 30 dias mais um incompleto, de 29 dias) repartida em três séries. Os primeiros 20 dias eram representados pela sequência de letras de A a V , os próximos 20 com as mesmas letras seguidas de um ponto (e.g. "A."), os restantes 19 pelas letras de A a T antecedidas de um ponto (da utilização dos pontos deriva o nome do sistema).
| Data | Letra | Data | Letra |
| 1 jan. | A | 1 jul. | E |
| 20 jan. | V | 1 ago. | Q. |
| 21 jan. | A. | 1 set. | H |
| 9 fev. | V. | 1 out. | S. |
| 10 fev. | .A | 1 nov. | K |
| 28 fev. | .T | 1 dez. | V. |
| 1 mar. | A | 2 dez. | .A |
| 1 abr. | M. | 20 dez. | .T |
| 1 mai. | C | 21 dez. | A |
| 1 jun. | O. | 31 dez. | L |
(fonte: Sickel, Theodor, Die Lunarbuchstaben in den Kalendarien des Mittelalters, 1861: 159; tabela completa em Wallis, Op cit., 72)
Todavia, neste procedimento (e também nos regulares feriales), verificava-se o problema dos anos embolísmicos (com 13 meses lunares, ver anotações) e dos anos bissextos. Em ambos os casos acontecem pelo menos dois meses lunares seguidos de 30 dias, subvertendo a alternância dos meses plenos e incompletos. Quanto aos anos embolísmicos, estavam em causa os VIII, XI e XIX do ciclo. O facto de o problema estar confinado somente a três dos sete anos embolísmicos deve-se, segundo Beda, à inteligente organização das intercalações, que o autor atribui aos "Romanos". Philipp Nothaft considera mais plausível que tenham sido computistas insulares, com posterior influência nas regiões Francas, a otimizar o legado da tabela de Dionysius (2018: 55).
O sistema de letras será gradualmente substituído, a partir do século XII, pela referência numérica ao ano dentro do ciclo de 19 (o Áureo Número), incluída nos calendários e marcando as datas do 1º dia da lunação. O método, popularizado por autores como Abão de Fleury (Abbo Floriacensis) ou o didático Alexandre de Villedieu (Villa Dei), ganhará um estatuto pivotal, promovendo a normalização do calendário lunar eclesiástico. Os 235 áureos números, dispostos nos calendários, representam esse mesmo número de meses lunares no ciclo alexandrino de dezanove anos (ver tabela perpétua com os Àureos Números no Calendário Juliano).
MS 17 - Fol. 13v; incipit: Computus tam grecorum quam latinorum et egyptiorum ceterorumque (Abadia de Thorney, Cambridgeshire, ca. 1110; OXFORD, ST JOHN'S COLLEGE); clicar para abrir, JPG, 2,55MB.
- À direita das "Claves Terminorum" está a lista dos 19 anos do ciclo "lunaris". À esquerda das "Claves", na coluna das "litterae punctatae" (“littere lune”) está a correspondente lista dos 19 anos do chamado “Ciclo Pascal” de dezanove, o ciclo "decemnovennalis". Este começa no ano XVII do "lunaris" (cuja função mais óbvia seria conhecer a epacta no dia 1 de janeiro). Este magnífico fólio inclui ainda a relação dos restantes parâmetros fundamentais utilizados na época (regularis, concurrens etc.)
Notas sobre a Epacta em Dionysius et al.
As listagens adotadas e expandidas por Exiguus permitem que o valor da epacta ascenda a 30. Neste caso, o autor subtrai 30 a esse máximo e declara a epacta como nulla (tornando-se um dos primeiros a utilizar um precursor do 'zero', uma vez que não existia numeral para este conceito indo-árabe posterior). Teoricamente, a epacta dita nulla representa o novilúnio, a conjunção com o Sol. A epacta 1 representa a primeira visibilidade teórica do crescente lunar. sendo a partir deste ponto (enquanto 1º dia) que o 14º dia da Lua é contado.
Já vimos que há uma diferença de cerca de 11 dias entre o ano solar (aproximadamente 365 dias) e o lunar (12 lunações, cerca de 354 dias). Ao longo de um trajeto de 19 anos do ciclo, a epacta avançará 19 x 11 = 209 dias (1 dia a menos do que o múltiplo de 30). Daqui a necessidade de adicionar algures 1 dia ao ciclo (o que virá a acontecer por norma no final do ciclo nas tabelas dos computistas). O modus operandi não obedeceu a uma normalização precoce. Muitos computistas enalteceram as vantagens da colocação no final do ciclo (a acontecer na última lunação de 30 dias de julho, última atendendo ao início do ano alexandrino, em setembro). Assim, a luna 30 (de julho) passa a ser (artificialmente) a luna 1 (novilúnio) da lunação de agosto.
Covém assinalar novamente o caráter convencional destes procedimentos. Hermann de Reichenau, matemático e astrónomo do século XI, na Abbreviatio 36 (ed. Germann 2006: 332), relembrou os seus leitores de que não há saltus ou "embolismos" na natureza. Nos meios mais vanguardistas assiste-se, desde o séc. XII, à distinção entre computus usualis ou vulgaris (o convencional), e naturalis (que procurava traduzir com fidelidade os fenómenos), v. Nothaft, Scandalous Error..., p.72).
Intervalli
Em alguns tratados, mais recentes, encontramos algumas variações através da relacionação do parâmetro de dies concurrentes com a sequência septenária das Letras Dominicais e o Áureo Número. Estabelecia-se, para o Ano Litúrgico, a existência de dois "intervalos": Intervallum majus, semanas entre o primeiro domingo após o Pentecostes e o primeiro domingo do Advento; Intervallum minus, o tempo entre o Natal e o sétimo domingo antes da Páscoa (Quinquagésima, sendo 'Esto mihi' o intróito da Missa).
Neste último período verificava-se o nº de semanas (hebdomades) completas. Os dias que sobejavam constituiam um parâmetro do cômputo desse ano, servindo a determinação das datas das celebrações "móveis". Por aritmética ou tabela, determinava-se o parâmetro variável (definido, segundo o "Computus" publicado em 1539 que inclui a seguinte tabela circular, como a contagem inclusiva do nº de dias entre o Natal e o domingo sequente). A "figura" apresenta a relacionação do Áureo Número (de 1 a 19 na periferia exterior) e da Letra Dominical (de A a G) com o parâmetro a utilizar (concurrens, já com utilização do 'zero', sequência de 0 a 6), à esquerda das letras dominicais com as quais têm relação direta. Disponibiliza, no restante esquema, o nº de semanas completas.
Computus ecclesiasticus in pueriles quaestiones redactus..., Ioanne Spangebergio, Vitebergae: Apud Georgium Rhau, 1539; e.g., um ano com Áureo Número 2 e Letra Dominical "E" terá um intervallum com 6 semanas completas, sobejando 4 dies, os parâmetros procurados.
Tabelas complementares registavam as datas "móveis" pré-calculadas para cada combinação destes parâmetros, acautelando anos comuns e anos bissextos (na sequência "juliana").
Excerto de tabela com as datas das celebrações, relacionando as combinações dos parâmetros de semanas (Hebd.) e dias (Dies.), in Computus Theorico-Practicus, facili ac succincta methodo, Christophori Schultz, Bratislava, 1694.
A Letra Dominical baseia-se provavelmente no hábito romano de associar sequencialmente letras aos dias da semana. Os Romanos instauraram o Nundinum, um período de 8 dias independente dos meses/dias num ciclo assinalando os dias de mercado, identificando cada dia com uma letra de "A" a "H". Prevaleceu todavia uma combinação da semana de sete dias e início ao sábado (com origem na astrologia helenística, dias associados aos deuses planetários) com o legado judaico-cristão que obviamente privilegia o domingo como referência pivotal (Holford-Strevens, 2005: 64).
A Letra Dominical reflete o ciclo solar de 28 anos já referido (7 x 4; 7 dias da semana, 4 anos de intervalo entre anos bissextos). Nos livros litúrgicos são assinaladas aos 7 primeiros dias do ano as 7 primeiras letras do alfabeto latino, que se repetem na mesma ordem durante todo o ano. Este sistema estabelece sequencialmente para todos os dias do ano a série retrógrada invariável de letras A,G,F,E,D,C,B (de domingo a sábado), por vezes reservando somente a maiúscula para o "A". A imagem acima inclui mnemónica.

Esquema para determinação da Letra Dominical (partindo do ano de 1512), contemplando também os bissextos, "rotula" com Áureos Números e outra traduzindo o ciclo da Indicção Romana; Petrus (Cracoviensis): Computus novus [et] ecclesiasticus totius fere Astronomie fundamentu[m] pulcherrimum co[n]tinens, clerico no[n] minus utilis qua[m] necessarius ; cum additionibus quibusdam noviter apressis, Vienne Pannonie, 1513
A letra referente ao primeiro dia do ano é fundamental (ver tabela aplicável ao Calendário Gregoriano), definindo o dia da semana em causa. Na prática, permite a construção de todo o calendário, situando especificamente os domingos (daí o nome). Os anos bissextos possuem duas letras, a primeira servindo janeiro e fevereiro, a segunda os restantes meses. O ano diz-se “bissexto” dado o uso convencional de intercalar um “segundo” dia 24 nesse mês, cuja "versatilidade" é antiga, tendo sido reduzido para somente 28 dias para que o romano Sextilis, rebatizado Augustus, pudesse ter 31 dias (Richmond, B, Time Measurement and Calendar Construction, Leiden, E. J. Brill, 1956: 92). Na sequência desta alteração Imperial, o tamanho em dias dos meses seguintes, de setembro a dezembro, foi também invertido.
Na notação romana, perpetuada pela Igreja, o dia extraordinário é o sexto das Calendas de março. Atendendo a que a data da Páscoa deve situar-se entre 22 de março e 25 de abril (inclusivamente), a segunda letra dominical é fundamental em caso de ano bissexto. Segundo Ribeiro (Op cit., 38), "nos anos bissextos o dia 25 de Fevereiro se reputa ter no Calendário a mesma Dominical que o dia 24".
Anos bissextos - resumo das regras gregorianas, implementadas após a "correção":
- São bissextos todos os anos múltiplos de 400, e.g. 1600, 2000, 2400, 2800...
- São bissextos todos os múltiplos de 4, exceto se for múltiplo de 100 mas não de 400
- Não são bissextos todos os demais anos.
As correções solares fazem com que no nosso Calendário Gregoriano o ritmo das Letras Dominicais difira em relação ao ciclo de 28 anos julianos. No antigo calendário, as Letras Dominicais podiam simplesmente determinar-se em função do nº de ordem no ciclo solar de vinte e oito anos, de modo perpétuo:
Letras Dominicais julianas perpétuas, in Computus Ecclesiasticus sive Tratactus Chronologicus, Geiger F., Mannheim, 1731
No novo calendário, a complexidade faz com que a sequência da repetição cíclica das datas da Páscoa se estenda por 5.700.000 anos (e não os 532 anos julianos).
"Repartida a quantidade de hum anno qualquer por 15 , e accrescentando ao residuo 3, (porque ao anno 1.° da era Christã corresponde a Indicção 4 ) teremos a Indicção Romana” (Ribeiro, Op cit., 34)
A Indicção Romana não está relacionada com o cômputo, somente com a cronologia. Remanescente do Império, surge nas antigas Tabelas Pascais (ver supra). O Missal tradicional integra uma tabela perpétua deste ciclo de 15 anos, utilizado, segundo a definição convencional, nas bulas Papais, documentos públicos ou diplomáticos. Atribuída na modalidade definitiva a Constantinus Augustus (Constantino I, o grande cristianizador do Calendário, concomitantemente pontífice máximo da religião romana e do mitraísmo), é mais antiga e foi acima de tudo utilizada para efeitos de tributação (Indictio Tributaria). Segundo Neugebauer, foi introduzida por Diocleciano:
"As is well known, this parameter refers to a 15-year cycle introduced by Diocletian for administrative purposes. But somehow this number acquired the role of a short-term era, frequently used in all kinds of documents from Byzantine domains to the medieval West." (Astronomy and History Selected Essays, Springer Science+Business Media, 1983, p.536)
Na imagem acima, a sequência com início em 1582, anno correctionis, 10 sendo o número de ordem no ciclo.
O cap. VIII das Dissertações... refere três "indicções": a Constantinopolitana, anterior á Justiniana, que principia no 1° de setembro, a Imperial, Constantiniana, ou Cesariana, que parte de 24 de setembro e a Romana, ou Pontifical, que parte de 25 de dezembro, e mais ordinariamente do 1° de janeiro, que prevaleceu (Ibid, 33).
Em resumo, a Indicção chamada "romana" seguia o início do ano (1 de Janeiro ou 25 de Dezembro, entre outros estilos implementados). A original começava a 1 de Setembro.
Listagens dos decisivos e importantíssimos Terminus Paschalis (um para cada ano do ciclo decemnovennalis) estavam disponíveis de longa data, assumindo até a estrutura poética com versos para facilitar a memorização. Faltaria saber o dia da semana em causa, bastando para isso utilizar um regular ferial (também chamado Pascal) associado ao concurrente (v. supra) para determinar o dia da semana do plenilúnio e a data da celebração. Entretanto, tornou-se comum utilizar tabelas para determinação da data da Páscoa recorrendo à Letra Dominical (preterindo os concurrentes, mais antigos e favorecidos pelos cristãos orientais) e obviamente ao Áureo Número (nº de ordem no ciclo).
Este terminus é a data (mínima) limite, na prática a data da Lua Cheia Eclesiástica, luna decimaquarta (ver Limites). O domingo seguinte era encontrado a partir da diferença em dias entre a Letra Dominical tabulada e a Letra do ano em causa (que assinala os domingos), assumindo a sequência invariável: A - domingo, G - segunda, F - terça, E - quarta, D - quinta, C - sexta, B - sábado.
Computus Theorico-Practicus, facili ac succincta methodo, Christophori Schultz, Bratislava, 1694.
(Cf. tabela que inclui as epactas, in Nothaft, 2014: 36)
Utiliza-se Áureo Número e Letra Dominical do ano em causa. Achando a data, verifica-se a Letra Dominical a esta associada na tabela. A diferença entre esta e a Dominical do ano em causa permite saber a data da Páscoa. Exemplo: A.D. 1673 (Áureo Número 2, Letra Dominical E); pela tabela, o término, i.e., luna 14, é no dia 25 de março, sendo "G" a Letra associada. Ora, seguindo a sequência correta das letras (G,A,B,C,D... E), chegamos à data de 30 de março (Páscoa, no Calendário Juliano).
No Calendário Gregoriano utilizar-se-á o novo Cyclus Epactarum e a cadência dos bissextos é, segundo as regras já descritas, muito mais complexa. Uma tabela serviria apenas para determinado intervalo de datas. Os términos continuam a ser os dias da luna decimaquarta (Lua Cheia Pascal, relacionada com a Lua Nova Eclesiástica). A Epacta torna-se o elemento central. No "novo estilo", os calendários publicados passaram também a utilizar as epactas em vez dos áureos números para dar a conhecer a "idade" da Lua, "diretamente", para todos os dias do ano, v. Missale Romanum.
O método adaptado ao Calendário Juliano evoluiu, como vimos, para a utilização concomitante do Áureo Número e da Letra Dominical. Este serve qualquer data anterior à reforma gregoriana e é ainda hoje utilizado pela Igreja Ortodoxa. A partir do Áureo Número calcula-se, com recurso tradicional a tabelas, a Lua Nova Pascal que cai a 8 de março ou após essa data. Somados 13 dias, determina-se facilmente a data da Lua Cheia Pascal. Recorrendo às letras dominicais (cuja tabela é diferente da gregoriana pois utiliza o "antigo" ciclo dos bissextos regulares do Calendário Juliano, menos complexo), situa-se, a partir da Letra associada a esse ano, o domingo sequente, data da celebração Pascal (ver tabelas).
A REFORMA GREGORIANA DO CALENDÁRIO
Gregorius XIII, gravura atribuída a Esaias van Hulsen (Eiulsius) |
Já foi interpretada como um triunfo científico ou como um vetor da afirmação tridentina do poder Papal no contexto da Contrarreforma. Esteve rodeada de polémica, política e críticas ao "desenho" adotado, promovendo argumentações prolixas. Na realidade, com o desenrolar dos séculos, verificou-se o gradual desfasamento entre os cálculos convencionais e a realidade astronómica. Aquando da realização do Concílio de Trento (1545-1563), 1220 anos haviam decorrido desde Niceia. O erro acumulado ascendia a quase 10 dias devido à discrepância entre o ano Juliano e o ano tropical astronómico (1 dia em cada 128,2 anos). Em 24 de fevereiro de 1582 o Papa Gregório XIII publica a bula Inter gravissimas... (i.e. "entre os [assuntos] mais sérios"). Como preconizado, omitem-se os 10 dias entre 5 e 14 de outubro desse ano, declara-se que três em cada quatro anos centenares serão comuns e não bissextos e institui-se um novo Ciclo das Epactas (Cyclus Epactarum). Após a reforma, baseada no desenho de Aloysius Lilius e do jesuíta Bamberguense Christophorus Clavius do Collegio Romano (cuja alma mater foi a Universidade de Coimbra), para além da nova intercalação dos bissextos, o cálculo do domingo de Páscoa e das outras festas móveis dependentes encontra-se através de tabelas que entram em linha de conta com as mudanças trazidas pela nova utilização das Epactas e com os ajustamentos dinâmicos, antecipadamente previstos no desenho da correção. É o que vamos procurar expor. |
Para além do referido desfasamento que acumulou quase 10 dias, havia a limitação inerente à implementação metónica. João P. Ribeiro, Op cit., 36) resume este desfasamento lunar:
"Comtudo a experiencia mostrou, que a differença de 19 annos Solares aos Lunares era mais que os 7 mezes Lunares (intercalados nos 7 annos embolismicos deste Cyclo) 1h 27' 31" 55", de sorte que desde o anno de 325, em que se célebrou o Concilio Niceno (que por elle regulou os Novilunios), até o anno de 1582 da Correcção Gregoriana, em menos de XI. Seculos, se tinha errado em 4 dias: tanto se tinha adiantado o Aureo numero, marcando já não o 1.°; mas o 5.° dia da Lua; pois aquella hora, e minutos em 312 annos e meio equivalem a hum dia. A [nova] Epacta se adoptou naquella Correcção, para precaver este engano, e para se achar esta he que sómente se conservou o Aureo numero no Kalendario reformado."
Antes do pontificado de Gregório XIII (nasc. Ugo Buoncompagni), Pio V (falecido em 1572) havia publicado (1568) um renovado Breviário que apensava uma reforma provisional do calendário (que recuava ou antecipava os Áureos Números 4 lugares), todavia com discrepâncias e sem sucesso. Clavius reconhece em Luigi Giglio (Lat. Aloysius Lilius) o principal autor da reforma, nomeadamente através do novo Ciclo das Epactas. Conhecemos a sua influência indirectamente, principalmente a partir do Compendium novae rationis restituendi kalendarium, um sumário com as novas propostas (editado pela Comissão responsável), dirigido principalmente ao peritis mathematicis e que foi colocado a circular nas regiões Católicas. Com modificações, o seu desenho está na base do calendário renovado. Como A. Ziggelaar explicou (e aqui resumimos), doravante a epacta do ano, o número adicionado à idade da Lua, torna-se a base para determinar a sua "idade" para qualquer dia no ano solar. A Epacta era a idade da Lua no início do ano solar e também o número de dias que sobejavam no ano transato depois da última lunação. Antes era unicamente determinada pelo Áureo Número, de modo direto e inamovível e, com a ajuda da Letra Dominical [ou de qualquer outro expediente para conhecer a feria, o dia da semana], permitia localizar o domingo da Páscoa. Mas com a passagem dos séculos, os mencionados números deixaram de cumprir a sua importante função e já não determinavam as epactas, i.e. a "idade da Lua", com rigor. Por exemplo, se o Aúreo Número fosse 7 a Epacta seria XIV, mas na realidade já era XVII na época de Gregório XIII. Giglio (Lilius) deu o passo decisivo e quebrou a antiga relação fixa. Doravante, no decorrer dos séculos, um dado Áureo Número (que pertence a uma sequência fixa de 19) pode relacionar-se com qualquer das trinta possíveis epactas. Consequentemente, no calendário perpétuo, a cada data é associada uma Epacta e não um Áureo Número. Se a Epacta de um determinado ano for V, todas as datas desse ano com essa mesma Epacta serão dias de novilúnio, i.e. Lua Nova (v. tabela perpétua). As séries das epactas têm de ser alteradas amiudadamente (quase todos os séculos) para serem aplicados os ajustamentos (lunares e solares) que garantem o bom funcionamento. Para o ajustamento solar, Giglio seguiu Pietro Pitati de Verona, que havia sugerido deixar de fora o bissexto nos anos centenares não divisíveis por 400. O procedimento perturba o Ciclo Metónico, de modo que a Lua se atrasa um dia sempre que se aplica. O inverso acontece quando similarmente se ajusta o movimento da Lua: após um Ciclo Metónico de 19 anos, a Lua antecipa as suas fases 1 dia em 312,7 anos (8 dias em 2500 anos). Giglio corrige aumentando as epactas em uma unidade a cada 300 anos e uma oitava e última vez após 400 anos. Por fim, era necessário corrigir definitivamente o erro acumulado na data do Equinócio (que de 21 havia recuado para 11 de março) desde a época do Concílio de Niceia. Suprimiram-se 10 dias e "saltou-se" para a linha correcta das epactas. (The Decree of 1582, in: Coyne, G. V., Hoskin, M. A. and Pedersen, O. (eds.), "Gregorian Reform of the Calendar Proceedings of the Vatican Conference to Commemorate Its 400th Anniversary, 1582-1982", Pontificia Academia Scientiarvm, 1983: 210-11 [trad. nossa]), A Comissão responsável escolheu Outubro para a supressão dos dias porque, segundo Clavius, a perturbação seria menor pois há menos festas de santos nesse mês (Romani Calendarii a Gregorio XIII. P.M. Restituti Explicatio; ...Operum Mathematicorum Tomus Quintus, Mainz, 1612 (ed. princeps 1603), 66).
Antecedentes
Com a passagem do estilo monástico para a implementação do saber escolástico no século XII, com a reorganização do ensino (universidades) e o acesso a um maior acervo de autores (antigos e coevos), novas sensibilidades vão surgindo. As críticas ao funcionamento do calendário são evidentes quando se trata dos que advogam o computus naturalis e o sequente computus philosophicus (do nome de alguns dos tratados), no século XIII, respondendo à evolução do conhecimento astronómico, nomeadamente pela integração da ciência dos árabes (Nothaft, 2018, 125 et seq.), instrumentação e tabelas astronómicas cada vez mais precisas.
Ainda no século XI se pode documentar o Computus emendatus de Reinher de Paderborn (c. 1171), que defendeu a utilização do molad judaico (ver enquadramento deste interesse por Philipp Nothaft, in Journal of Jewish Studies 65(1):148-168 - March 2014). Entre outros críticos, o anónimo ‘Liber decennalis in modum dialogi compositus’ (Bibl. Angelica, Roma. MS 1413, ff. 1 – 24) e Roger Bacon, o Doctor Mirabilis, que na Opus Majus (enviada ao Papa Cemente IV em 1267), sugeriu uma alteração do calendário. Os desfasamentos eram até desvelados por métodos populares ou empíricos, regula rusticorum.
Bacon foi assertivo: [Kalendarium] est intolerabilis omni sapiente, et horribilis omni astronomo et derisibilis ab omni computista (Op. ter. cap. I xvii).
A resistência à mudança e o peso dos "ditames" nicenos fez-se sentir. Para quem conhecesse a letra dos antigos textos epistolares, conciliares e canónicos, a antiga ameaça de excomunhão (supostamente emanada de um concílio realizado em Antioquia) para quem desses princípios se afastasse em questões pascais, seria dissuasora (Dionysius Exiguus, Epistola ad Petronium, ed. Krusch, 1938: 66-7, ver).
Uma proposta veemente foi apresentada ao Concílio de Basileia (iniciado em 1431) por Hermann Zoest. Este pretendia reescrever o ciclo dos Áureos Números, respaldado nas Tábuas Afonsinas, convencionando um novo início imediatamente em 1425, com o novilúnio de janeiro no dia 19 e calculando de acordo com este os restantes 234 do cyclus (Nothaft, 2018: 251). A tentativa não sucedeu, invocadas as perturbações na deslocação exigida dos términos pascais (intervalo de datas onde a Páscoa pode situar-se), bem como as alterações necessárias nos breviários, tabelas e tratados, pois tratar-se-ia de uma nova sequência.
Entretanto, Nicolau de Cusa (Nicolaus Cusanus, 1401-1464) apresentou uma proposta (De correctione kalendarii) que visava "voltar" aos tempos nicenos. Para isto pretendia converter a interpretação dos Áureos Números para o "cyclus lunaris" (em detrimento do decemnovennalis) e omitir uma semana no calendário para corrigir o óbvio desfasamento. Mas a agilização da reforma ainda aguardaria, o tema só foi indiretamente reaberto com autoridade na última sessão do Concíclio de Trento, a propósito da revisão dos livros canónicos, missal e breviário (Holford-Strevens, 2005: 35).
Em definitivo, e em termos técnicos, a supressão de dias não bastaria para reconciliar o cômputo pascal com a astronomia. Mas a diferença entre o equinócio nominal e o real foi a motivação fundamental para a reforma (Holford-Strevens, Op cit., 35). Seria fundamental restaurar o equinócio para a data de 21 de março (que se acreditava erradamente ter sido um ditame niceno). Com os ajustamentos criados reconcilia-se o calendário lunar com a Lua e a luna (fase/"idade") para qualquer data é doravante achada através da epacta, na sua nova modalidade.
A receção do calendário renovado
O
acolhimento foi evidentemente condicionado pela política
e pelo sectarismo religioso. Nas Igrejas reformadas do centro e norte da Europa, era comum o
argumento de que as deliberações do Concílio Geral de Niceia não podiam
ser alteradas pelo Tridentino, que ao contrário do prestigioso exemplo
mencionado, não reuniu toda a Cristandade, sendo exclusivamente
Católico Romano. Do lado Católico surgiram críticas a determinados
detalhes técnicos, bem como discussões (por vezes acesas, e.g., entre Scaliger e Clavius), sugestões e propostas (e.g.,
Scaliger, Calvisius, Vieta, que até publicou a "sua" versão). Do lado Protestante, apesar da
alargada consciência da relevância e necessidade da correção (historicamente bem patente),
prevaleceu um antagonismo 'extra-científico', i.e. político e/ou religioso. Entre os mais "ferozes", Michael Maestlin, por exemplo (Außführlicher Bericht von dem allgemynen Kalender...,
Heidelberg, 1583), declara que o Papa não tinha o direito de instituir
uma reforma e considera-o mesmo um "herético", pois ao falar de Calendarium perpetuum ("Calendário perpétuo") manifesta (tal como os autores dos Canones)
a descrença no Juízo Final, que Maestlin acreditava estar próximo.
Jacobus Heerbrand, da Universidade de Tubinga, afirmou, no Disputatio de Adiaphoris et Calendario Gregoriano (Tubingae, 1584) que o Papa era o Anticristo (opinião comum na retórica protestante), o Gregorius Calendarifex que... putavisse posse mutare tempora ("pensava que podia mudar o tempo!"). E o calendário foi até comparado
ao 'Cavalo de Tróia'. Outra questão era a da relação entre fé e
ciência. A perspectiva prevalecente na Universidade de Paris era a de
que a reforma não deveria ser colocada sob a responsabilidade de
astrónomos, a não ser que se pretendesse substituir os ciclos
eclesiásticos pelos astronómicos (o que não era o caso nem seria
exequível com o rigor e universalidade que se almejava, como mais tarde
(c.1700), se verificou em terras Alemãs ao tentar calcular a Páscoa a
partir de tabelas astronómicas, no caso as Rudolphinae
(Rudolfinas)). Mas a própria Cúria Romana manifestava de longa data
algum desconforto
perante a "dependência" da Astronomia. No que a esta disciplina diz
respeito, Clavius fez uma defesa competente das opções que foram
tomadas, salientando que o recurso aos 'movimentos médios' (do Sol e da
Lua) radicava na ausência de tabelas suficientemente precisas e na
necessidade de agilizar um resultado para a data da Páscoa que fosse
"universal", independente das diferenças de longitude (geográfica).
"Deveriam Lisboa e Catigara (Cantão) celebrar a Páscoa de acordo com os
fenómenos [circunstâncias locais], mesmo que isso significasse fazê-lo
com um desfasamento de oito dias?". A questão foi colocada por Georg
Tanstteter e Andreas Stiborius a partir de Viena, no âmbito do V
Concílio Laterano (i.e. de Latrão, 1512-17, onde esteve o influente
matemático Paulo de Middelburg). Ambos se inclinavam para a opção
"astronómica" mas compreenderam que esta dependeria da geografia.
Entretanto, Johannes Stoffler recorre ao velho argumento entre a
"verdade" (dos fenómenos) e a "ficção" (do cômputo). Mas a verdade
astronómica é sempre 'local'. Que meridiano de referência utilizar?
Roma? A escolha seria sempre polémica. Para a Igreja, as discussões astronómicas e a falta de consenso apenas fortaleceram
os argumentos a favor do ágil sistema esquemático ou convencional,
cientificamente informado mas não estritamente geográfico-astronómico nem
baseado em circunstâncias locais. Trata-se sempre de um compromisso. O
próprio Lilius concedeu que no seu sistema de Epactas, a Páscoa podia
ocasionalmente não "cair" no domingo a seguir à lua astronómica (i.e. real, aparente).
No contexto Ortodoxo, apesar da simpatia manisfestada por Jeremias II Tranos, Patriarca de Constantinopla,
a reforma foi declinada, por vezes vilipendiada, outras ignorada. As
circunstâncias políticas, a desconfiança mútua, o "nervosismo"
por parte do poder Turco, a ausência de poder efectivo por parte do
Patriarca (ao contrário do que acontecia no "monarqusmo" Romano) e,
apesar das sigilosas conversações em curso, a instituição unilateral do
novo calendário por parte do Papa, nada contribuiu para a causa
ecuménica. Noutros países, a
reforma foi defendida pelo astrónomo Ole Roemer na Dinamarca, por
Leibnitz na Alemanha e por John Dee na Inglaterra Isabelina. Neste
último país, bem mais tarde e aquando da adoção do chamado "New Style"
(N.S.) em 1752, o Reverendo Peirson Lloyd (no sermão The new style the true style,
1753: 27) chamou a atenção para o absurdo que seria, com o transcorrer
do tempo e o desfasamento a acumular-se, se um dia futuro
as celebrações do Natal e da Páscoa viessem a ser observadas no mesmo
dia! Se nada fosse feito, aconteceria mais cedo ou mais tarde. Na
Rússia, o Calendário Gregoriano só foi adoptada (pelos
Bolcheviques) em 1918, aqui curiosamente também (mas não
exclusivamente) como desafio anti-clerical em relação à Igreja
Ortodoxa. O novo sistema tornou-se gradualmente universal, por diversas
razões, nomeadamente económicas, financeiras e diplomáticas,
tornando-se, na prática, o sistema internacional secularizado. Está longe de
constituir uma gestão puramente lógica e racional do tempo mas foi
assim que se desenvolveu nas diversas e complexas circunstâncias históricas,
herdeiro de múltiplas influências e tradições, adaptando-se
e funcionando num equilíbrio difícil entre a usabilidade, a
simplicidade, o simbolismo litúrgico e a tradução de ciclos
astronómicos dificilmente redutíveis a soluções simplificadoras e
duradouras no longo prazo. (vide Nobis, H. M., The Reaction of Astronomers to the Gregorian Calendar; Hoskin, M., The Reception of the Calendar by Other Churches e Gingerich, O., The Civil Reception of the Gregorian Calendar; publicados in: "Gregorian Reform of the Calendar Proceedings of the Vatican Conference...", Op. cit., 1983).
As
tabelas gregorianas serão diferentes das julianas: o ciclo solar e a
Letra Dominical devido à nova regra dos anos bissextos ao longo da
quadricentúria e as epactas configuram doravante um Cyclus Epactarum com uma dinâmica muito diferente (v. exemplo comparativo [PDF 95KB], M. Natalis de Wailly, Éléments de Paléographie..., Tome I, Paris, Imprimerie Royale, 1838, p.112).
A Epacta, ou melhor, o novo Cyclus Epactarum, assume a centralidade devido a uma relação dinâmica com o Áureo Número. Como referido, ao contrário do que acontecia no Calendário Juliano, no qual a aplicação era entendida sem alterações e ilimitada, a relação entre Áureo Número e Epacta varia doravante em consequência das equações (solar e lunar). A Epacta assume, no "sistema" gregoriano, trinta valores possíveis, interpretando aproximadamente os dias de uma lunação.
A epacta medieva baseava-se, como vimos (tal como o número áureo),
no Ciclo Metónico. A amplitude do desfasamento no calendário era
evidente, acumulando 8 dias num período de 2500 anos. Foi instituida a
mudança de 1 dia em determinados anos centenares, ajustando o cômputo
da idade da Lua 7 vezes em cada 300 anos e mais 1 vez após os 400 anos
subsequentes ("correcção lunar"). Mas como o novo Calendário Gregoriano
vai utilizar um valor mais preciso para o Ano Tropical, foi necessário
omitir quase todos os anos bissextos centenares e introduzir uma
"correcção solar": quando o novo Ciclo das Epactas
chega a um ano centenar normal, o valor da epacta deve ser reduzido 1
unidade. Para determinar a Páscoa, foi preparada uma tabela com os
dezanove áureos números e os
ciclos epactais para um período de cerca de 7000 anos, após o qual os
ciclos se repetem. Sabendo o valor da epacta, a data da Lua Cheia Pascal era
imediatamente obtida numa segunda tabela que faz corresponder cada
epacta à data do plenilúnio relevante. Bastava então consultar outra
tabela (a das Letras Dominicais) para determnar o próximo domingo: a Páscoa.
Philipp Nothaft (2018: 294) observa argutamente que o esquema de epactas divisado originalmente por Lilius se assemelha ao das antigas litterae punctatae, na medida em que identifica a “idade” da Lua para cada dia do calendário, sem necessidade de qualquer outro expediente.
A Tabula Epactarum expansa de Lilius apresenta as diferentes implementações das epactas (19x30) em função dos ajustamentos (solar e lunar), disponibilizando uma coluna com letras que permitem aplicar (recorrendo a tabela auxiliar, Tabula Aequationis) as correções em função das sequências de dezanove anos. Isto em resposta aos intervalos cronológicos em causa. A epacta inicial (0=30) é indicada como * ou ω (ómega minúsculo). A epacta de Lilius sofre o incremento dos tradicionais 11 dias anuais, exceto no último ano do ciclo, no qual serão 12.
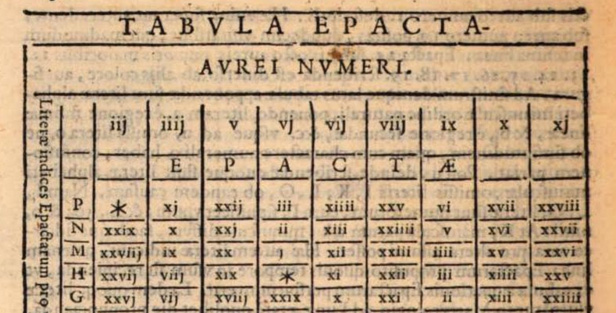
Tabula Epactarum expansa (excerto); inicia com o Áureo Número 3 (iij) quando a epacta é nulla no dia 1 de janeiro; Clavius, Christophoro, Novi Calendarii Romani apologia, adversus Michaelem Maestlinum…, Romae, MDCXXXVIII
O valor raíz, traduzível pelo algarismo zero ou pelo número 30 (nos meses de 29 dias, cavi, incompletos), é quase sempre representado por um símbolo não aritmético: .
Este assinala o novilúnio. Uma epacta equivalente a 13 ("dias",
contados inclusivamente a partir do 1º) está associada ao plenilúnio, luna decimaquarta. A "idade" da Lua é, como sabemos, referida em latim como luna, seguida de numeral.
Em definitivo, as epactas assumirão doravante a função essencial, outrora configurada pelo Áureo Número.
Numa interpretação superficial de um estudo do qual somente conhecemos o abstract (Dekker, Elly, 1993, Epact Tables on Instruments: Their Definition and Use, Annals of Science, 50), não se descarta, todavia, a existência de alternativas pretéritas (anteriores à "correção") ajustadas à natureza (i.e. aos fenómenos), compensando desfasamentos, não no âmbito do cômputo, antes nas vertentes utilitárias quotidianas (náutica, astrologia, iatromathematica, etc.).
Segundo Jacob A. Zallinger (Instititiones Juris Ecclesiastici Maxime Privati Ordine Decretalium, Roma, Collegio Urbano, 1832 , ed. princeps: Augsburg, 1792-3), no Calendário Gregoriano os anos embolísmicos são aqueles cuja epacta anual é igual ou superior a 19, Cujus epacta annua est XIX aut major (Caput VIII, LXIX), pois acumulando o desfasamento de 11 dias, alcança ou ultrapassa o limite que lhe é inerente.
Tivessem os 19 Áureos Números sido perpetuados na indicação dos novilúnios (e não substituídos pelas novas epactas), todos se "deslocariam" 7 dias relativamente ao antigo posicionamento. Assim, por exemplo, o III (que sinalizava o 1º dia de janeiro), estaria fixado no dia 8 desse mês, existindo seis dias de intervalo entre os antigos e os novos 'sítios', o mesmo valendo para todos os restantes números da sequência (Butcher, Op cit., 118). Responder-se-ia ao desfasamento astronómico com a deslocação implícita da outrora inamovível sequência dos Áureos Números.
Após a "correção", assistimos a delongas na adoção e a decisões peculiares. Os luteranos alemães, por exemplo, adotaram o “novo estilo” (em 1699) mas não as tabelas Pascais gregorianas. Optaram pelo chamado calculus astronomicus, seguindo o equinócio verdadeiro e a lua cheia astronómica, recorrendo à melhor informação disponível: as tabelas de Tycho Brahe, produzidas para o meridiano do seu observatório de Uraniborg (Holford-Strevens, Op cit., 60).
A reforma encetada traz para o cômputo uma nova metodologia, plasmada por Clavius nos seus Cânones de 1582 e posterior explanação (Romani calendarii a Gregorio XIII P.M. restituti explicatio. Roma, 1603) Todavia, há o cuidado de manter o carácter cíclico dos procedimentos e sugerir conformidade com os antigos métodos e princípios, o que se manifesta na pedagogia, divulgação e afirmação de que se tratava de uma restitutio do Calendário Romano à sua forma original (Nothaft, 2018: 298). Abandona-se a utilização da localização do Áureo Número de determinado ano na sequência no ciclo decemnovennalis para estabelecer a data das luas eclesiásticas, pois as tabelas e a natureza divergem após um intervalo de cerca de dois séculos. Através do novo Cyclus Epactarum, uma tabela é válida e ajustada para um determinado intervalo de cerca de 3 séculos, sendo substituída por outra e assim sucessivamente. Em resumo, a Epacta ainda é conhecida/calculada a partir do Áureo Número mas em função de/ou para determinado ano específico, devido às correções entretanto introduzidas (disponibilizam-se tabelas válidas para determinado intervalo).
|
"CHRISTOPHORVS CLAVIVS BAMBERGENSIS" (gravura a partir de pintura de Franciscus Villamoena, Roma, 1606) |
Correspondência do Áureo Número com a Epacta para o intervalo de 1900 (incl.) a 2200 (excl.), segundo o Missale Romanum, editio XXXI post typicam, Roma, 1911
A epacta para determinado ano (no seu 1º dia de janeiro) é, por norma, 11 valores superior à do ano precedente (os omnipresentes 11 dias de desfasamento lunar-solar). Se o total ultrapassar 30, subtrai-se esse mesmo valor. Assumem, como referido, 30 valores possíveis e a cada dia corresponde uma das trinta epactas. O Calendário disponibilizado no Missale Romanum tradicional exibe o Cyclus Epactarum em pequenos números romanos. A epacta registada corresponde ao dia do mês (Dies Mensis) apontado na quarta coluna, no qual a Lua Nova cai em determinado ano. É, na prática, uma tabela perpétua. Permite determinar as "idades"/fases da Lua, sabendo o valor correspondente à Epacta desse ano. Todavia, apesar do exarado no 2º Cânone da Reforma (Epacta nihil aliud est quam numerus dierum quibus annus solaris communis dierum 365 annum communem lunarem dierum 354 superat), afirmando a tradicional definição do excesso de dias do ano solar relativamente ao lunar, a Epacta já não pode, por via das correções, ser exata e tecnicamente interpretada como representando "dias", tornando-se mais "teorética" e afastando-se da relacionação metónica do passado. Ver tabela perpétua e anotações relacionadas com o "posicionamento" das epactas.
Ajustamentos implementados: uma Equação Solar, reduzindo 1 dia à epacta sempre que o calendário ignora um ano bissexto (3 vezes em cada 400 anos) e uma Equação Lunar, aumentando 1 dia à epacta 8 vezes em 2500 anos do calendário (7 vezes após um intervalo de 300 e a 8ª após um intervalo de 400 anos).
A grande vantagem do sistema (epactas) é a determinação das lunações para todo o ano e, obviamente, da Lua Nova Eclesiástica (ver tabela), Lua Cheia Pascal e data do Domingo da Páscoa, somente subtraindo e adicionando. Embora se utilize o Áureo Número para saber a Epacta, basta o valor da Epacta (para determinado ano) para encontrar a data da Lua Nova Eclesiástica, subtraindo-o ao valor 31 (março tem 31 dias). Somando 13 dias ao resultado obtemos a data da Lua Cheia Pascal. A Páscoa é no domingo seguinte.
Ajustamentos ao Cyclus Epactarum
Doravante, a cada 30 dias do mês lunar "normal" correspondem 30 epactas. No Calendário Gregoriano surgiu o problema da atribuição das epactas xxiv e xxv ao mesmo dia nos meses lunares mais pequenos (cavi, de somente 29 dias). Isto criou um problema novo que faria o ciclo “fechar”, de modo "desarmonioso", antes de se cumprirem os 19 anos da sequência metónica. De modo a impedir, por regra, que a data da Lua Eclesiástica se repita dentro do mesmo ciclo, criou-se um estratagema: sempre que as epactas xxix e xxv acontecem no mesmo ciclo, as Luas Novas de um ano com epacta xxv passam a xxvi. A "nova" epacta criada aparece também por vezes como 25’, devendo ser lida como "26" nos meses lunares de 29 dias. Em resumo: xxv e 25 distinguem-se pois as fases da Lua não podem, ou não devem, repetir-se nas mesmas datas dentro do mesmo ciclo. Ver aequationes e o cálculo através de fórmulas que utilizam e "corrigem" a epacta antiga.
Tradicionalmente, quando um ano apresenta xxv como valor da epacta, utilizam-se nas tabelas os valores 25/xxv (numeração árabe/numeração romana) em função do valor do Áureo Número, usando a epacta “25” se Áureo Número for igual ou superior a 12 unidades e “xxv” (ou cor vermelha, "rubeo tincta colore" diferenciadora) se menor do que 12 (as tabelas acautelam devidamente os ajustamentos).
Thesaurus Sacrorum Rituum: Continens Ordinem Perpetuum & Generalem recitandi Divini Officini, Gavanti vitam, & Indices Auctorum, quibus uterque Auctor usus est, Volume 2, Edição 2, Salvioni, Roma, 1738
Isto apesar da confusão em alguma bibliografia, invertendo amiudadamente o procedimento. Um exemplo paradigmático ocorreu em 1734 (Epacta xxv, Áureo Número 6 e Letra Dominical "C"), referido no Compendio metódico y claro del Cómputo, de Don Pedro del Rio (editado em Madrid em 1790) e no Thesaurus acima aduzido, ambos esclarecedores quanto ao procedimento. Por não ser acautelada a regra supracitada, houve lugar a equívocos na determinação da data da Páscoa segundo as tabelas de alguns breviários e missais. A data que prevaleceu foi obviamente a correta, 25 de abril (ver tabela).
Muitas edições da Tabella Paschalis nova reformata ("derradeira" tabela que relaciona Letra Dominical e Epacta para saber as datas das chamadas "Festas Móveis" de determinado ano) optam pela utilização exclusiva da numeração árabe, recorrendo à cor, negrito ou acentuação (25') para diferenciar o "duplo" 25 (vide epacta servida pelo Áureo Número igual ou superior a 12 destacada a negro neste excerto; clicar para versão completa em formato PDF, 70KB). Esta tabela inclui as celebrações relacionadas, por ordem cronológica: Septuagesima, Dies Cinerum, Pascha, Ascensio, Corpus Christi, Pentecostes, (Dom. post. Pent.) e Dom. prima Advent. (designações latinas tradicionais).
MISSALE ROMANUM, REIMPRESSIO EDITIONIS XXVIII. JUXTA TYPICAM VATICANAM. BONNÆ AD RHENUM - ÆDIBUS PALMARUM MMIV
(Ver tabela Festas Móveis equivalente.)
Achar os novilúnios e a "idade" da Lua
João Pedro Ribeiro, eclesiástico e canonista nascido em 1758, nas suas Dissertações... (50 et seq.) deixa indicações práticas para determinar pela epacta (de determinado ano) a data do novilúnio de qualquer mês, bem como a idade da Lua para qualquer dia, sem o recurso a tabelas. Trata-se de um processo análogo ao dos antigos regulares. Neste caso, uma soma na qual não se contabilizam as parcelas dos meses de janeiro e março (basta a epacta anual já conhecida), fevereiro corresponde a 1, os outros meses ao nº de unidades contadas desde março, inclusivamente (e.g., para julho será 5).
Achar o novilúnio de qualquer mês. (...) Assim para saber, a quantos de Junho de 1894 cahio o Novilunio, sommo 18 (Epacta do mesmo anno ), com 4 ( numero dos mezes desde março a Junho inclusive): a somma 22 diminuo de 30 , e acho o residuo 8, que mostra, que em Junho foi a Lua nova a 8. (+14 = Lua Cheia) Nos mezes de Janeiro, e março nada se accrescente, e ao de Fevereiro, e Abril uma unidade.
Para achar logo a idade da Lua em qualquer dia determinado, se somma a Epacta desse anno com os dias do mez, e o numero dos mezes desde março inclusive, tirados os 30 sendo necessário. nada se accrescenta a janeiro, e em Fevereiro 1 unidade.
Mais rigorosamente, segundo a 19ª edição do The New Practical Navigator; Being a Complete Epitome of Navigation…, editada em 1814 em Londres por Joseph Dessiou, (p. 124), soma-se a epacta ao dia do mês e ainda a um parâmetro que corresponde a um número, a “epacta do mês”. Determina-se dividindo por 29,5 (dias do mês lunar astronómico), o nº de dias desde o início do ano até à data em causa. O remanescente será o número procurado.
.