
O Ciclo de Dezanove Anos
Considerações gerais, disposição dos Áureos Números na tabela e colocação dos embolismos.
A sequência dos números na tabela perpétua é a seguinte: 3,11,19,8,16,5,13,2,10,18,7,15,4,12,1,9,17,6,14. A distribuição é determinada pelo início do ciclo e pela sequência das lunações, de 30 dias (pleni) e 29 dias (cavi); a cadência de repetição de um número pode ser explicada pelo Oktaeteris, um ciclo de 8 anos solares após o qual um novilúnio cai na mesma data do calendário, com uma diferença de mais 1 ou 2 dias.
- As lunações de 30 dias começam sempre no ano transato (exceto para o ano III, com novilúnio no dia 1 de janeiro); as lunações para cada ano do ciclo (verificadas pelo Áureo Número registado) traduzem um ano lunar; os anos embolísmicos integram 13 lunações, os restantes 12.
Quanto ao desenho, o Áureo Número 3 está fixado no dia 1 de janeiro, indicando o primeiro novilúnio. Sucessiva e alternadamente computa-se 30 e 29 dias (lunações convencionais) ao longo dos meses do ano, justapondo aos dias encontrados o nº 3 até esgotar os 354 dias do ano lunar. Seguidamente, procede-se de modo similar para o Áureo Número 4, fixado de início no dia 20 de janeiro. Somando esta nova parcela (contada a partir da última lunação do Áureo Número 3 até à última do 4), chegamos aos 708 dias previstos, i.e., dois anos lunares. O sistema prossegue até contemplarmos o Áureo Número 2, escoando o total de dias do ciclo (configurando o sistema de lunações convencionais composto por 125 meses completos e 110 incompletos, acumulando 6940 dias).
A estrutura das lunações foi tradicionalmente conseguida respeitando os seguintes critérios:
- A 1ª lunação do ano deverá ter 30 dias e começar no ano precedente
(exceto no início do ciclo, quando os ciclos lunar e solar estão
sincronizados);
- Não deverá existir mais do que um Áureo Número associado a cada dia da tabela (ver exceção infra, pouco explorada na literatura mas tempestiva);
- A lunação pascal deverá ter somente 29 dias;
- As lunações completas e incompletas devem geralmente alternar,
particularmente no início de cada ano (esta última regra nem sempre
pode ser observada).
Agilização...
Os anos "comuns" do ciclo decemnovennalis integram 6 meses lunares completos (30 dias) e 6 incompletos (de 29 dias). Acresce que 6 dos 7 anos embolísmicos podem ter um complemento de lunações de 29 ou 30 dias. Deste modo, (19 X 6 X 29) + (19 X 6 X 30) + (6 X 30) + 29 = 6,935 dias, equivalendo a 19 X 365, o nº de dias do período de 19 anos. Todavia, contando com os bissextos de quatro em quatro anos (19 X 365.25 = 6,939.75 dias), torna-se necessário subtrair (6,939,75 - 6,935 = 4,75 dias). Deste modo, o desenho do ciclo harmoniza-se com o Calendário Juliano.
Os meses extra permitem alcançar as 235 lunações necessárias aos 19 anos solares. Estas intercalações eram alternadas procurando "replicar" a dinâmica dos meses do ano solar. E cada lunação "pertencia" a um mês (solar), o mês em que terminava (In quo completur mensi lunatio detur) ou mensi luna datur cui fine suo sociatur ("A Lua pertence ao mês ao qual se junta no seu final").
Outrora, segundo C. Wheatly (A Rational Illustration of the Book of Common Prayer of the Church of England, Oxford 1794), tendo o ano início em março segundo o antigo costume, permitia-se que a lunação que terminava nesse mês tivesse 30 dias, a de abril 29, a de maio novamente 30, e assim sucessivamente, como se constata nos versos:
Impar luna pari, par fiet in impare mense;
In quo completur mensi lunatio detur.
...pois os meses ímpares têm lunações plenas, de acordo com o cômputo de 30 dias (pares lunae), os meses pares têm lunações incompletas ou desiguais (impares lunae).
.
Anotação sobre a disposição dos Áureos Números na tabela (seguindo a exposição de Philipp Nothaft, 2018: 58 et seq.).
Os 19 anos do ciclo incluem (no enquadramento do calendário Alexandrino) sete (anos lunares) embolísmicos (3º,6º,e 8º, ainda o 11º, 14º, 17º e 19º), por isso o ciclo de 19 foi dividido em ogdoas e endecas (intervalos de 8 anos contendo 3 embolísmicos e 11 anos contendo 4 embolísmicos, respetivamente). Cada lunação embolísmica possui 30 dias, o ano embolísmico possui 13 meses, ou 384 dias, excedendo o ano lunar comum em 30 dias e o solar em 19.
A sequência (verificável na Tabela Perpétua) começa com o Áureo Número 3 no dia 1 de janeiro, identificando o lugar do novilúnio no 3º ano do ciclo decemnovennalis, de 19 anos. O mesmo nº aparece 30 e 59 dias depois (1 mês lunar completo mais 1 incompleto) associado a 31 de janeiro e 1 de março. Janeiro e março apresentam um padrão correspondente na distribuição dos números.
Dos 365 dias do ano juliano comum, 131 estão perpetuamente desprovidos de número (i.e., sem novilúnio no calendário), pois há somente 235 lunações para distribuir. 2 de dezembro é a única data a receber dois Áureos Números (a saber, 2 e 13), por razões que Robertus Grosseteste explanou no seu Compotus correctorius (circa 1220).
Segundo o compotista, o intervalo de 8 anos (referindo-se ao primeiro intervalo da convencional divisão do ciclo entre ogdoas e endecas, de 8 e 11 anos, respetivamente) que separa dois novilúnios que caem no mesmo mês juliano, encompassa, habitualmente, 96 lunações comuns de 29,5 dias e 3 embolísmicas de 30 dias (2832+90=2922 dias). Este valor excede em 2 dias o nº de dias de 8 anos julianos comuns (8x365=2920 dias). Explica-se assim porque é que o Áureo Número 1 é seguido, dois dias depois, pelo Áureo Número 9. Uma alteração acontece quando o intervalo referido inclui o último ano do ciclo. Neste caso, devido ao saltus lunae (ajustamento), o intervalo é reduzido para 2921 dias. Isto explica a razão pela qual os Áureos Números 13 e 2 normalmente se situam em datas adjacentes. Todavia, no caso da referida data de 2 de dezembro, para além do saltus lunae, o mês embolísmico que convencionalmente pertence ao ano XIV do ciclo foi já inserido de facto no ano XIII (com novilúnio no dia 2 de novembro). Deste modo, o nº total de dias do intervalo de 8 anos (ogdoade) é reduzido para somente 2 lunações embolísmicas (30 dias cada) mais 97 comuns, das quais a primeira e a última são incompletas (de 29 dias). Assim, a soma equivale ao mesmo nº de dias do período de 8 anos julianos comuns (2920 dias). Resulta que, no 1º dia do nono ano, a Lua tem novamente 1 dia de “idade”. É por isto que é necessário que dois "novilúnios" (dois Áureos Números) sejam colocados no mesmo dia, 2 de dezembro.
Colocando de lado este ajustamento menor, o único ajustamento importante diria respeito aos anos julianos bissextos. Este era geralmente tornado "transparente" em termos de cálculo, acrescentando um 30º dia na lunação que terminava em fevereiro (um "bissexto" lunar). Todavia, na presença do bissexto solar, e porque a lunação já havia terminado antes do dia 24 de fevereiro (o sítio do bissexto), tornava-se necessário interpretar e convencionar o dia assinalado pelo Áureo Número sequente como sendo o último dia e não o 1º da lunação (mês lunar) seguinte.

As datas relevantes (início das lunações intercaladas), associadas aos anos do ciclo em que se verificam, estão assinaladas com asterisco na coluna "AN". Vamos verificar a "mecânica" das intercalações, relacionadas com o "acumular" dos dias da epacta.
Explicação claríssima (aqui trad. e abrev.) do racional que subjaz pode ser encontrada no Compendio Metodico Y Claro Del Cómputo Eclesiástico Antiguo Y Moderno, de Don Pedro Del Rio (Madrid, Imprenta Real, 1790), pag. 61:
"Assim, juntando as "epactas lunares" (o excesso do ano solar relativamente ao lunar) dos três primeiros anos do ciclo, chegamos a 33 dias intercalares. Por isto se intercala 1 mês no 3º ano lunar, sobejando 3 dias de epacta. Os 3 anos seguintes acumulam mais 33 dias que, acrescidos dos 3 que sobraram, totalizam 36 (logo, um novo mês é intercalado neste 6º ano). Pela mesma razão, no final do 9º ano acumulam-se mais 33 dias, acrescidos dos 6 residuais referidos totalizam 39. Intercalado outro mês, sobejam 9 dias. Os anos décimo e undécimo acumulam por si mesmos 22 de epacta, acrescidos dos 9 dias referidos, totalizam 31 dias. Assim, o ano 11º inclui outro mês embolísmico, sobrando desta vez somente 1 dia. Agregado ao triénio que se segue chega-se a um total de 34 dias. Deste modo, o ano 14º do ciclo inclui mês embolísmico, sobrando doravante 4 dias de epacta. No ano 17º do ciclo juntam-se novamente 33 dias, acrescidos dos 4 residuais, totalizando 37. Novo mês embolísmico e sobram, desta vez, 7 dias. Os últimos dois anos do ciclo acumulam 22 dias de epacta que, com os 7 que sobraram, totalizam 29 dias. Por isto mesmo, o último ano do ciclo (19º) inclui um mês embolísmico que não é completo como os demais (i.e., possui somente 29 dias)."

Na literatura medieval é necessário acautelar as referências ao nº de ordem do ano em causa no ciclo decemnovennalis. Isto deve-se ao facto de o ciclo alexandrino começar em setembro, enquanto aquele referido por alguns autores latinos como "nosso" começar em janeiro. Esta "duplicidade" surge, explicada, no excerto de Grosseteste que disponibilizamos infra.
Historicamente, o cômputo alexandrino evoluiu da utilização do ciclo de 8 (oktaeteris) para o de 19 anos, onde podiam ser integrados 228,5 meses lunares de 29 dias, mais 7 intercalares de 30 dias cada, acrescendo ainda 4 dias relacionados com os anos bissextos. Porque sobejava 1 dia após esta soma, impunha-se o chamado saltus lunae, omitindo 1 dia no final do ciclo.
Vejamos
a sequência dos anos comuns (C) e embolísmicos (E), respeitando a
divisão, pouco relevante para o cálculo mas mantida por conveniência,
entre ogdoas e hendecas (intervalos de 8 e 11 anos, respetivamente): CCECCECE / CCECCECCECE (Wallis, 1999: xlvi). A seguinte tabela das intercalações respeita o calendário alexandrino, com início em setembro:
| ano III | 2 dez. |
| ano VI | 2 set. |
| ano VIII | 6 mar. |
| ano XI | 4 dez. |
| ano XIV | 2 nov. |
| ano XVII | 2 ago. |
| ano XIX | 5 mar. |
Estrutura do Ciclo Alexandrino de 19 Anos
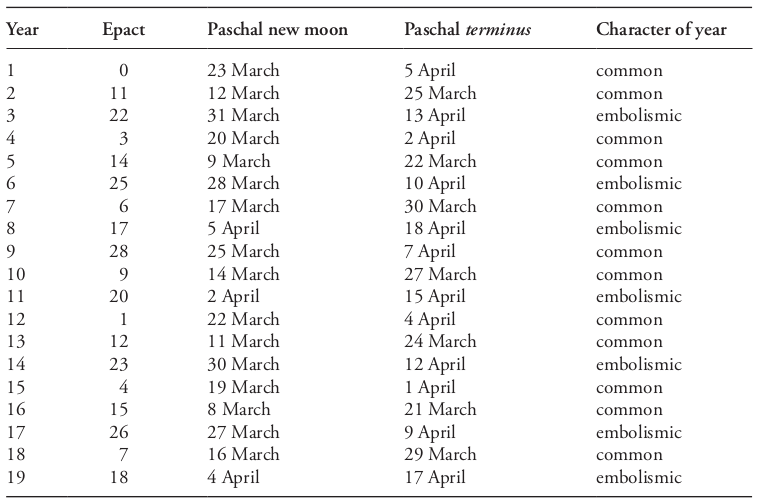
(Nothaft, Philipp, Scandalous Error - Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford/New York, Oxford University Press, 2018: Table 2.1, p.47; o "Término Pascal" é, na prática, a data do plenilúnio Pascal)
Grosseteste,
mais tarde, elenca a seguinte sequência padronizada (adotando um
referencial "juliano") de intercalações ou lunações extraordinárias
inseridas (ano do ciclo entre parêntesis):
| 1ª (II) | 2 dez. - 31 dez. |
| 2ª (V) | 2 set. - 1 out. |
| 3ª (VIII) | 6 mar. - 4 abr. |
| 4ª (XI) | 3 jan - 1 fev. |
| 5ª (XIII) | 2 nov.- 1 dez. |
| 6ª (XVII) | 2 ago. - 31 ago. |
| 7ª (XIX) | 5 mar. - 3 abr. |
Seguidamente a colocação das sete lunacões embolísmicas no calendário lunar, seguindo o texto do Compotus correctorius do referido autor Inglês, circa 1220. Utilizada versão inglesa vertida do latim por Philipp Nothaft, The Ordered Project Universe:
A 1ª lunação das 7 do "ciclo das epactas" (não confundir com o posterior e não relacionado cyclus epactarum gregoriano) começa no dia 2 de dezembro (o nº 2 significando o novilúnio) e termina no último dia de dezembro. Pertence ao 3º ano do referido ciclo das epactas (que começa sempre mais cedo, em setembro, i.e., calendário alexandrino; refira-se que aqui "epactas" é somente outra maneira de referir o ciclo de 19 anos, estas correspondendo reciprocamente aos anos deste; a relação é óbvia: tal como o embolismo ou intercalação, a epacta deriva do mesmo excesso de 11 dias). Pertence todavia ao ano II do ciclo de 19 (estabelecendo como referência o mês de janeiro sequente). Neste ano do ciclo há sempre duas lunações de 30 dias (completas) consecutivas, a embolísmica e a de janeiro. Sendo bissexto, acrescem as de fevereiro (devido ao dia extra) e a de março.
(N.B.: o autor utiliza "ciclo das epactas" como sinónimo do ciclo de 19 anos alexandrino, pelo qual a epacta é regulada; de facto, as epactas traduzem o devir deste ciclo através do excesso acumulável de dias do ano solar sobre o lunar)
A 2ª lunação embolísmica começa no dia 2 de setembro e termina no dia 1 de outubro. O nº 5 significa o novilúnio, pertence ao 6º ano do "ciclo das epactas" e ao ano V do ciclo decemnovennalis. Aqui há duas lunações completas consecutivas, a de setembro e a referida embolísmica.
A 3ª lunação embolísmica começa no dia 6 de março e termina no dia 4 de abril. O nº 8 significa o novilúnio, pertence ao VIII ano do ciclo decemnovennalis (o mesmo para o outro ciclo). Neste ano do ciclo de 19 há duas lunações seguidas de 30 dias (completas), a de março e a embolísmica. Se o ano for bissexto serão quatro consecutivas (contando com as anteriores de janeiro e fevereiro). Neste ano do ciclo, o desenvolvimento das lunações cria uma falha na determinação da "idade" da Lua através da utilização da epacta (17) e do regular (11 para maio) no início de maio e julho. A regra falhava e dava um resultado aumentado em 1 dia. Daqui o verso Fallitur octavo cum Mayo Julius anno (maio e julho falha no ano oitavo, do ciclo).
A 4ª lunação embolísmica começa no dia 3 de janeiro e termina no dia 1 de fevereiro. O nº 11 significa o novilúnio, pertence ao XI ano do ciclo decemnovennalis (o mesmo para o outro ciclo). Neste ano do ciclo de 19 há duas lunações seguidas de 30 dias (completas), a de janeiro e a embolísmica. Se o ano for bissexto serão quatro consecutivas (contando com as sequentes de fevereiro e março). Neste ano do ciclo, o desenvolvimento das lunações cria uma falha na determinação da "idade" da Lua através da utilização da epacta (20) e do regular (9 para março). A Lua devia ter 29 dias de “idade” pela regra mas apresenta 28 na realidade. Sendo bissexto, a compensação estava feita: Ni sit bissextus fallit Martem endeca primus (o primeiro (ano) da hendecas (intervalo de 11 anos) engana março, exceto se bissexto). Todavia, o dia extra do bissexto criava um novo erro caso a lunação de março começasse antes da intercalação do dia bissexto, acautelada pelos computistas.
A 5ª lunação embolísmica começa no dia 2 de novembro e termina no dia 1 de dezembro. O nº 13 significa o novilúnio, pertence ao XIII ano do ciclo decemnovennalis (e ao 14º do ciclo das epactas). Neste ano do ciclo de 19 há duas lunações seguidas de 30 dias (completas), a de novembro e a embolísmica. Pelo facto de serem ambas completas foi necessário colocar o 13 na tabela associado ao dia 2 de novembro, junto do 2, que já estava no dia 3 desse mês. Se o 13 fosse colocado no dia 1, a lunação acabaria demasiado cedo.
A 6ª lunação embolísmica começa no dia 2 de agosto e termina no dia 30 de agosto. O nº 16 significa o novilúnio, pertence ao ano XVI do ciclo decemnovennalis (o mesmo para o outro ciclo). Esta lunação vai buscar o excesso de 11 dias do ano XVII do ciclo, (setembro é a origem do ciclo das epactas). Apesar de estar colocada antes deste, pode ser considerada no dito XVI pois o final desta lunação acontece no início do XVII ano. Tanto a lunação embolísmica como a de setembro são completas.
A 7ª lunação embolísmica começa no dia 5 de março e termina no dia 3 de abril. O nº 19 significa o novilúnio, pertence ao ano XIX do ciclo decemnovennalis (o mesmo para o outro ciclo). Neste ano do ciclo há sempre duas lunações de 30 dias (completas) consecutivas, a de março e a embolísmica. Sendo bissexto acrescem as precedentes de janeiro e fevereiro. Neste ano do ciclo, o desenvolvimento das lunações cria uma falha na determinação da "idade" da Lua através da utilização da epacta (18) e do regular (9 para março, 11 na tradução, obviamente um lapso). Também aqui o cômputo aumenta erroneamente um dia à "idade" atual da Lua.

NB: a Reforma do Calendário trouxe ajustamentos às incorreções da repetição do ciclo metónico articulado com o calendário "antigo" e ao desfasamento verificado entre o plenilúnio convencional e o astronómico (mais de 3 dias em cada milénio). Aqui, os anos embolísmicos são os seguintes: 3º, 6º, 9º, 11º, 14º, 17º e 19º (De Saint-Allais, M., L'art de vérifier les dates des faits historiques, des chartes..., Tome premier. Valade, Imprimeur du Roi, Paris, 1818, p.67).