Astronomia - apontamento histórico

Detalhe de tapeçaria Flamenga, provavelmente de Tournai (Doornik), c.1500-1515, (Röhsska Museet, Göteborg). O astrónomo segura uma esfera armilar e, à sua direita, a Musa da Astronomia aponta para o céu.

N.B.: Esta página, como referido em epígrafe, colige alguns tópicos fundamentais, não uma sequência cronológica rígida de desenvolvimentos.

"...Haja luminares no firmamento do céu para separar o dia da noite. Sirvam eles de sinais para marcar estações, dias e anos." (Gn. 1,14)

"...But back when the sky was not just an illusion in blue but a sphere of activity, people noticed the more obvious things and, like ourselves, fashioned an understanding of the cosmos from them." (Krupp, E. C. (ed.), In Search of Ancient Astronomies, Chatto & Windus, 1977)

"A partir do raciocínio e do desígnio de um deus em relação à geração do tempo, para que ele fosse engendrado, gerou o Sol, a Lua e cinco astros, que têm o nome “planetas”, para definirem e guardarem os números do tempo." (Platão, Tim., 38c; Rudolfo Lopes [trad.], Centro de Estudos Clássicos e Humanísticos, Universidade de Coimbra, 2011)

Segundo o Thesaurus Linguae Grecae (TLG, University of California), a mais antiga referência à palavra "Astronomia" acontece na comédia "As Nuvens" (Νεφέλαι, Nephelai), de Aristófanes, c. 420 a.C. Décadas depois ἀστρολογία ("astrologia") surge em textos de Isócrates e Xenofonte. Em Roma, é na tragédia Iphigenia de Quintus Ennius, que viveu durante a República, que encontramos (fr. 185–7; ed. H. D. Jocelyn, Cambridge University Press, 1967) a primeira utilização do termo astrologi em Latim, referindo as suas profecias baseadas no nascimento das constelações.

Pormenor de estela em basalto do rei Marduk-Apla-Iddina (Babilónia, séc. XII a.C.). Neste kudurru (i.e. estela de registo, marco de limitação), a deusa Gula/Ninkarrak (Medicina) surge acompanhada pelo Escorpião, pelo crescente lunar de Sin, pela estrela de Ishtar (Vénus) e por Shamash, o Sol.

To the ancients, the sky was a source of power that drove the seasons and ordered the world. (Krupp, E.C. (2015). Astronomy and Power. in: Ruggles, C. (ed.) Handbook of Archaeoastronomy and Ethnoastronomy. Springer)

Os símbolos cosmológicos e celestes proporcionam instantaneamente, até de modo inconsciente, o reconhecimento das estruturas que a nossa psique "impõe" à envolvente. Cosmos (por oposição a Caos) significa "o Todo Ordenado" e, neste sentido, o próprio conceito reflecte os padrões e princípios da interpretação que fazemos dos acontecimentos que experenciamos. Tempo e Espaço formam a tessitura da ordem natural. Padrão, ciclo e ordem. A própria Ciência (no sentido clássico de scientia) começa justamente no reconhecimento de padrões. Os "universos" que concebemos reflectem as nossas percepções da ordem. Tal como os nossos antepassados, continuamos a pensar simbolicamente. Dependemos dos símbolos para comunicar, tanto o vulgar como o sublime. E apesar da linguagem do nosso sistema de crença (doravante 'secularizado') se ter alterado, continuamos a lidar com o céu. (vide Krupp, E. C., Echoes of the Ancient Skies, Oxford University Press, 1994 (1983), pp. 312-15)

Baseando-se no estudo dos espaços pessoais culturalmente definidos, sua escala, percepção e influência na interacção comportamental (Proxémica), desenvolvida pelo antropólogo Edward T. Hall nos anos 60 do século passado, o autor C. E. Roth (The Sky Observers Handbook, Prentice Hall Press, 1986, p.4 et seq.) salientou como a consciência do céu (entendido na sua plenitude metereológica e astronómica) tem decrescido no confinamento das sociedades contemporâneas. A gigantesca abóbada revela a nossa diminuta escala e limites (i.e. coloca-nos em perspectiva), por isso muitos preferem habituar-se à sua presença, não deixar a sua percepção interferir ou os seus fenómenos entrarem na consciência regularmente. Segundo Anthony Aveni, vivemos e trabalhamos em "clausura", em compartimentos, geralmente através de mediação tecnológica digital e afastados da natureza. O céu tornou-se quase irrelevante, excepto pelos detalhes meteorológicos quotidianos (e.g., se chove ou faz sol). Pelo contrário, o universo dos nossos ancestrais era "participatório": [...] for most of human history, the sky was relevant. People paid attention to the rising and setting sun, the phases of the moon, the coming and going of each of the planets. The relative perfection of the firmament beckoned for human connection. The first crocus might arrive a bit late, the last snowfall a little early, but I know that when Arcturus, the brightest star in the northern hemisphere, makes its first annual appearance in the east after sunset, it’s my birthday. The sky became the logical medium to mirror the ordered lives our species strove to lead. For ages it would serve as the storyboard for morally based tales of heroism and adventure. From season to season people found meaning in the dance of the cosmic denizens who resided in the world above. (In the Shadow of the Moon, Yale University Press, 2017, pp.4-5).

Osso do Paleolítico com prováveis marcações posicionais relacionadas com a contagem do tempo recorrendo à Lua (abrigo rochoso de Blanchard des Roches, França; fotografia: Michael Rappengluck)

A contemplação do céu conduziu à verificação da existência de fenómenos que, repetindo-se com suficiente regularidade, permitiram estabelecer padrões ou ciclos naturais de tempo: sucessão dos dias e das noites, fases da Lua, estações do ano, etc. Os fenómenos atmosféricos e meteorológicos mereciam igual escrutínio, integrando o grande "desafio". É plausível imaginar como os nossos antepassados adquiriram o conhecimento de alguns ciclos fundamentais para a interpretação da realidade envolvente e dos seus ritmos.

Um período astronómico de um astro é o tempo que este demora a percorrer um círculo que descreve. Quando o período diz respeito a vários astros, trata-se do período dos seus movimentos combinados, partindo de um determinado ponto ou aspecto (configuração), até que retornam ao mesmo ponto ou configuração, compreendendo exactamente um número de revoluções completas de cada um dos intervenientes.

O historiador das ciências exactas Asger Aaboe definiu dois "níveis" de astronomia pré-científica. Ao menos evoluído associou, por exemplo, o nomear das estrelas e constelações mais proeminentes, a distinção entre estrelas fixas e planetas, a constatação de que a estrela da manhã e a estrela da tarde eram o mesmo objecto celeste (i.e. Vénus), o entendimento de que qualquer estrela 'fixa' não circumpolar nasce e se põe sempre nos mesmos pontos do horizonte, o que não acontece com os planetas nem com os luminares, ou a descoberta de que o primeiro aparecimento de uma estrela depois do seu intervalo de invisibilidade (nascimento helíaco) acontece sempre na mesma época do ano e pode portanto ser usado como indicador sazonal. Quanto à modalidade mais avançada, Aaboe também menciona alguns exemplos: a descoberta do ciclo "metónico" que faz equivaler 19 anos [tropicais] com 235 meses lunares sinódicos, uma excelente base para o calendário, supostamente introduzido por Méton em Atenas e que também encontramos na Babilónia e na China; o ciclo de 8 anos do planeta Vénus, durante o qual este percorre o seu curso sinódico cinco vezes, isto é, surge como estrela da manhã cinco vezes, como estrela da tarde cinco vezes, torna-se retrógrado outras cinco e assim por diante, voltando no final praticamente à mesma posição em relação às estrelas e ao Sol. O ciclo encontra-se com ligeiras modificações (bem como ciclos mais sofisticados para os outros planetas) até ao final da literatura cuneiforme, também foi conhecido na China e foi muito importante na cultura Maia; por fim, os chamados ciclos de eclipse, que apesar de rudimentares podiam ser utilizados para antecipar "avisos de eclipse", isto é, reconhecer as sizígias nas quais podia eventualmente acontecer um eclipse solar ou um eclipse lunar. (A. Aaboe,"Scientific Astronomy in Antiquity", in: F. R. Hodson (ed.), The Place of Astronomy in the Ancient World, Published for The British Academy by Oxford University Press, 1974, pp.21-22).

E o que era 'astronomia científica' segundo A. Aaboe?
"I do not wish to call an astronomical theory scientific until it gives us control over the irregularities within each period and thus frees us from constant consultation of observational records." (Op. cit., p.23). E adiante: "Since Ptolemy’s Almagest we have wanted our planetary theories to enable us to answer the question: given the time, where is the planet? Thus we consider time the independent variable and seek means of deriving all other information from it." (ibid., p.32)

A abordagem arqueoastronómica (hoje habitualmente designada Cultural Astronomy) permite inferir a apreensão de ciclos fundamentais, ainda na Pré-História. Em primeiro lugar, o movimento diurno do Sol, a alternância do dia e da noite, o Dia. A observação do Sol, em dias sucessivos, relativamente ao horizonte e a modificação da trajectória do astro, com afastamentos para norte e para sul, determinando os solstícios (pontos extremos do trajecto) e os equinócios (pontos intermédios do trajecto, dias nos quais a duração dos períodos de luz e de obscuridade são exactamente equivalentes). Daqui se infere, no retorno a um momento específico deste ciclo, uma duração determinada: 365 dias, o Ano. Do mesmo modo se percebe a concatenação das estações deste ciclo, com as profundas alterações na natureza, no clima. A relacionação dos ciclos do Sol e da Lua deve ter sido uma das prioridades para os nossos antepassados distantes, bem como o conhecimento da dinâmica do céu nas diversas épocas do ano. E este conhecimento foi transmitido de geração em geração, permanecendo na tradição popular das diversas culturas e relacionando-se com os rituais, as actividades agrárias e o calendário. [N.B.: os calendários eram, e são, uma maneira complicada e muitas vezes "desajeitada" de acomodar certos ritmos naturais que não incluem um número exacto de dias no mês lunar ou no ano solar, nem um número exacto de meses num ano.]

"A common place where stars were given simple names and, most importantly, showed the way to pilgrims, marked the time of night, or set the rhythms to sow seeds or harvest crops and fruits." (Piero Barale, Lost Skies of Italian Folk Astronomy, in Ruggles, (ed.), "Handbook of Archaeoastronomy and Ethnoastronomy", Springer, 2015, p.1756).

Tudo terá provavelmente começado com o desenvolvimento de métodos que lidavam com determinados fenómenos astronómicos segundo um sistema de coordenadas baseado no horizonte do observador. Quanto o Sol é observado sistematicamente, percebe-se que não "nasce" nem se "põe" exactamente nos mesmos pontos do horizonte todos os dias, mas que (no hemisfério norte) o seu orto (nascimento) e o seu ocaso oscilam entre dois limites norte e sul em relação ao ponto leste geográfico e o mesmo em relação ao ponto oeste no que aos ocasos diz respeito. Somente em dois dias do ano se verifica que nasce e se põe exactamente nas direcções leste e oeste, respectivamente. São os equinócios. A dinâmica descrita determina a variação do tamanho dos dias e das noites que experimentamos ao longo das estações do ano. A duração do ano em dias podia ser aferida medindo o intervalo que o sol demorava sucessivamente a chegar a um dos pontos extremos (os solstícios), deslocado mais para norte ou para sul no horizonte (no nascimento e no poente), o que acontece no início do Verão e no do Inverno). Em rigor, podia sê-lo utilizando qualquer outro ponto fixo de referência no horizonte.

A investigação astronómica começou por basear-se, decerto, no Horizonte e nos fenómenos astronómicos em relação a "marcadores" reconhecíveis nessa linha paisagística onde os tempos das estações do ano e as direcções do espaço podiam ser intercambiáveis nas suas designações. Em algumas regiões é comum encontrar alinhamentos megalíticos colocados em função de um ponto no horizonte que, na época em foram erguidos, estaria relacionado com o nascimento ou do ocaso do Sol nos solstícios ou nos equinócios (Roy, Jean-René, L'Astronomie et son Histoire, Presses de l'Université du Québec/Masson, 1982)

Os pontos cardeais determinavam-se a partir do movimento dos astros na abóbada celeste. As estrelas mantinham as suas posições relativas e algumas eram circumpolares, nunca se escondendo sob o horizonte. Unindo os pontos luminosos, formaram-se padrões facilmente reconhecíveis. Na mesma época do ano, podiam observar-se as mesmas estrelas e asterismos. Não se conhecia a sua natureza. Tão tarde quanto o século XIII, ainda lemos no "Libro del Saber de Astrología" de Alfonso X (a que o editor Rico y Sinobas chamou, sem qualquer respaldo nos manuscritos, "Libros del saber de Astronomía...", vide Laura Fernández Fernández, Arte y ciencia en el scriptorium de Alfonso X el Sabio, 2013, p.214), que não tinham luz própria, recebiam-na do Sol:

"Ca las estrellas non son en sí. sinon querpos redondos, et fuertes, et llanos, et apareíados para rescebir luz del sol. assí cuemo la el sol rescibe de Dios." (M. Rico y Sinobas (ed.), Madrid, 1863; Tomo I, p.16)

O Sol tinha, em relação às estrelas, um movimento inclinado quando comparado com a direcção do seu movimento diurno (devido, como sabemos, à inclinação da eclíptica). Movimentos análogos terão sido compreendidos relativamente ao outro luminar. A Lua nascia e descia em pontos diferentes do horizonte, alterando a sua posição para norte ou para sul, e atravessava diversas fases, num ciclo que se repetia em aproximadamente 28 dias: o Mês. No nascimento e no ocaso, o valor do afastamento angular máximo (norte ou sul) assumia um ciclo de cerca de 18 anos e meio (vide Alarsa, Flávio, Faria, Romildo P., et al., Fundamentos de Astronomia, Papirus, 1982, 1º cap.). Os pontos do horizonte eram a referência para o nascimento e ocaso dos principais corpos celestes ("marcadores") e, provavelmente, pelo menos desde o Neolítico, as direcções coincidiam com as designações usadas para as estações do ano e momentos dos equinócios e solstícios. Podemos especular e inferir que os nossos antepassados remotos conheciam a sua paisagem e provavelmente nomeavam as direcções como, por exemplo, a "do Verão" ou talvez "das chuvas". Do mesmo modo, mais tarde, os antigos navegadores, nos seus rumos, recorriam a uma orientação que fazia equivaler os abstractos pontos geográficos aos ventos (i.e. os ventos eram as direcções), por exemplo (no Mediterrâneo): Tramontana, Levante, Ponente, Maestro, Libeccio, Ostro, etc. Em Português ainda chamamos "rosa-dos-ventos" à representação esquemática das direcções geográficas.

Arqueoastronomia (hoje mais conhecida como "Astronomia Cultural") é a área multidisciplinar que estuda a intencionalidade simbólica e cultural da interpretação dos fenómenos astronómicos pelos povos pré-históricos, por exemplo na construção dos seus monumentos ou na organização dos seus ciclos de contagem do tempo. Como precursores apontam-se os esforços de William Stukeley, John Aubrey, Henry Chauncy, Richard Proctor, Charles Piazzi Smyth ou Norman Lockyer. De modo mais consolidado, Alexander Thom (1894-1985) foi uma figura pivotal entre os anos 30 e 70 do séc. XX, abrindo perpectivas para as investigações actuais de Anthony Aveni. Clive Ruggles ou E. C. Krupp. Dos equívocos e especulações aos progressos conseguidos nesta área, permanece a dificuldade em estabelecer quais as orientações astronómicas previstas pelos seus antigos construtores e (supostos) intérpretes do céu. Ademais, como Jean-René Roy explica, devido à Precessão do eixo de rotação da Terra ao longo de um período de cerca de 26000 anos, o alinhamento por puro acaso de um megálito com uma das 45 estrelas mais brilhantes, em qualquer século, é de da ordem dos 10%. Por essa razão, um qualquer alinhamento relevante é "inevitável" num período de 1000 anos. É, portanto, crucial, determinar a idade dos monumentos, pelo menos com a aproximação de alguns séculos. (L'Astronomie et son Histoire, Presses de l'Université du Québec/Masson, 1982, p.76).

Sempre que se refere a Arqueoastronomia é quase obrigatório referir Stonehenge, pelo longo percurso de investigações (e muitas especulações sem fundamento!). Aqui, um registo dos azimutes de nascimento e ocaso do Sol ao longo do ano, bem como a variação mensal dos nascimentos e ocasos da Lua ao longo do período de 18,6 anos ("ciclo metónico") que os nodos lunares demoram a percorrer o círculo da Eclíptica. Elaborado para a latitude do site em causa. (Mills, H. Robert, Practical Astronomy: A User-friendly Handbook for Skywatchers, Albion Publishing, 1994, Fig. 2.17.5.). Este tipo de esquema, com orientação cardeal, é também um exercício pedagógico interessante para qualquer "observatório" amador.

O "mound" funerário de Newgrange (c.3200 a.C.), Irlanda. Durante algumas manhãs, em pleno Inverno, o Sol ilumina a tumba central ao fundo do longo corredor da entrada (Couper, H. & Henbest, N., The History of Astronomy, Firefly Books, 2007)

Os astrónomos da Meso-América observavam as posições dos astros que consideravam mais importantes visando através de dois paus cruzados em "X" para apontar as suas posições relativamente ao horizonte. Na ilustração: os Hopi-Navajo, da América do Norte, reconheciam os dias mais significativos do ano memorizando as posições do Sol relativamente a acidentes naturais proeminentes no seu horizonte, na paisagem que habitavam (Aveni, A., Old and New World Naked-Eye Astronomy, in: Brecher, K. and Feirtag, M. (eds), "Astronomy of the Ancients", The MIT Press, 1980, p.64)

"Astrólogo" nativo dos Andes: "ASTRÓLOGO, PVETA Q[VE] SAVE del r[r]uedo del sol y de la luna y [e]clip[se] y de estrellas y cometas ora, domingo y mes y año y de los quatro uientos del mundo para senbrar la comida desde antigua.". Guaman Poma de Ayala, Nueva corónica y buen gobierno, ca.1615; Det KGL. Bibliotek, GKS 22232 4º; 883 [897]. Repare-se no quipu que segura com a mão esquerda. No Peru pré-hispânico, utilizava-se um sistema de cordas e nós para registar e transmitir informação. O quipu (do Quechua khipu que significa “nó”) era um artefacto têxtil constituído por cordas e nós. Apesar da simplicidade do material, o quipu foi a base de um complexo sistema andino de arquivo e transmissão de informação.

Algumas "estrelas", para além do Sol e da Lua, deslocavam-se relativamente às demais. Os gregos distinguiram ambas as "categorias": aplane (lit. "que não se movem", sc. as chamadas "estrelas fixas") e planõmena / planètai (“que vagueiam”, sc. os planetas). Mais tarde é comum encontrar nos tratados em Latim um qualquer planeta designado como sidus errans, stella errans, etc. Os planetas moviam-se sempre numa faixa inclinada povoada de constelações em que predominavam representações de animais (Gr. zōidiakòs kýklos). Moviam-se quase sempre de oeste para leste (o que chamamos 'sentido directo'). Todavia, por vezes permaneciam praticamente estacionários (relativamente ao cenário de fundo proporcionado pelas estrelas fixas) por uma ou mais noites e invertiam o sentido do movimento (retrogradação), mais tarde retomando o sentido normal, directo (daí as chamadas "laçadas", que os nossos cosmógrafos do passado descreveram: as curvas 'desenhadas' pelos seus caprichosos movimentos).

"Their wandering course now high, now low, then hid,
Progressive, retrograde, or standing still,..."
(Milton, Paradise Lost. Book VIII)

N.B. Se as órbitas estivessem no plano da Eclíptica, não veríamos o "loop" ou curva a que chamamos 'laçada'. Para Ptolomeu (séc. II), e no contexto da solução geométrica geocêntrica entretanto ultimada, a explicação residia, justamente, na inclinação dos círculos que asseguravam as órbitas planetárias relativamente ao círculo a que chamamos Eclíptica.

Os planetas serão sempre objecto de curiosidade e fascínio. Outros fenómenos atmosféricos ou astronómicos (distinção irrelevante no passado) decerto fascinavam e pressagiavam, e.g., relâmpagos, meteoros, halos, cometas.

Na Mesopotâmia, a invenção da Escrita permitiu registar escrupulosamente as sistemáticas observações astronómicas, efectuadas ao longo de vários séculos por "ummanu", os peritos cujo ofício era estarem atentos aos augúrios na natureza (Whitfield, Astrology: A History, The British Library, 2001, p.9 et seq.). Ou seja, existia todo um "mecanismo burocrático" para observar e registar informação astronómica, preservando os registos resultantes.

Eis um excerto de um calendário estelar babilónico:

On the 1st of Nisannu [nome do mês] the Hired Man [asterismo que ocupava o lugar do nosso Aries] becomes visible [i.e. dá-se o seu "nascimento heliacal", primeira visibilidade imediatamente antes do nascimento do Sol].
On the 20th of Nisannu the Crook becomes visible.
On the 1st of Ajjaru the Stars [Plêiades] become visible.
On the 20th of Ajjaru the Jaw of the Bull becomes visible .
On the 10th of Simanu the True Shepard of Anu and the Great Twins become visible.

(MUL.APIN, tablet I, col. i, lines 1-5; Hunger, H, & Pingree, D. (trans.), MUL.APIN.: An Astronomical Compendium in Cuneiform. Archiv fur Orientforschung, Beiheft 24, Ferdinand Berger, 1989, pp. 40-41)

Um calendário estelar (Gr. parapegma) elencava e relacionava fenómenos astronómicos. Por exemplo, ortos e ocasos simultâneos das constelações ou asterismos, intervalo de dias entre visibilidades, etc. Permitia conhecer a época do ano e acautelar as tarefas agrícolas, económicas, religiosas... estruturando e organizando a vida da sociedade.

O arquivo incontornável, em todos os aspectos (dele faz parte, por exemplo, a Epopeia de Gilgamesh) é a biblioteca de milhares de placas em argila contendo textos em escrita cuneiforme associada ao rei assírio Assurbanípal (profundamente interessado na antiga cultura literária da Mesopotâmia, m. 631 a.C.), que coligiu ou mandou copiar os registos dos templos Babilónicos. O acervo (e outros ancilares) foi encontrado no sítio da antiga Ninive em meados do séc. XIX por Austen Henry Layard e Hormuzd Rassam. Processado de modo apressado e algo desorganizado, acumula material de diversas proveniências desse site arqueológico. Encontra-se, na quase totalidade, no Museu Britânico.

A utilização de um sistema sexagesimal, bastante acessível (facilmente divisível) para cálculos com fracções, poderá ter tido origem na estimativa do número de dias de um ano. Foi utilizado pelos povos da antiga Mesopotâmia desde o tempo dos sumérios. O seu uso prevalecente era científico (matemático), existindo concomitantemente outros sistemas noutras áreas de actividade. Recorria-se ao sexagesimal na divisão do tempo, bem como, antes de mais, na divisão da circunferência. Como se utilizava um sistema numérico sexagesimal, o percurso a observar foi dividido em 360º, bem como cada grau ("us") em 60 minutos. O dia foi dividido em 12 horas diurnas e 12 nocturnas, John Steele explica que a preocupação primária da astronomia na Mesopotâmia era a ocorrência de fenómenos regulares protagonizados pela Lua e pelos planetas: a duração da visibilidade da Lua em dias específicos em torno do novilúnio e do plenilúnio, o movimento da Lua e dos planetas através de um repertório de estrelas fixas de referência hoje conhecidas [na literatura especializada] como "Normal Stars", eclipses lunares e solares, os fenómenos sinódicos dos planetas (primeira e última aparição), as suas estações [quando os planetas "param" e passam do movimento directo, na mesma direcção do Sol e da Lua, ao retrógrado, ou vice-versa] e os nascimentos acrónicos [quando um astro nasce vespertinamente, em oposição ao Sol]. (The Influence of Assyriology on the Study of Chinese Astronomy in the Late Nineteenth and Early Twentieth Centuries, in: Mak, Bill M. & Huttington, Eric (eds.), "Overlapping Cosmologies in Asia...", 2022, p.23; trad. e aditamentos entre parêntesis rectos são nossos).

O conhecimento do movimento da Lua era de extrema importância para a medição do tempo. O início do mês era originalmente determinado por observação concreta do fino crescente. Todavia, com a acumulação das observações, os babilónios, por volta de 400 a.C., estavam em condições de compreender que os os movimentos dos luminares não revelavam velocidade constante no seu percurso contra o "cenário" das estrelas. Conceberam representações aritméticas do movimento da Lua: ou assumindo um movimento lunar com velocidade fixa na primeira metade do seu ciclo e outra, também fixa mas diferente, na segunda metade; um método refinado que previa um incremento regular na velocidade entre um mínimo e um máximo na primeira metade, seguido de um decréscimo até um mínimo na segunda metade do ciclo.

As suas unidades de medição do comprimento/tempo correspondiam à rotação do céu em 1º e 30º (1 signo zodiacal). F. R. Stephenson (Historical Eclipses and Earth's Rotation, Cambridge University Press, 1997, p.118), resume o que julgamos conhecer dos métodos e medidas utilizados na Mesopotâmia: o US tinha uma duração fixa de 1/15 de hora (=4 minutos ou 1º). Dividia-se em 60 GAR (ou NINDA). US deveria traduzir-se como "grau-tempo", pois mede efectivamente uma duração, o tempo que o arco do céu demora, como sabemos, a rodar cerca de 1º. O beru continha 30 US, equivalendo portanto a duas horas. Na Grécia, que importará estas unidades, encontramos a designação chronoi isemerinoi ("tempos equatoriais"), mas o sistema grego repalda-se no recurso a horas (equinociais [iguais] ou, alternativamente, sazonais). Convém referir que os Babilónios utilizavam unidades diferentes para as medições angulares entre dois corpos celestes: o "cúbito", KUS (equivalendo a cerca de 2º ou 2.5º), dividido em 24 "dedos" (SI).

Historicamente, a divisão mais natural do dia ou da noite terá sido em 2, 3 (usada na Babilónia) ou 4 intervalos iguais (no Egipto). O. Neugebauer sugeriu uma curiosa explicação para o método desenvolvido na Mesopotâmia: sabemos que desde a época Suméria existia uma medida de distância (danna), uma espécie de "milha" utilizada para medição de distâncias mais longas, gradualmente associada ao período de tempo que demoraria a percorrê-la. Esta medida, enquanto intervalo de tempo, foi "transferida" pelos babilónios para os intervalos no céu. Como havia sido subdividida em 30 US ou uS ou ush (i.e. "comprimentos", segundo O. N.), a amplitude do céu acabou dividida em 12 (12x30 = 360 partes). Aqui radicará a origem dos nossos "graus" e o procedimento astronómico de divisão do tempo em graus. (Some Fundamental Concepts in Ancient Astronomy (1941) "Studies in the History of Science", Univ. of Pennsylvania). Os povos da Mesopotâmia não possuiam o conceito de "esfera celeste" (vide Rochberg, F., The Heavenly Writing:..., 2004, Cambridge University Press, pp.126-7). As unidades de comprimento mais antigas foram os "dedos" (Gr. daktylos) e os "cúbitos".

O legado babilónico é incontornável. Clemency Montelle (Chasing Shadows: Mathematics, Astronomy, and the Early History of Eclipse Reckoning, The Johns Hopkins University Press, 2011, p.6) resume:

"Metrological conventions and the ways in which these practitioners sought to measure and quantify celestial phenomena became the basis of astronomical reckoning and recording. These included expressions for units of length and magnitude (such as fingers [0;5º], cubits [2º]), and time and arc (such as degrees [UŠ], the division of the circle into 360º, the lunar day or tithi—a thirtieth of a mean synodic month, the division of the hours of daylight into 12 [beru]). Calendrical conventions (such as division and arrangement of the year, intercalary conventions, parapegma) and chronological systems (such as the use of the Seleucid era) were assimilated. Tools such as the gnomon, the water clock, and the hemispherical sundial became essential accessories for astronomers. Babylonian parametersBabylonian parameters and period relations proved inspirational and fundamental for all subsequent efforts at more involved celestial models. Among them were the simple lunar period relation (nine anomalistic months equals 248 days), the later-named Metonic cycle (19 years equals 235 synodic months) and Saros cycle for eclipses (18 years ≈ 223 synodic months ≈ 242 draconitic months ≈ 239 anomalistic months), length of daylight ratios (notably 3:2 for Babylon), the length of the mean synodic month (29;31,50,8,20), lunar latitude (1 year = 12;22,8 synodic months), and so on. Techniques used to model celestial phenomena were adopted, including linear zigzag 'functions' and arithmetical sequences to model phenomena such as rising times.".

Traduzindo uma base sexagésimal que já era utilizada na Mesopotâmia e que influenciou astrónomos e geómetras ao longo dos séculos (nomeadamente na subdivisão do grau em 60 partes, que Ptolomeu implementou), a palavra "minuto" deriva do Latim medieval pars minuta prima, significando "a primeira parte pequena", adequadamente a sexagésima parte do grau e depois da hora. O cosmógrafo Manoel de Figueiredo escrevia no início do séc. XVII: "E este foi o numero de 60 porque nenhum ha ate 100 que se diuida em mais inteiros que elle." (Figueiredo, Chronographia Reportorio dos Tempos..., Lisboa, Jorge Rodriguez, 1603, fól. 43v). Tornou-se pertinente na contagem do tempo com o aperfeiçoamento dos relógios mecânicos. Todavia, o adjectivo minutum, “coisa minúscula”, foi previamente usado de várias maneiras para 1/15 hora (4 min.), 1/10 hora (6 min.) e 1/60 dia (24 min.); mas nunca indicou 1/60 hora, que era um ostentum (Holford-Strevens, The History of Time: A Very Short Introduction, Oxford University Press, 2005, p.9). Havia outras subdivisões: puncta (pontos), momenta (impulsos), etc. Na Idade Média tardia, no entanto, encontramos uma nova divisão sexagesimal da hora em primae, secundae e tertiae minutae (partes, entenda-se). Este sistema, já utilizado para divisões angulares, deu origem aos nossos 'minutos' e 'segundos'. A última (tertia, a terceira) passou a ter uma abordagem decimal.

Os sistemas mecânicos utilizados na vida monástica a partir do séc. X, que funcionavam usando água, eram descritos como relógios mas na realidade eram simples "alarmes": não marcavam a hora, antes estavam ligados a um mecanismo simples que após determinado intervalo fazia tocar uma sineta, avisando o monge incumbente para avisar a comunidade para as orações diárias. Os primeiros relógios mecânicos, que surgem nos séculos XIII e XIV, quando o tempo se começa a laicizar, eram extremamente imprecisos e só tinham o ponteiro das horas (Aron Gurevitch, As Categorias da Cultura Medieval, Lisboa, Caminho, 1991, p.175).

É pertinente referir que a astronomia na Mesopotâmia não se preocupava com as latitudes, somente com as longitudes, excepto no caso da Lua (servindo a determinação dos eclipses e do primeiro crescente lunar). Na abordagem grega, os planetas serão corpos em órbitas, a determinar geometricamente. Jo Marchant resume de modo algo "épico" a auspiciosa combinação das abordagens: "The Babylonian arithmetic progressions yielded precise predictions but included no three-dimensional structure, while the Greeks had geometric models but no accurate numbers. Neither approach on its own could produce a complete description of the sky. When they came together, the science of astronomy was born." (The Human Cosmos: Civilization and the Stars, Dutton, 2020, p.62). Entretanto, em 2016, o historiador Mathieu Ossendrijver da Universidade Humboldt de Berlim, argumentou que sacerdotes na Mespotâmia também já utilizavam técnicas geométricas em alguns cálculos astronómicos. (“Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph", Science 351 (2016): 482-84)

Os Egípcios, por seu lado, utilizavam um calendário civil, agrícola, para a gestão do seu quotidiano (possuiam em paralelo um calendário lunar para as celebrações religiosas). Ao contrário dos povos da Mesopotâmia, foram condicionados pelo carácter primitivo da sua aritmética e geometria, impedindo uma interpretação precisa dos movimentos astronómicos mais complexos e subtis.

Na Mesopotâmia o dia era dividido em 24 horas: a parte diurna em 10 e a noite em 12 (sobrando 2 horas crepusculares em ambas as transições). Gradualmente foi adoptado um sistema de divisão em 12+12 horas. É deles que nos chega o dia de 24 horas. Estas horas eram sazonais (desiguais, duração variável em função da estação do ano e da desigual duração dos dias e das noites; e.g., dividia-se a noite em 12 períodos iguais, obviamente diferentes consoante as estações, maiores no Inverno e mais pequenos no Verão, em função da latitude do lugar).

D. R. Dicks (Early Greek Astronomy to Aristotle, Cornell University Press, 1970, pp.166-67) considerou provável que (apesar do afirmado por Heródoto) a origem da divisão grega do dia e da noite em doze partes (ou horas) fosse uma influência do Egipto, onde se terá desenvolvido a partir da tradição do recurso aos decanos (v. infra) enquanto "calendários" siderais.

Para os gregos, "hèmera" designava (neste contexto) o intervalo diurno, do nascimento ao ocaso do Sol; "nux" era o intervalo nocturno, complementar. Somente na época helenística (e prioritariamente num contexto científico, astronómico) se passará a ponderar a utilização de horas equinociais, iguais (calculadas em função da duração da hora nos dias dos equinócios), como sugerido por Hiparco (Hipparkhos) de Rodes, o astrónomo que iniciou o modelo de investigação matemática dos céus, que será adoptada por Ptolomeu.

Hiparco verificou que as quatro Estações do Ano não tinham exactamente a mesma duração. Na sua teoria solar, preservada e adoptada por Ptolomeu, reconhece que se o Sol parece não ter um movimento uniforme, a Terra não poderá portanto estar exactamente no centro da sua órbita: deve ser "excêntrica". Ou seja, para gerar estas anomalias (intervalos irregulares), a Terra deveria ser deslocada, segundo os cálculos do astrónomo, 1/24 do raio do círculo percorrido pelo Sol e a linha entre a Terra e esse centro deveria fazer um ângulo de 65.2º com a direcção do Equinócio Vernal. Com estes parâmetros, o modelo respondia adequadamente aos fenómenos observados (v. esquema; fonte: The Cambridge Illustrated History of Astronomy, Cambridge University Press, p.41)

Todavia, verifica-se generalizadamente a utilização das horas sazonais até muito mais tarde, mesmo depois de surgirem os relógios mecânicos na Europa do séc. XIV (o desenvolvimento de relógios e outros equipamentos mecânicos acontece precisamente quando também assistimos à utilização de algoritmos mais complexos, nomeadamente astrológicos, num "crossover" tecnológico que incrementava o detalhe e a minúcia). Segundo L. Holford-Strevens (The History of Time: A Very Short Introduction, Oxford University Press, 2005, pp.8-9), os astrónomos gregos dividiam o dia natural em 24 horas equinociais ou iguais, cada qual com 15 moîrai ou ‘partes’ (a mesma designação que utilizavam para os graus da circunferência, pois em ambos os casos o total era 360; 1º equivale a 4 minutos de tempo). No contexto latino medieval, o adjectivo minutum, ‘coisa pequena’, foi utilizado de modo variável para 1/15 hora (4 min.), 1/10 hora (6 min.) e 1/60 dia (24 min.), mas nunca significou 1/60 hora, intervalo a que se chamava ostentum. Todavia, na Idade Média tardia encontramos uma nova divisão sexagésimal da hora em primae, secundae, e tertiae minutae (partes). Este sistema, já utilizado para as medidas angulares, deu origem aos nossos ‘minutos’ e ‘segundos’ Mas na contagem do tempo, a tradição e o sistema de base 12 dos mostradores dos relógios vão perpetuar a utilização de meias, quartos, etc.

Segundo Jo Marchant, a partir do desenvolvimento dos relógios mecânicos nasceu um "novo" tempo que nos dissociou dos ritmos da natureza: "powerful enough to weaken our bond with both God and the universe, and set the foundations of a new way of life." (The Human Cosmos: Civilization and the Stars, Dutton, 2020, p.96).

Calendário astronómico circular mesopotâmico. Este tipo de texto e de suporte, actualmente designado "Three Stars Each", é por vezes chamado, equivocamente, "astrolábio". Encontram-se exemplares a partir do primeiro milénio a.C. Grafavam as estrelas que, em cada mês, nasciam antes do orto do Sol. (Department of Western Asiatic Antiquities, The British Museum)

Paralelamente existia na Mesopotâmia uma antiga "geografia cósmica" de inspiração mitológica (os "caminhos" paralelos dos deuses Enlil, Anu e Ea). Entretanto, assiste-se à divisão do "caminho" (ou linha) percorrido por aqueles astros que deambulam (a Lua, o Sol e os planetas) em doze sectores iguais, de 30º cada. Existem evidências, na mesma região geográfica entre o Tigre eo Eufrates, de uma relação astrológica que atribui um dia a cada um dos sete planetas/deuses. Este intervalo de sete dias (semana) também coincide aproximadamente com a duração de uma fase lunar. O texto sagrado dos Hebreus referiu a Criação em sete dias (Gr. heptâmeron) e a semana de sete dias será mais tarde adoptada pelos romanos. Muitos idiomas modernos testemunham esta relação íntima entre os dias da semana e os planetas/deuses. A Astrologia helenística utilizará as chamadas "horas planetárias", que entrarão definitivamente nessa linguagem simbólica. Na época neo-babilónica já se conhece o que hoje designamos como saros, um período (223 meses lunares "sinódicos", ou seja, medidos pelas fases) que permitia determinar, aproximadamente, os eclipses da Lua e a probabilidade (mas não a geografia) dos solares. Criou-se um calendário lunar que exigia a utilização periódica de um décimo terceiro mês para o acertar com o ritmo das estações (pois estas respaldam-se no ano solar). Outro ciclo de dezanove anos relacionará as lunações com a recorrência de datas das fases no contexto do calendário solar, constituíndo referência dos calendários e do futuro computus eclesiástico [O ciclo de cerca de dezanove anos, idealizado segundo a tradição pelos gregos Meton e Euctémon mas com provável origem na Mesopotâmia, constitui um período aproximado que relaciona o mês e o ano (i.e., os ciclos aparentes da Lua e do Sol: é o chamado Ciclo Metónico, depois utilizado pelo nosso Calendário Litúrgico para a determinação das chamadas Festas Móveis. Este ciclo recorre a anos tropicais (i.e. sazonais), astronomicamente definidos. Aí se integram 235 meses lunares médios, que no final conciliam a mesma fase lunar com a mesma estação (momento relativo à estrutura de equinócios e solstícios), mas depende do calendário "local" caso também se pretenda a sincronização com a data, como acontece com a nossa Páscoa, que deve ser sempre a um domingo].

O calendário, pela sua importância, constituiu uma motivação mas constata-se que, por exemplo entre os gregos, os ciclos mais sofisticados e precisos eram expostos em textos científicos mas os calendários civis das diversas cidades-estado demoravam a adoptá-los, não eram articulados e estavam sujeitos a interpolações, geralmente pouco sistemáticas, ao sabor das iniciativas dos respectivos burocratas. Aristófanes, n'As Nuvens (Nephelai) faz a Lua queixar-se da falta de cuidado dos atenienses em combinar adequadamente os dias com as suas fases.

O reconhecimento de recorrências nos diversos períodos planetários foi determinante e recua aos antigos astrónomos da Mesopotâmia, que assim, pelo acúmulo de observações relevantes ao longo do tempo, conseguiram antecipar as posições da Lua e dos planetas e mais tarde gizar efemérides (da palavra grega para "diário"; hemera significa "dia"):

"The Babylonians had noticed the periodicity of the motions of the moon and the planets. For example, 71 years equals 65.01 synodic periods of Jupiter and 5.99 sidereal periods. Because these are very nearly whole numbers, the dates and longitudes of the interesting features of Jupiter’s motion (as listed above) in any one year will be repeated almost exactly 71 years later. Therefore the data for Jupiter this year can be foretold by looking at the data for 71 years ago. A compilation for a planet used for this purpose is called a 'goal-year text’ (a somewhat awkward literal translation of the German "Zieljahrtexte"). Another interval that works well for Jupiter is 83 years; 59 years serves for Saturn, 79 and 47 years for Mars, 8 years for Venus, 46 years for Mercury, and 18 years for the moon." (Thurston, Early Astronomy, Springer-Verlag, 1994, p.69)

Durante o período Babilónico tardio (c. 750 a.C - 75 A.D.), os astrónomos respaldaram-se nos extensos e sistemáticos registos observacionais, desenvolvendo diversas técnicas empíricas para prever as posições futuras dos corpos celestes. Há diversos tipos de textos astronómicos não matemáticos, classificados por Abraham Sachs como: 1) Astronomical Diaries, 2) Goal-Year Texts, 3) Normal Star Almanacs, 4) Almanacs e 5) Lunar or planetary texts (A. J. Sachs, 1948, A Classification of Babylonian Astronomical Tablets of the Seleucid Period. Journal of Cuneiform Studies 2, 27 1-90). Os registos provenientes do "Diário" para determinado ano permitiriam, utilizando a periodicidade conhecida dos movimentos dos planetas e da Lua, antecipar as posições no 'ano-alvo' desejado. Alguns planetas tinham dois períodos ou ciclos, para diferentes fenómenos.

Os academicamente designados "goal-year texts" incluiam excertos de registos de determinados anos concretos, tendo em consideração os referidos períodos, antecipando a repetição da posição do planeta numa observação futura específica. Recorria-se a um "ano-base" e ao conhecimento dos períodos planetários (um ciclo no qual o movimento de um planeta se repete aproximadamente), promovendo os ajustamentos convenientes para cada planeta (i.e. correcções específicas e regulares para um dia concreto ou, mais genericamente, uma correcção mensal representando a deslocação do planeta ao longo de um mês). Estes textos podem ser considerados uma antecipação dos almanaques:

Various planetary periods are referred to in many Late Babylonian astronomical texts. By collecting together these periods and analysing their effectiveness, it was found that, generally, the most effective of the planetary periods were those which were used in the production of a particular type of text known as a Goal-Year Text. The Goal-Year Texts contain excerpts of astronomical observational records, with the planetary records having been taken from particular observation years with these planetary periods in mind – such that each planet‘s motion will recur during the same, specific, future year. (...) An analysis of theoretically calculated dates of planetary events showed that, if the Goal-Year Texts were to be used as a source for making empirical predictions, particular corrections (specific to each planet) would need to be applied to the dates of the planetary records found in the Goal-Year Texts. These corrections take the form of regular corrections to the day of an event (a date correction), and more irregular corrections of ±1 month (a month shift). (Gray, J. M. K., A Study of Babylonian Goal-Year Planetary Astronomy, 2009).

Num texto da tipologia "goal-year" para determinado ano (solar), a informação contida sob cada uma das colunas para cada planeta remeteria para um ano anterior, dependendo do planeta em causa e do correspondente ciclo utilizado. Os babilónios perceberam as circunstâncias das oposições e das conjunções dos diferentes planetas e os ciclos (que constituem uma boa aproximação) foram gizados de acordo com os seus períodos sinódicos (i.e. a recorrência das suas posições relativamente ao Sol). Método, que já surgiu numa época tardia, baseava-se nas posições observadas ao longo de séculos e registadas nos "diaries" (designação introduzida por A. Sachs). Assim, para o ano em que escrevemos estas linhas (2025 A.D.), o texto incluiria informação de 1954 para Júpiter (período de 71 anos no qual o planeta se "repete"; também havia um período de 83 anos); para Vénus replicaria informação de 2017 (período de 8 anos); para Mercúrio a informação de 1979 (há 46 anos), para Saturno a de 1966 (há 59 anos) e para Marte o que se verificou há 47 anos (ou em alternativa há 79 anos). Aplicava-se depois uma correcção de alguns dias (v. tabela seguinte) ou de graus. No caso de Vénus, por exemplo, subtraiam-se 4 dias. Era possível, deste modo, construir efemérides. (Pannekoek, A., A History of Astronomy, New York: Interscience Publishers, 1961, pp.54-55; Aaboe, A., Scientific Astronomy in Antiquity, in: F. R. Hodson (ed.), The Place of Astronomy in the Ancient World, Op. cit., 1974, p.23; Anderson, J., Astronomy the Babylonian Way, Journal of the Royal Astronomical Society of Canada, Vol. 106, No. 3 [June 2012], 108-11; Noel Swerdlow estudou mais aprofundadamente este assunto, nomeadamente nas suas complexidades: The Babylonian Theory of the Planets, Princeton University Press, 1998, pp.44, 54, 59, 61-62).

Pannekoek - períodossinódicos babilónicos

Os períodos sinódicos dos planetas e as correcções a introduzir segundo os babilónios (Pannekoek, 1961, pp.54-55).

As tabelas serão, como se sabe, o utensílio privilegiado para plasmar, extrair e veicular informação astrométrica. Obviamente comuns também mais tarde, na Idade Média, tanto no contexto Latino como no Islâmico (Ár. taqwīm, i.e. tabela, no sentido lato, translit. em Lat. como tacuinum ou attacium). Na antiga técnica helenística com raízes babilónicas (v. Almagesto IX,3) conhecida na literatura especializada, como vimos, como "goal-years", baseada no uso de ciclos específicos para pada planeta, os almanaques eram perpétuos. Os ciclos continham um número inteiro de anos durante os quais um planeta cumpria um número inteiro de revoluções sinódicas e zodiacais. Ou seja, um determinado número de anos (Julianos no contexto Latino medieval) no qual o planeta completava um número inteiro de revoluções em longitude e em anomalia ("inequalidade"). Na tabela seguinte (dados do Almagesto), verificamos, pegando por exemplo no caso de Saturno, que o planeta em 59 anos completa 57 revoluções sinódicas (i.e. assume a mesma posição em relação ao Sol, tendo como ponto de referência o observador terrestre) e percorre 2 vezes o ciclo zodiacal (demora cerca de 30 anos a percorrer uma vez os 360º dessa faixa).

NB: Era desconhecido (e parece tê-lo sido na Antiguidade) qualquer ciclo "perpétuo" deste tipo adaptado aos movimentos da Lua. Somente no século XIV seria encontrada uma solução: "...the final solution which allowed the use of almanac cycles for the computation of lunar position was reached towards the middle of the fourteenth century: both Ibn ʿAzzūz al-Qusanṭīnī (c. 1340) and Jacob b. David Yomtov (= Bonjorn) of Perpignan (c. 1361), used a new lunar cycle of 31 Egyptian years, 9 days, 23 hours, 34 minutes and 11 seconds, equivalent to 383.5 synodic months (767 consecutive syzygies), which solved the problem and was later used in Zacut’s Almanach." (Julio Samsó, On Both Sides of the Strait of Gibraltar: Studies in the history of medieval astronomy in the Iberian Peninsula and the Maghrib, Brill, 2020, p.883)

Também eram, no contexto mesopotâmico, obviamente observadas as datas do chamado nascimento helíaco dos planetas (quando estes começam a estar visíveis antes do orto [nascimento] do Sol), bem como, evidentemente, os ciclos dos planetas no seu percurso zodiacal completo, cujos valores aproximados são, na ordem ptolomaica inversa: Saturno (30 anos), Júpiter (12 anos), Marte (2 anos), Sol (365 dias), Vénus (348 dias), Mercúrio (339 dias), Lua (29 dias).

Todavia, D. R. Dicks minimiza a influência astronómica Babilónica (mas não a matemática, aí concordando com Neugebauer) pois considera os seus pressupostos e objectivos completamente alheados da ulterior abordagem grega, nomeadamente na sua total negligência pela geometria esférica (com todas as consequências limitadoras), ausência de qualquer esquematização matemática, holística, explicativa dos fenómenos, ausência de corpus teórico documentado (somente obtemos resultados aritmeticamente calculados ou observados), predominância no registo dos fenómenos tendo como referência o horizonte, confinamento do interesse a um limitado tipo de fenómenos, etc.:

"The chief aim of the Babylonian astronomers was to discover periodic relationships for the various celestial phenomena in which they were interested, to enable these to be predicted as accurately as possible (i) for the purposes of omen astrology and (ii) for the improvement of the Babylonian calendar, which remained at all periods a strictly lunar one, each month beginning with the appearance of the lunar crescent. The phenomena in question are mainly horizon phenomena (except for eclipses and the ‘stations’ of the planets) (...) There is no trace in Babylonian astronomy (as at present known) of any desire to construct a comprehensive, mathematically based scheme which would account for all astronomical phenomena, or to investigate their nature and causes, or to take a synoptic view of the universe as a whole. (...) Thus the Babylonians never developed the concept of the celestial sphere or of terrestrial latitude and longitude, and hence many of the theoretical problems of establishing the correct relationships between the basic circles of the sphere (equator, ecliptic, horizon, and colures), which form a major part of Greek astronomy, never appear in Babylonian astronomy at all." (Early Greek Astronomy to Aristotle, Cornell University Press, 1970, pp.169-70). Acrescenta (p.176), que enquanto na astronomia babilónica se recorria a progressões aritméticas, a abordagem dos gregos será a do movimento circular e, a partir de Eudoxo de Cnido (Eúdoxos ho Knídios), à exploração das propriedades matemáticas do círculo e da esfera na explicação dos movimenos celestes.

Esta crítica é pertinente mas não interfere com a aquisição de um acervo observacional valioso para os efemeredistas e para a agilização da capacidade de previsão dos fenómenos, mesmo sem as ulteriores potencialidades cosmológicas da astronomia grega.

Era uma astronomia que, nos seus primórdios, se preocupava mais com os pontos nos quais os astros se elevavam e desciam do que com as culminações. Os historiadores dividem por comodidade o longo percurso da astronomia da Babilónia em quatro períodos (seguimos a exposição de Jean-Pierre Verdet (Une Histoire de l'Astronomie, Éditions du Seuil, 1990)).

Do período denominado "Paleo-Babilónico" (a partir de 1800 a.C.) chegaram até nós alguns textos. Em primeiro lugar, a tabuínha cuneiforme mais antiga com conteúdo distintamente astronómico, oriunda de Nippur, sugere que o céu foi dividido em três zonas e que a estas áreas estavam associadas não apenas a estrelas e constelações mas também, o que é interessante, a séries de números em progressão aritmética, primeiro traço conhecido de uma das ferramentas matemáticas que permitiu que os babilónios descrevessem fenômenos periódicos. O segundo período estende-se de 1530 a 612, data da destruição da grande biblioteca de Nínive quando a cidade caiu nas mãos dos Medos. Abrange a dinastia Cassita e a sequente dominação Assíria. É em direcção ao final deste período que aparecem os primeiros registros sistemáticos de observações feitas pelos astrónomos ao serviço das cortes assírias: o mais famoso, Enuma Anu Enlil ("Quando Anu e Enlil...", de acordo com as primeiras palavras da sua solene introdução) é proveniente da biblioteca de Assurbanípal. Do terceiro período, denominado Neobabilónico, que vai de 611 a 540, possuímos um almanaque para o 37º ano do reinado de Nabucodonosor II (568 a.C.). Este almanaque já enfatiza os percursos da Lua e dos planetas: as conjunções com as estrelas (fixas) são cuidadosamente anotadas, bem como como as datas da primeira e última visibilidade. As zonas celestes, que anteriormente eram divididas em quatro partes nas quais o Sol viajava (três meses em cada) estão agora divididas em doze sectores convencionais de 30°. O quarto período é o da dominação Persa e continua na época Helenística. Os progressos são significativos e a tendência para a descrição matemática consolida-se. Mas temos de esperar pelos últimos três séculos antes da nossa era, nos reinados dos Selêucidas e dos Arsácidas, para que surjam os primeiros textos onde o estudo dos movimentos celestes se baseia em teorias matemáticas algebricamente elaboradas. Assim, em resumo, ao longo de milénio e meio os astrónomos da Mesopotâmia acumularam observações e desenvolveram teorias matemáticas que permitiram uma boa descrição empírica dos movimentos da Lua, do Sol e dos planetas, bem como da variação do comprimento dos dias e das noites.

Por fim, esta prestigiosa cidade, tantas vezes (com toda a justiça) associada à Astronomia, foi devorada pelos séculos:
“The temple of Jupiter Belus ["Esagila", o Templo de Bel] in Babylon is still standing — Belus was the discoverer of the science of astronomy; but in all other respects the place has gone back to a desert.” (Historia Naturalis, V1, 30, 121; trans. Rackham (1942, p.431)). Na época de Trajano, em 116 AD, a Babilónia já estava abandonada.

"The gyre of the heavens, perfectly round at every point, is bound by the line of the zodiacal circle, like the discrete settings of twelve gems adjacent to each other on a sort of girdle wrapped around a very large sphere." (Wallis, Faith [ed./trans.], Bede: The Reckoning of Time, Liverpool University Press, 1999, p.55). Segundo Wallis, esta imagem pode basear-se nas doze jóias colocadas nos alicerces ("fundamentos dos muros") da Nova Jerusalém (Apoc. 21.19-20), relacionadas com os doze portões da cidade, voltados, três a três, para as quatro direcções cardeais (ibid. 21.13).

Seguimos a partir daqui uma recente exposição de Gennady E. Kurtik (On the origin of the 12 zodiac constellation system in ancient Mesopotamia, Journal for the History of Astronomy. 2021, Vol. 52(1) 53–66):

A origem do Zodíaco foi precedida pela criação de um sistema de constelações que ocupava praticamente todo o céu observável. Foi ainda precedida pela constatação da existência, para além do Sol e da Lua, de uma categoria especial de "estrelas" (que conhecemos como planetas). No período Babilónico Antigo (séculos XIX-XVI a.C.), aparentemente já existia um sistema de constelações praticamente completo. [Convém recordar que os povos da Mesopotâmia observavam e registavam os fenómenos mas não conceptualizavam uma "esfera celeste" com os seus grandes círculos; a ênfase "tridimensional" e geométrica será apanágio da abordagem grega]. Há muitos textos, datando até ao 2º milénio a.C. que mencionam nomes de constelações. Todavia, nenhum apresenta qualquer vestígio de que o conceito de "zodíaco" fosse conhecido neste período. A situação muda no período Neo-Assírio (séculos X-VII a.C.). A definição de uma faixa de constelações é encontrada pela primeira vez de modo explícito no sistemático acervo MUL.APIN de listagens astronómicas. Um deste textos (I iv 31–39) descreve 18 constelações que a Lua atravessa no seu percurso mensal. Quase todas são já conhecidas de textos pretéritos. São descritas sequencialmente, i.e. de acordo com o incremento da sua longitude (regra nem sempre escrupulosamente observada). Analisando outros textos, conclui-se que os astrónomos da Mesopotâmia reconheceram pelo menos 22 constelações na faixa zodiacal no 1º milénio a.C. Depois de estabelecido o "caminho da Lua" (MUL.APIN II i 1‒8), seguem-se, separadamente, as definições dos "caminhos" do Sol e dos planetas. As fontes explicitam que esses "caminhos" relativamente ao fundo de estrelas são coincidentes, emulam o "caminho da Lua". Não restam dúvidas de que no período referido já se sabia que os todos esses percursos estavam confinados a uma estreita faixa das constelações. Contudo, não se conhecem referências explícitas em textos observacionais. No 1º milénio a.C. foi igualmente gizado um sistema de cerca de 40 estrelas (não uniformemente distribuídas) ao longo da faixa zodiacal. São hoje identificadas como "Normal Stars". Nos textos cuneiformes são designadas MUL.ŠID.MEŠ, lit. "as estrelas (para) contar". As listas encontradas incluem um total de 17 nomes de constelações (quase todas referidas na lista dos "deuses no caminho da Lua", dos MUL.APIN), necessárias para determinar as posições relativas e identificar essas estrelas no céu. Os babilónios conseguiam determinar longitudes zodiacais dos planetas (com uma aproximação de 1-2 graus) pela observação das distâncias angulares relativamente às referidas estrelas de referência cujas posições eram conhecidas (de Jong, T., A study of Babylonian planetary theory I. The outer planets. Arch. Hist. Exact Sci. 73, 1–37 [2019]). Um sistema de 12 constelações ao longo da eclíptica foi o que os gregos encontraram quando adoptaram o Zodíaco da antiga Mesopotâmia (entre finais do V e início do IV séc. a.C.). Como é que um sistema de cerca de 18 constelações se transformou no sistema de 12? A resposta, segundo Kurtik, está provavelmente disponível no texto do séc. V a.C. classificado como 'WA77824', no qual as 15 constelações situadas na faixa que será chamada 'zodiacal' são divididas em 12 partes, correspondendo aos 12 meses lunares (esquemáticos, de 30 dias, não envolvendo intercalações) do calendário mesopotâmico. Foram descartadas as constelações que tinham apenas uma pequena porção da sua 'figura' na faixa relevante para o percurso da Lua e restantes "estrelas especiais" (planetas). A partir daqui há duas teorias: segundo a primeira, defendida por Kurtik, o zodíaco matemático (de 360º, dividido em sectores de 30º), associado aos meses esquemáticos, foi definido e somente depois se associaram as 12 constelações; a segunda opinião presente na literatura especializada inverte esta sequência: foi introduzido um esquema de 12 constelações e somente depois a 'equalização' matemática foi aplicada (cf. L. Brack-Bernsen, The Path of the Moon, the Rising Points of the Sun, and the Oblique Great Circle on the Celestial Sphere, Centaurus, 45 (2003), p.17, n.1). Como os nomes dos signos e das constelações, por regra, coincidem, é difícil discernir nas fontes o que é que está especificamente a ser mencionado. Em todo o caso, no IV século a.C. o perene sistema 12 constelações zodiacais já estaria aparentemente bastante disseminado na Mesopotâmia.

Os astrónomos babilónicos introduziram, como vimos, a conhecida divisão zodiacal em doze partes ou sectores iguais, pois sem esta seria extremamente difícil assinalar comodamente e com um mínimo de consistência as posições da Lua e dos planetas. Todavia, como Elisabeth (Elly) Dekker refere (Illustrating the Phaenomena: Celestial Cartography in Antiquity and the Middle Ages, Oxford University Press, 2013, p.14), os historiadores divergem nas opiniões quanto à data da introdução desta divisão babilónica na Grécia. Todas as referências nos textos dos astrónomos mais antigos se baseiam nas constelações zodiacais, não nos signos. Como Bowen e Goldstein salientaram, tudo indica que o próprio Eudoxus (que estudaremos adiante) ainda não procedesse à divisão dos signos em sectores iguais: "The ultimate source of our knowledge of Eudoxus’ Phaenomena and Enoptron , does not support the claim that Eudoxus divided the ecliptic into 12ths and each of these into 30 degrees of arc but even suggests that he did not." (Bowen and Goldstein, ‘Hipparchus’ Treatment of early Greek Astronomy: The case of Eudoxus and the Length of Daytime’, Proceedings of the American Philosophical Society, 135, 1991, p. 245). De facto, o Zodíaco descrito por Aratus é delineado pelas doze constelações (incluíndo as "pinças" do Escorpião, futura Libra). Trata-se das constelações, não dos signos! A primeira referência aos signos resultantes da divisão em doze sectores iguais parece recuar a Autólico, (Αὐτόλυκος, Autolycus) de Pitane, séc. IV a.C., todavia não se referindo a estes arcos como unidades de 30º. Um dos problemas recorrentes é, sem dúvida, a confusão entre constelações e signos, intercambiavelmente designados pela mesma palavra grega. Um texto sobre as "ascensões" (Ἀναφορικός, os tempos ascensionais [dos signos]) de Hípsicles (Ὑψικλῆς, séc. II a.C.), constitui a mais antiga referência grega que chegou até nós a utilizar a divisão babilónica do zodíaco em 12 sectores de 30 graus cada. (Montelle, C. (2016), "The Anaphoricus of Hypsicles of Alexandria", in: Steele, John M., The Circulation of Astronomical Knowledge (The Ancient World, Time, Astronomy, and Calendars: Texts and Studies, 6), Leiden: Brill, pp.287–315). Também já utiliza, como Hiparco fará sistematicamente, as divisões em graus e minutos.

O nome do primeiro signo mesopotâmico era (transliterado) MUL.LÚ.ḪUN.GÁ: "o trabalhador agrícola", "jornaleiro", "jeireiro". A substituição deste por Aries (Κριός) poderá ter ocorrido na tradição babilónica tardia, através da associação a Dumuzi (i.e. Tammuz), divindade relacionada com a pastorícia (Rogers, John H. (1998). Origins of the Ancient Constellations: I. The Mesopotamian Traditions. Journal of the BAA, 108 (1). No ciclo Tammuz-Ishtar, a morte de Tammuz, a descida de Ishtar ao infra-mundo para o resgatar e o renascimento sazonal de Tammuz relacionado com o calendário pastoril e agrícola. No clássico Star Names and their Meanings (1899) R. Hickley Allen cita uma referência a "Athamas" por Columella (autor do séc. I), que Allen relaciona com o Tammuz ("The Only Sun of Life") do mito mesopotâmico (p.76). Todavia, Átamas é o nome de um rei, pai de Phrixus e Helle no mito do Velo de Ouro. Rupert Gleadow, The Origin of the Zodiac (Dover, 2001 [Jonathan Cape, London, 1968]), observa (em relação ao Carneiro) que não se tratando de constelação mesopotâmica, outrossim não seria egípcia por não se encontrar uma correspondência no sistema de decanos. Contudo, este autor inclinou-se para uma hipótese "egípcia", não relacionada com a sua futura posição zodiacal mas sim com a sua culminação aquando do nascimento (helíaco) da estrela Sirius. A partir do mapa do céu e de especulações relacionadas com a Precessão, refere uma 'Barca' ("Boat"), "um particularmente evidente emblema sagrado", e o 'Carneiro', ambos bem elevados no céu nesse importante momento do calendário no país do Nilo. Conclui afirmando que se aceitarmos a [sua] associação da 'Barca' com a constelação Pegasus (v. p.200), então o 'Carneiro' era definitivamente uma constelação egípcia (pp.212-13). Autores mais cautelosos asseveram que, em rigor, desconhecemos a origem de Aries (e.g., Bartel van der Waerden, Sonderabdruck aus "Archiv fur Orientforschung, Band XVI, Zweiter Teil (reimpr. Archive of Oriental Studies, vol. XVI, Part II), 1952, p.226).

As supostas constelações do Carneiro e da Barca no Ramesseum (Karl R. Lepsius, id. III, 170), segundo a interpretação de Rupert Gleadow (Op. cit., plate 19)

O Zodíaco era, desde a Antiguidade, percebido como uma faixa, o que mais tarde gerou peculiaridades e erros cartográficos, pois por vezes eram representados os limites dessa faixa e não a própria eclíptica a tocar os trópicos (tropikós, do Gr. τροπή [tropē], "girar" ou "mudar de direcção"). Geminus (séc. I a.C.) fornece o primeiro registo acerca da sua espessura, que seria de 12º. Nas "tabelas" de Ptolomeu sugere-se que seria de 20º.

Filosoficamente, o "círculo inclinado" (eclíptica) e o zodíaco estavam, na perspectiva aristotélica, intimamente relacionados com as mutações da natureza elemental, a geração e a corrupção, i.e. com o devir a que se assiste no mundo sublunar. No Tractado da Spera... tirada de latim em linguage[m]..., (Lisboa: Germam Galhard[e], [ca. 1516]), escreve-se: "Este circulo em latim se chama signifero: porque nelle estam os signos. Aristoteles no segu[n]do de generatione lhe chama circulo torto. donde diz que segu[n]do do acesso: e recesso do sol no circulo torto se faze'a geeraçam: e corruçam das cousas."

Quanto à consequente correlação com o tempo, Beda, "o Venerável" (672/3 - 735) descreveu admiravelmente o círculo do ano materializado no Zodíaco:

"Signa duodecim vel a causis annalibus, vel gentilium fabulis nomina sumpserunt. Num Arietem Martio mensi propter Ammonem Jovem tribuuunt; unde et in ejus simulacro arietis cornua fingunt; Taurum Aprili, propter eundem Jovem, quod in bovem sit fabulose conversus; Castorem et Pollucem maio, propter indigne virtutis; porro Cancrum Junio, quando sol ad inferior redit, quia Cancer impulsus retro cursum dirigere soleat; Leonem, quem occidit Hercules, Julio, propter vim fervoris assignant; Virginem Augusto, quod tunc exusta caloribus tellus nihil pariat; Libram Septembri, ob aequalitatem dei et noctis; Scorpium et Sagittarium equinis cruribus deformatum, propter flumina mensium ipsorum, October et November accipiunt. Capricornum December propter capram Iovis nutricem, cuius extrema pisci similia pinguntur, quod huius mensis ultima sint pluvialia. Aquarium Ianuario, Februario Pisces, ob menses imbriferos tradunt. Singulis autem signis XXX partes, ternae vero decades deputantur, eo quod sol XXX diebus et decem semis horis illa percurrat, a medio mensis, id est, XV Kalendarum die, semper incipiens." (De Natura Rerum, Caput. XVII)

Quanto ao simbolismo bíblico, as interpretações poderiam associar os signos zodiacais aos doze profetas ou dos apóstolos. Antes, a correspondência com as tribos de Israel também seria evidente. Numa exegese Cristã, Aries poderia representar o "Agnus Dei", Virgo a "Virgem Maria", Libra seria, obviamente, a "Justiça", Leo o "Leão de Judá" enquanto Messias (Apoc. 5, 5: Não chores; eis aqui o Leão da tribo de Judá, a raiz de David, que venceu, para abrir o livro e desatar os seus sete selos.), Aquarius a "Água da Vida" (noster Aquarium), Pisces seria o próprio Cristo (ichthys ou ichthus: "o peixe"). Taurus podia ter um simbolismo sacrificial, Scorpio admoestava para o perigo das tentações (v. Lucas 10, 19: "Eis que vos dou poder para pisar em serpentes e escorpiões...", Capricornus e Sagittarius poderiam representar o próprio Diabo. Gemini poderia constituir uma alegoria dos dois Testamentos (o Antigo e o da "Nova Aliança"), o que se encontra na iconografia. Teresa Pérez-Higuera (Calendarios Medievales: La representación del tiempo en otros tiempos, Encuentro Editorial, 1997) refere (p.92 et seq.) diversas destas referências na iconografia e na literatura moralista, destacando um revelador sermão de S. Zeno (ou Zenão) de Verona (Zeno Veronensis, séc. IV).

Para além destes exemplos, podemos referir a muito mais antiga e confusa "mitologia sideral" quiliástica, principalmente relacionada com a interpretação dos textos apocalípticos, bem como todas as outras nascidas no âmbito de seitas cristãs gnósticas dos primeiros séculos, como os chamados "Ofitas" (que valorizavam a "benevolente" serpente do Éden enquanto fonte do Conhecimento). O ecletismo da época gerou prolixas narrativas envolvendo as constelações.

A iconografia sagrada, frequentemente encontrada nas representações dos Evangelistas, remete para os quatro "Viventes" constelados de olhos do Apocalipse (4 ,7): "E o primeiro animal era semelhante a um leão, e o segundo animal semelhante a um bezerro, e tinha o terceiro animal o rosto como de homem, e o quarto animal era semelhante a uma águia voando". Remetem para uma visão de Ezequiel e a primeira correspondência parece surgir em S. Ireneu (Adversus haer., 3.11.8) no séc. II. A associação com quatro signos zodiacais separados 90º entre si constitui uma interpretação interessante: o Leão (S. Marcos), o Touro (S. Lucas), o Aquário enquanto figura humana ou Anjo (S. Mateus) e a Águia (S. João), v. Richard Hennig, "Die Tyersymbole der vier Evangelisten", in: Wo lag das Paradies? Rätselfragen der Kulturgeschichte und Geographie, Verlag des Druckhauses Tempelhof, 1950, p.125 et seq.) [livro publ. em Portugal nos anos 70 como "Os Grandes Enigmas do Universo"]. Atendendo ao lento movimento de precessão, estes quatro signos assinalaram numa época remota o início das quatro estações, com Taurus no equinócio vernal. Na (discutível) interpretação que Hennig apresenta, a Águia substitui o Escorpião, considerado animal verminoso e perigoso. Segundo uma perspectiva teológica mais "convencional", o Leão podia ser o Princípio, com o seu rugido, representando João Baptista no deserto, o Touro remetia para os sacrifícios no Templo e para o sacerdócio de Jesus, o Homem para a genealogia de Jesus e a Águia simbolizaria a divindade, a dimensão contemplativa e o Verbo.

Equinócios e solstícios ca. 3000-750 a.C., segundo o orientalista Alfred Jeremias (Das Alter der babylonischen Astronomie, Leipzig: J.C. Hinrichs, 1916, p.55). O Touro ("Stier") assinalava o equinócio vernal.

Numa "Refutação de todas as Heresias" (obra conhecida como Philosophumena), de autor desconhecido (foi atribuída a Orígenes e, mais tarde, principalmente a Hipólito de Roma, séc. III), testemunhamos a lamentosa convicção do autor de que a exegese cristã estava impregnada de simbolismo astrológico, "adulteração" que atacou vigorosamente. [N.B. o A. confunde amiudadamente as 'autoridades' e as citações. No excerto seguinte cita Arato (Άρατος, Aratus) mas também lhe atribui ideias descontextualizadas e anacrónicas que seriam, obviamente, completamente alheias ao autor dos Phainómena]. Vejamos esta curiosa interpretação "herética" do mapa celeste, uma representação, como o seu moderno editor referiu, do "esquema Cristão da Salvação":

"(...) For in six days the earth came into being and there was rest on the seventh. If, then, he says, Adam making confession and guarding the head of the Beast according to God’s decree, will imitate the lyre [Lyra], that is, will follow the word of God, which is to obey the Law, he will attain the Crown [Corona] lying beside it. But if he takes no heed, he will be carried downwards along with the Beast below him, and will have his lot, he says, with the Beast. But the Kneeler ["engonasi", ulterior Hercules] seems to stretch forth his hands on either side and here to grasp the Lyre and there the Crown (and this is to make confession), as is to be seen from the very posture. But the Crown is plotted against and at the same time drawn away by another Beast, Draco the Less, who is the offspring of the one which is guarded by the foot of the Kneeler. But (another) man stands firmly grasping with both hands the Serpent [Serpens], and draws him backwards from the Crown, and does not permit the Beast to forcibly seize it. Him calls Serpent-holder [Ophiuchus], because he restrains the rage of the Serpent striving to come at the Crown. But he Aratus, he says, who in the shape of man forbids the Beast to come at the Crown is Logos, who has mercy upon him who is plotted against by Draco and his offspring at once. (...) And these Bears [as duas Ursas], he says, are two hebdomads, being made up of seven stars each, and are images of the two creations. For the First Creation, he says, is that according to Adam in his labours who is seen as the Kneeler. But the Second Creation is that according to Christ whereby we are born again. He is the Serpent-holder fighting the Beast and preventing him from coming at the Crown prepared for man. (...) But this Bear [Ursa Minor] he says is Cynosura [lit. "cauda do cão", nome usado, por exemplo, por Arato e Ovídio], the Second Creation, the small, the narrow way and not Helica [Helike=Ursa Majoris]. For she leads not backwards, but guides those who follow her forwards to the straight way, being the (tail) of the dog. For the Logos is the Dog (Cyon) who at the same time guards and protects the sheep against the plans of the wolves, and also chases the wild beasts from creation and slays them, and who begets all things." (F. Legge (ed.), Philosophumena or the Refutation of all Heresies, London: Society for promoting Christian knowledge, Macmillan Company, 1921; vol. I, Book IV, ch. 6: "Of the Divination by Astronomy", pp.110-112)

Ou seja, as duas Ursas, cada uma com sete estrelas, símbolizam as duas "criações": antes (Ursa Major) e depois (Ursa Minor), sendo a segunda o Advento de Cristo. O Cão (Cynosura) é a Palavra; o Dragão o próprio Diabo. A constelação a que se chama Engonasi ("ajoelhado") representa Adão penitente, estendendo uma mão em direção à Lira (instrumento do Logos, da Palavra), a outra em direção à Coroa (Corona); enquanto o Serpentário (Ophiuchus, Lat. Anguitenens), que segura a Serpente (como o nome indica), impede que o Dragão possua a Coroa, que está destinada ao Homem. Na sequência, o autor continua a expor interpretações similares tendo como pretexto outras constelações (por exemplo as que se integram na épica de Andrómeda, onde o Logos será Perseus). E protesta: "Making use of these discourses, they think to deceive as many as give heed to the astrologers, seeking therefrom to set up a religion which appears very different from their assumptions.".

No Egipto utilizava-se um sistema numérico decimal. O ano civil era convencional, não astronómico. Tinha 360 dias, divididos em 12 meses de 30 dias cada. Considerava-se ainda 5 dias 'extraordinários', "epagomenais" (na designação grega), aproximando este calendário do solar 'verdadeiro'. Simples, independente dos complexos movimentos lunares, de intercalações e circunstâncias "ad hoc" locais de aplicação das mesmas. "The only intelligent calendar which ever existed in human history", segundo Otto Neugebauer (The Exact Sciences..., p.81). Observava-se o nascimento helíaco de Sirius (personificado pela deusa Sopdet, Sothis) para determinar o início do ano, concomitante com o da estação da cheia fertilizadora do rio Nilo. O seu aparecimento também regulava o antigo calendário lunar que, curiosamente, iniciava os meses com a última observação do minguante (antes do novilúnio) no horizonte leste.

Em tempos recuados verificou-se que quando o Nilo começava a incrementar o seu caudal em Mênfis (então a capital), a estrela Sirius surgia pela primeira vez de manhã no horizonte leste (nascimento helíaco). Aconteceu assim, na terceira década do mês que equivale a Junho, até cerca de 2000 a.C. Devido à precessão, em 1000 a.C. o nascimento da estrela já se verificava somente em meados de Julho, perdendo o seu carácter anunciatório (Pannekoek, A History of Astronomy, Interscience Publishers & George Allen and Unwin, 1961, pp.83-4). Mas o simbolismo permaneceu. Recordemos o versejar vitoriano de Sir Edwin Arnold (The Egyptian Princess):

Em cima, um primitivo instrumento de visada e levantamento topográfico chamado bay pelos egípcios. Possuía uma ranhura e podia ser utilizado em conjunto com o instrumento menor em forma de "L", o merkhet, que teria um fio de prumo que marcaria a vertical (v. esquema; Magdolen, D., An Astronomical Inscription on the Berlin Merkhet, "Asian and African Studies", 10, 2001, 1, 80-87), útil na materialização do meridiano e na determinação das horas a partir das estrelas culminantes. O merkhet poderia também ser usado como gnómon para observar as sombras durante o dia. Este foi feito em osso, com um braço horizontal com apenas 11.5cm de comprimento. Ambos os instrumentos datam de c.600 a.C. (Ägyptisches Museum und Papyrussammlung, Berlim; No. 14084 e 14085). Verificou-se, todavia, alguma ambiguidade na definição deste instrumento na literatura especializada, v. excerto relevante de Zbynek Zaba (L'Orientation Astronomique dans L'Ancienne Égypte, et la Précession de l'Axe du Monde, Ceskoslovenská Akademie Vêd - Archiv Orientální - Suplementa; II (1953); em Francês)

Como não utilizaram o equivalente ao ano "bissexto" antes da reforma do calendário promovida na época romana, o desfasamento de 1 dia em cada 4 anos fazia com que demorassem 1460 anos (tropicais, equivalendo a 1461 anos egípcios) para a coincidência do nascimento helíaco de Sirius (Sopdet, Gr. Sothis) com o início do ano solar. Era o "Período Sotíaco" ou Canicular, que pode ter tido relevância cronológica (sendo mais provável que nem sequer fosse considerado e que toda a sua importância tenha sido inventada muito mais tarde, ex post facto). Em paralelo, manteve-se um calendário lunar (com meses de 29 e 30 dias), mais antigo, onde se intercalava, em alguns anos, um mês (Thoth), para compensar a diferença para o calendário solar. Dividiram o círculo anual em 36 "decanos" (de 10º cada). Também encontramos a influência egípcia na divisão do Dia em 24 horas (primeiro sazonais e, na astronomia helenística, equinociais, i.e. de igual duração, utilizando o sistema numérico sexagesimal proveniente da Babilónia). Muito mais tarde, os "anos persas" da Era de Yazdigerd (começo em 632 A.D., Yazgederg III foi o último soberano independente antes da anexação islâmica da Pérsia), também baseada nos anos egípcios, será uma referência em tratados astronómicos Islâmicos e Bizantinos. No sistema de decanos egípcio, determinados asterismos (funcionando como "marcadores") sucediam-se a cada 10 dias e cada dia nasciam 4 minutos mais cedo. Estabeleciam intervalos de 12 durante uma noite e de 10 dias ao longo do ano. Verificava-se qual o asterismo que nascia mais próximo da aurora. O sistema observa-se nos chamados "calendários diagonais" representados em túmulos, assim chamados pois no seu desenho cada decano sobe uma linha, de uma coluna para a seguinte. Balizavam as horas e revestiam-se, tradicionalmente, de atribuicões simbólicas, auspiciosas ou adversas. Terão influência na doutrina astrológica, talvez até no próprio conceito de 'hōroskopos' (ωροσκόπος, o "ascendens") e em geral, nos quatro 'ângulos' da chamada figura.

As ilustrações astronómicas tumulares (patentes a partir do Império Médio) são representações do céu, com os nomes das constelações dos decanos (ou 'decanatos') alinhados, como referido, em intervalos de 10 dias ao longo do ano, formando assim 36 colunas de 12 linhas, uma para cada uma das 12 horas da noite. A partir de um coluna para a seguinte, o nome de cada decano sobe uma linha. O que dá uma estrutura diagonal que lhe valeu o nome (inadequado) de "calendário diagonal", embora seja um relógio estelar. Essa representação diagonal permitia saber a hora da noite: bastava procurar o decano que "subia" na coluna da década (período de dez dias) em causa.

Detalhe de um calendário estelar 'diagonal' na tampa de um caixão da XIª Dinastia (2134-2061 a.C.), em Asyut (commons.wikimedia.org)

Anne Sophie von Bomhard, na monografia The Naos of the Decades: From the Observation of the Sky to Mythology and Astrology (Centre for Maritime Archaeology, Oxford, 2008), apresenta, a partir da articulação de evidèncias resultantes de investigações subaquáticas e descobertas recentes em Canopus, argumentos para a utilização um sistema de "decanos" com significações apensas que parece indiciar a presença de uma tradição mais antiga (pré-helenística) de astrologia especificamente egípcia.

A interpretação simbólica relacionada, de dias auspiciosos e nefastos, decerto antiga, vai determinar uma forma de prognosticação que mais tarde vamos encontrar nos calendários medievais: é a listagem dos nefastos ou dies Aegyptiaci (assim designados pelo menos desde o século IV). Atentar na etimologia de "aziagos", lat. aegyptiacus, gr. aiguptiakós (in Dicionário Priberam da Língua Portuguesa [em linha]). Os dies atri romanos estavam presentes pelo menos desde a época de Augusto. Supunha-se que os "dias egípcios" (habitualmente 24, dois por cada mês), teriam sido sinalizados por "veneráveis astrólogos egípcios" ou então representavam os dias em que calamidades se haviam abatido sobre o país atravessado pelo Nilo, referência provável às célebres pragas bíblicas), Chamaram-lhe dies mali, maledicti, ominosi, infortunati ou tenebrosi. Evitavam-se empreendimentos e procedimentos médicos, como as purgas. Com o tempo, cada um destes dias foi associado a uma hora dita mala, timenda, aegra ou suspecta (vide Skemer, D., 'Armis Gunfe': Remember Egyptian Days, Traditio, Vol. 65, Fordham University, 2010, pp. 75-106)

Em relação às contelações indígenas da "abóbada" egípcia, J. Lull e J.A. Belmonte (Egyptian Constellations, in C.L.N. Ruggles (ed.), "Handbook of Archaeoastronomy and Ethnoastronomy", Springer, 2015, vol.3, Part IX, ch. 130). publicaram esta tabela (.PDF, 544KB) que resume os casos em que os autores consideram a identificação "altamente segura".

Os asterismos e estrelas circumpolares (que para os egípcios era "imortais" ou "invencíveis", pois não tinham ocaso, não "morriam") eram extremamente importantes pelo seu simbolismo. Quanto às restantes estrelas fixas:

"In a simplified scheme of 360 days, we are informed that a star dies and a star lives every 10 days. After 70 days of death in the Duat [período de invisibilidade] a star is born again. It then spends 80 days in the eastern sky before it works, after which it passes 120 days (10 for each hour) telling time by its transit. When it has finished marking the 1st hour it passes 90 days in the western sky and then again it dies. Since a star spends 80 days in the east before working, it is clear that it is transitting" (R. A. Parker, "Ancient Egyptian astronomy", in: F. R. Hodson (ed.), The Place of Astronomy in the Ancient World, Op. cit., 1974, p.56).

Entretanto, a deusa Nut personificava o arco celeste e talvez possa estar paralelamente relacionada com a Via Láctea.

Shu (no centro) suportando a deusa do arco celeste, Nut, com Geb, deus da terra, a seus pés. Detalhe do papiro Greenfield, décimo séc. a.C; Museu Britânico

Numa interpretação fascinante, acredita-se que um dos mais relevantes aspectos do simbolismo da deusa Nut esteja relacionado com a vasta mancha da Via Láctea e o percurso do Sol como era observado do Vale do Nilo no início do Império Antigo (e desde a época Pré-Dinástica). Versão antropomórfica da Via làctea, Nut assistia a transformação do "Omnipotente" Rá (o Sol), no seu percurso através do calendário. Os Solstícios seriam pivotais, particularmento o de Inverno, quando o Sol "nasce", como que emergindo do ventre da deusa, canal representado pela região bifurcada da galáxia (em Cygnus) observável no horizonte oriental bem cedo (na época de referência, c.3500 a.C.); vide Wells, R.A., The Mythology of Nut and the Birth of Ra, Studien zur Altägyptischen Kultur, Bd. 19, pp. 305-321 (publ. Helmut Buske Verlag GmbH). Na imagem: representação moderna da Via Láctea observada de latitude norte (Ronald Wells, Astronomy in Egypt, in Walker, C. (Ed.), Astronomy Before the Telescope, BCA, 1996)

No resumo simplificado de Colin Ronan: "The Babylonians first made observations, next devised mathematics to describe what happened, and only then started to think about how this could be theoretically explained. (...) The Greek approach was almost completely the opposite—having recognized that planets move, they then constructed a theory; only after this did they observe the motions in detail and adjust thetheory to correspond. (Discovering the Universe, A History of Astronomy, Basic Books, Inc., Publishers, 1971, p.22)

A Astronomia grega nasceu com a organização das estrelas em constelações tendo como incentivo preocupações calendáricas e o conhecimento dos nascimentos e ocasos. Esta tradição será consolidada nos parapegmata (que devolviam informação de "almanaque" dos fenómenos cíclicos, sazonais) e presidiu à estrutura d'Os Trabalhos e os Dias de Hesíodo. Podemos ainda ter uma ideia da estrutura primitiva grega do mundo seguindo Homero na sua descrição do 'Escudo de Aquiles', no oitavo livro da Ilíada (483-89; cf. viii, 13-16; Od. i, 52-4. A cultura grega acrescentará (tradicionalmente a partir de Tales de Mileto, IV séc. a.C.), uma concepção naturalista da explicação dos fenómenos e também o conceito de Kósmos organizado e interdependente, que enformará doutrinas sequentes. Preocupações filosóficas e cosmológicas e a dinâmica e natureza da matéria primordial ocuparam os chamados "Físicos Jónicos", aos quais Aristóteles de Estagira (384-322 a.C.) chamou physiologoi, i.e. "os que discursam sobre a natureza", que apenas conhecemos através das referências indirectas que outros fizeram das suas elucubrações.

Os Pitagóricos deram ênfase a uma leitura qualitativa dos números e à geometria. Platão, influenciado por esse "misticismo numérico", descreverá nos seus diálogos toda uma influente cosmologia e ciclologia (e.g., o 'Grande Ano' ou 'Ano Perfeito').

Os gregos usavam letras do seu alfabeto para representar os numerais. A inicial "ο" de οὐδέν (i.e. "nada") era utilizado como mais tarde será o zero.

Os Pitagóricos parecem ter subordinado os factos e os fenómenos naturais às suas predilecções filosóficas e místicas. Um exemplo da sua mundividência é a concepção de um "fogo central", relegando surpreendentemente a Terra para um estatuto no qual simplesmente revolve em torno desse fogo, tal como as restantes estrelas errantes e fixas. Talvez as descobertas tradicionalmente atribuidas ao próprio mestre (os principais intervalos musicais: oitava, quarta, quinta, expressos através de rácios numéricos de 2:1, 4:3, 3:2, bem como o facto de os primeiros quatro somarem 10, o "número místico" ou "tetractys"; o célebre Teorema de Pitágoras, etc.) tenham potenciado a crença no Número enquanto entidade fundamental do universo. (Dicks, p.65). As suas ideias são, portanto, fruto dessas elucubrações, baseadas no primado do número, na simetria e na harmonia. A influência em Platão é evidente mas Aristóteles será céptico e, por exemplo, considera absurda essa "harmonia sonora universal":

"Very little astronomical sense is apparent in another feature of the Pythagorean scheme, the famous ‘harmony of the spheres’. According to Aristotle (De Caelo ii, 9, 290b 12f. = DK* 58 B35), an absurd and extravagant opinion (his own words) was held by the Pythagoreans, to the effect that, with so many huge celestial bodies whirling at such great speeds round the centre, it was impossible that no noise should be generated by their motions, but each body must produce a different tone according to its distance from the centre, so that the whole system created a ‘harmony’. An ingenious explanation was given of the awkward fact that no one ever hears this harmony, namely that everyone, from the moment of birth, has this sound as a constant background and therefore does not consciously hear it, since there is no absolute silence to contrast with it. This poetic fancy (presumably suggested by the discovery of the ratios governing the chief musical intervals) was taken up by Plato in the myth of Er in Republic X, and further elaborated by later writers who invented all sorts of musical schemes supposed to represent the proportionate distances of the heavenly bodies." (Dicks, D. R., Early Greek Astronomy to Aristotle, Op. cit., p.71)

* DK: H. Diels, Die Fragmente der Vorsokratiker, 6th ed., revis. W. Kranz, 1951-52.

As cordas do "heptacorde celeste" pitagórico revelariam, pela harmonia dos seus tons, as distâncias entre os planetas (G. Bigourdan, L'astronomie: évolution des idées et des méthodes, Paris: E. Flammarion, 1920 [1911], p.49)

A concepção da "música das esferas" incorporava o princípio metafísico de que as relações matemáticas exprimiam qualidades ou "tons", sons e números relacionados segundo um padrão de proporções. A existência de uma harmonia divina e matemática entre o macrocosmo e o microcosmo. A Música era proporção. A Anima Mundi (psyché tou pantós) é outro conceito plat ónico fundamental: força regente do Universo, que o envolve, pela qual o pensamento divino se pode manifestar em leis que afectam a matéria, ou ainda, uma força imaterial, inseparável da matéria, mas que a provê de forma e movimento. Foi exarada pelo filósofo n'A República, no Timeu e no livro X das Leis. Considerada como o princípio do Universo e fonte de todas as almas individuais. Aquando da sua criação, a Anima começou a girar e este foi o início da "vida inextinguível e racional" (Timeu, 36-e). O Cosmos vivo e animado de Platão foi criado segundo princípios matemáticos e rácios pitagóricos (inferidos das harmonias musicais). Os arquétipos transcendentes e ideais governavam o mundo da Natureza. O Timeu refere o movimento das estrelas e planetas como "a dança dos deuses". Quanto à estrutura cosmológica do Universo, o filósofo utiliza a esfera armilar como metáfora para a Criação do Universo (34-b–36-e). Eis alguns excertos relevantes do influente tratado (trad. Rodolfo Lopes; Coimbra, 2011):

"...Então, [o Demiurgo] cortou toda esta composição em duas partes no sentido do comprimento e, sobrepondo-as, ao fazer coincidir o centro de uma com o centro da outro (semelhante a um X) dobrou-as em círculo, juntando-as uma à outra pelo ponto oposto àquele pelo qual tinham sido ligadas, e impôs-lhes aquele movimento circular que gira no mesmo local; destes dois círculos, fez um exterior e outro interior. Então, determinou que o movimento exterior corresponderia à natureza do Mesmo, e o interior à do Outro. Fez com que o movimento do Mesmo se orientasse para a direita, girando lateralmente, e que o do Outro se orientasse para a esquerda, girando diagonalmente, e deu preeminência à órbita do Mesmo e do Semelhante, pois a ela só deixou ficar indivisa. Por outro lado, a órbita interior dividiu-a em seis partes e formou sete círculos desiguais, fazendo corresponder cada um deles a um intervalo duplo ou triplo, de tal forma que havia três tipos de intervalos. Definiu que os círculos andariam em sentido contrário uns aos outros, três dos quais com velocidade semelhante, e os outros quatro com velocidade diferente uns dos outros e dos outros três, mas movendo-se uniformemente," (36-b-c-d)

"...a órbita do Outro, que, por ser oblíqua, atravessa a órbita do Mesmo e é dominada por ele. Alguns astros deslocam-se em círculos maiores, e outros em círculos mais pequenos; os que estão nos círculos mais pequenos deslocam-se mais rapidamente e os que estão nos círculos maiores deslocam-se mais lentamente. E por causa da órbita do Mesmo, parecia que os que se deslocavam mais rapidamente eram alcançados pelos que se deslocavam mais lentamente, quando eram aqueles que alcançavam este." (39-a)

"Em todo o caso, é pelo menos possível perceber que o número perfeito do tempo preenche o ano perfeito cada vez que as velocidades relativas da totalidade das oito órbitas, medidas pelo círculo do Mesmo em progressão uniforme, se completam e voltam ao início." (39-e)

Ou seja, o Demiurgo de Platão construiu duas armilas ou anéis, com um centro comum (a Terra), numa esfera em que a armila, anel ou Círculo da Igualdade (ou "do Mesmo") é associado ao Equador Celeste (sendo responsável pelo que designamos movimento primário ou diurno) e o Círculo do Diverso ("da Diferença" ou "do Outro") equivalendo à Eclíptica, que foi dividido de modo a alojar as órbitas dos planetas. A diferença entre os dois planos corresponde à obliquidade da Eclíptica. Eis o que estes círculos, entre outras coisas, representam. O Círculo da Igualdade é considerado "exterior" pois é esse que controla o outro, bem como representa a esfera exterior (onde foram fixadas as estrelas). Em 39-e temos a alusão ao conceito do Ano Perfeito, quando os ciclos das órbitas se sincronizam e completam, i.e. quando os planetas voltam a um mesmo ponto do céu ao mesmo tempo. Aristóteles também ensinará que os movimentos eternos e regulares dos astros são impelidos pela 'vontade' e pela 'inteligência'. Antes, como vimos, havia formulado (De generatione et corruptione) a doutrina de que os movimentos nos céus eram a primeira causa de mudança na Natureza.

Um conhecido comentário na República (530b-c) evidencia a postura de Platão e a sua suposta escassa promoção do conhecimento astronómico e das ciências experimentais em geral. Na interpretação mais frequente, o orador Sócrates pretende que se privilegie a base teorética apriorística e que se investigue o aspecto matemático e relações subjacentes, em detrimento do acumular empírico de informação baseada nos fenómenos. Reflecte a influência pitagórica e a dicotomia platónica entre a verdade das ideias versus as aparências. O contexto em que surge é o da discussão de um "currículo" para uma educação "ideal". A mesma tendência se pode verificar em toda a sua metafísica: o primado do intelecto e a profunda desconfiança relativamente aos que percebemos através dos sentidos.

Quatro Elementos - Bartholomaeus Anglicus

Representação dos quatro Elementos no enciclopédico De Proprietatibus Rerum, Bartholomaeus Anglicus, 1491. Nas Leis (x, 889b), Platão explica com brevidade como alguns autores (tendo seguramente em mente Empédocles de Agrigento) acreditavam que todo o céu e tudo debaixo deste eram produzidos pela combinação de quatro elementos, operando de modo natural e contingente e não segundo pressupostos ou um plano divino (ressalva que contrariava a mundividência platónica onde os corpos celestes eram investidos de alma e considerados divinos). No platonismo, os quatro elementos de Empédocles são associados aos cinco poliedros regulares. O quinto, o dodecaedro, simboliza o Cosmos como um todo.

De facto, na Grécia, a vertente teorética prevalecerá sobre a observacional ("...the priority and reliability of cognitive inference over visual evidence ", Montelle, Op. cit., p.19), como Sócrates (i.e. Platão) também expende no Fédon:

«Depois disto, uma vez desiludido da observação dos seres, achei por bem acautelar-me, não viesse a acontecer-me a mim o mesmo que àqueles que contemplam e observam o Sol em momentos de eclipse: é sabido que alguns chegam a perder a vista, se não é através da água ou de qualquer outro meio que observam a sua imagem. E, com pensamentos mais ou menos deste teor, receei ficar irremediavelmente cego de espírito, caso persistisse em fixar os olhos nas coisas, em tentar tocar-lhes directamente com os meus cinco sentidos. Pensei então que o melhor que tinha a fazer era refugiar-me do lado das ideias e, através delas, inquirir da verdade dos seres. Aliás, talvez num aspecto o paralelo não seja exacto, pois não é, quanto a mim, ponto assente que o estudo dos seres, através das suas manifestações externas, se revele, menos do que através das ideias, um estudo à base de imagens...»
(Fédon, 99d-e, [Maria Teresa Schiappa de Azevedo, ed.], Coimbra: Livraria Minerva, 1988, p. 106)

Passagem tornou-se polémica, tal como a previamente citada da República, pelo aparente "desprezo" do sage pela observação empírica e experimental. A razão parece ser profundamente filosófica mas segundo Clemency Montelle, as limitaçóes observacionais do passado reforçaram, ironicamente, o investimento na vertente teórica. Elenca as contrariedades em presença:

"These challenges included those related to the method of observation and the equipment available for it and those related to the conditions under which the phenomenon is to be observed. Among the first category are included limitations of the human eye, nonstandardized forms of measuring equipment, the imprecision of timing devices such as water clocks, the fuzziness of the tip of a shadow cast from a gnomon, the finite diameters of slits and pins at instruments, and the difficulty of estimating very small angles, some effects being so small that they are impossible to measure directly or with precision, such as parallax, solstices, and stations and first and last visibilities of planets. Examples in the second category include weather, refraction, geographical challenges, and the reliability of testimony." (Chasing Shadows, Op. cit., p.17).

- Para uma discussão proficiente da estrutura "metamatemática" mais tarde erigida no início da Idade Moderna sobre fundações pitagórico-platónicas, v. Edward W. Strong, Procedures and Metaphysics: A Study in the Philosophy of Mathematical-Physical Science in the Sixteenth and Seventeenth Centuries (Berkeley: University of California Press, 1936), ch. VIII.

A Esfera Celeste

O conceito de Esfera Celeste e (provavelmente) o da esfericidade da própria Terra estabeleceu-se, entre os gregos, a partir do século V a.C. [N.B: a segunda é uma questão mais delicada. Foi atribuida a autoridades como Parménides mas trata-se de um equívoco pois é aí referência à esfera tão somente enquanto sólido do geómetra (Guthrie, W. K. C., A History of Greek Philosophy, Cambridge University Press, vol.ii, 49). A especulação que envolve os pitagóricos baseia-se numa inferência a partir do que se conhece das suas ideias. O próprio Platão é ambíguo (de facto, a forma da Terra não é mencionada, nem no Timeu nem na República). O primeiro autor que refere a esfericidade do planeta, sem qualquer ambiguidade, é Aristóteles no De Caelo. O resto são meras suposições.]

O desenvolvimento da astronomia teórica pode ser testemunhado (sempre indirectamente, acreditando na fiabilidade de compiladores e comentadores), pela criação de sucessivos modelos do Universo (alguns bastante peculiares, como o pirocêntrico do pitagórico Philolaus (Filolau), que incluia um fogo central (um "Fogo de Héstia") e uma anti-Terra, 'Antichthon', interposta, que o eclipsava (e por isso não o podíamos ver), ou o heliocêntrico, genericamente proposto por Aristarco de Samos (Αρίσταρχος ο Σάμιο), que lançou a sugestão que conhecemos através de uma referência no Αρχιμήδης Ψαµµίτης, Psammites ou 'Arenário', de Arquimedes (Lat. Archimedis Syracusani Arenarius & Dimensio Circuli) não disponibilizando um modelo funcional (vide prefácio de W. H. Stahl e p. 136 et seq. em A History of Astronomy from Thales to Kepler, de J. L. E. Dreyer, reimpr. Dover Publications, 1953). De resto, como Dreyer salienta, nenhum sistema filosófico anterior à época de Aristarco supôs qualquer possibilidade de uma influência poderosa emanando do centro, com excepção do suposto sistema de Philolaus. (...) De acordo com Aristóteles, numa esfera ou num círculo todas as influências emanavam da circunferência exterior (periférica), prosseguindo na direcção do centro (p. 146; [trad. nossa]). As ideias de Aristarco não são mencionadas por Copernicus porque só foram (re)divulgadas a partir de 1544.

Entretanto, a partir da construção conceptual da Esfera Celeste e da esfericidade do planeta, tornou-se possível relacionar a duração do comprimento do dia mais longo do ano (ou do dia mais curto) com a posição do Equador e dos Trópicos em relação a um horizonte local específico, e que por sua vez esta relação determinava a posição (i.e. latitude) do observador na circunferência da Terra). Determinará o conceito dos "climas" (klimata), faixas de latitude nas quais a sphaera será dividida. Mas trata-se de um desenvolvimento provavelmente mais tardio do que habitualmente se supõe. O rácio em horas entre o dia maior e o menor do ano define, grosso modo, o "clima" em que a localidade se situa.

Eudoxus

Eudoxus de Cnido (c.395-390 - c.342-337 a.C.) foi quem primeiro advogou a quantificação da informação observacional e o seu tratamento matemático. O seu modelo das esferas homocêntricas prevalecerá e será mesmo ampliado e justificado pela Física de Aristóteles, configurando um sistema finito, esférico e ordenado. Os argumentos de Aristóteles sobre o modelo de Eudoxo são apresentados especificamente no livro XII (conhecido como livro Λ, letra grega que o identifica) da Metafísica. A outra fonte histórica é encontrada num comentário ao de Caelo de Simplikios (Lat. Simplicius). A matemática e, posteriormente, a trigonometria (nomeadamente as cordas), estarão no centro dos desenvolvimentos (convém referir que o desenvolvimento da trigonometria não é anterior ao segundo século a.C., justamente a época de um dos seus fundadores: Hiparco, 190-120 a.C.).

Apesar de algumas especulações quanto à tábua Babilónica "Plimpton 322" e sugestões da presença de rudimentos de Trigonometria no chamado "Papiro de Rhind" ou "Ahmès" (Egipto, 1700-1550 a.C; British Museum 10057-8), foi na Grécia do século III a.C. que a Trigonometria adquiriu sistematização a partir da Geometria. A primeira tabela, supostamente construída por Hiparco, tinha por base uma única função que relacionava cada arco da circunferência com a sua respectiva corda. É a primeira abordagem científica. E Menelau de Alexandria (c. 100 a. C.), astrónomo e geómetra, escreveu um tratado sobre cordas.

Antes de mais, segundo Alan C. Bowen e Bernard R. Goldstein ("A New View of Early Greek Astronomy", Isis, vol. 74, No. 3 [Sep. 1983], p.333), o maior contributo de Eudoxus, acompanhando a transformação da Astronomia em ciência matemática, foi a criação do "modelo das duas esferas":

"By "model," we mean the mathematical analogy of the celestial and terrestrial spheres, an analogy which was exploited on the principle that the properties of one must correspond to the properties of the other".

Os autores concedem que estes elementos não eram novos, mas foi a primeira vez que foram utilizados no âmbito dos textos da Astronomia (e não em considerações cosmológico-morais). O "modelo de duas esferas" concêntricas, a terrestre e a celeste, representa uma analogia matemática entre ambas (v. pág. Esfera).

Eudoxus foi o principal responsável pela transformação da Astronomia numa ciência matemática, uma explicação matemática dedutiva de fenómenos físicos. Para Bowen e Goldstein, a sua inspiração residiu em duas fontes: a já estabelecida ciência musical, que analisava os fenómenos estéticos, os sons melodiosos, através de rácios de números inteiros. Em segundo lugar, propõem, pelas especulações cosmológicas, particularmente as Pitagóricas e as de Platão. Nestas, a circularidade dos movimentos dos astros manifestava uma ordem moral e harmonia relacionável, em última análise, com as proporções da Música. Harmonia e Número. Uma explicaçáo abrangente do "modelo" pode ser encontrada em Estrabão (Gheograficá, Lat. Geographia, 2.5.3, H. L. Jones, ed./trans., The Geography of Strabo (Loeb Classical Library, Harvard Univ. Press, 1917, Vol. I, pp. 425-427).

O sistema planetário de Eudoxus, que recorria exclusivamente a movimentos de rotação, baseava-se, num “epiciclóide esférico" a que Eudoxus chama hippopede ("hipópede", a figura em "8" que pode ser gerada por duas esferas concêntricas com eixos não coincidentes, termo que Xenofonte explica pela comparação com um exemplo da equitação, por analogia com o percurso que os cavalos faziam em exercício nas pistas de treino). Uma lemniscata esférica, como hoje diríamos. Na eterna distinção entre a "esfera matemática" explicativa de um movimento e o "orbe material" (corpóreo), nada sabemos do estatuto ontológico atribuído por Eudoxus às suas esferas. Acreditava que eram reais ou apenas um expediente conveniente?

Resumidamente utilizavam-se quatro esferas concêntricas para cada planeta. O eixo da primeira unia os pólos Norte e Sul e simulava o movimento diurno do planeta; a segunda estava colocada de modo a que o seu equador (o da esfera) coincidisse com o plano da Eclíptica, revolvendo de Leste para Oeste e reproduzindo no seu período de rotação o movimento médio do planeta no seu percurso completo ao longo do Zodiaco. As duas restantes esferas (rodando com a mesma velocidade em sentidos opostos), com eixos deferentes (com inclinações adequadas e específicas para cada planeta), acautelavam as estações (paragens) e retrogradações. Ler infra uma breve descrição do modelo.

Segundo Arthur Berry, Eudoxus procurou formular uma explicação "qualitativa", não uma explicação "quantitativa" que explicasse com precisão os movimentos observados: "There is no clear evidence that Eudoxus made any serious attempt to arrange either the size or the time of revolution of the spheres so as to produce any precise agreement with the observed motions of the celestial bodies, though he knew with considerable accuracy the time required by each planet to return to the same position with respect to the sun; in other words, his scheme represented the celestial motions qualitatively but not quantitatively." (A Short History of Astronomy, Dover Publications, 1961 [1898], p.28). De facto, o modelo representava os movimentos planetários mas não seria exequível através dele conhecer informação posicional relevante. Não conseguia replicar as fases mais críticas dos movimentos, nomeadamente as retrogradações. Também permitia uma reduzida amplitude para a escolha dos períodos planetários e, nessa época, ainda não se tinham desenvolvido as ferramentas de trigonometria esférica necessárias para extrair resultados numéricos (disponíveis somente dois séculos depois de Eudoxus). Há várias "reconstruções" matemáticas plausíveis mas alguns investigadores, como A. C. Bowen, colocam em causa a perspectiva e os conhecimentos existentes no séc, VI a.C., nomeadamente no que respeita às retrogradações e, consequentemente, algumas "reconstruções" (v. Bowen, A. C., Perspectives on Science 2, 10 (2002)). A opinião mais comum é a de que o modelo explicaria razoavelmente os fenómenos como Eudoxus os conhecia. Entretanto foram sendo descobertas outras complexidades. Infelizmente, segundo Simplicius, o sistema de Eudoxus não explicava as evidentes alterações cíclicas do brilho observado nos planetas em cada período sinódico, implicando que as distâncias destes variava ao longo desse período (contudo C.C. Carman coloca em causa este antigo argumento, v. Studies in History and Philosophy of Science 54, 90 (2015)). Na ausência de fontes originais, as reconstruções, como a de Schiaparelli (Le sfere omocentriche di Eudosso, di Callippo e di Aristotele, Pubblicazioni del R. Osservatorio di Brera in Milano, No. IX. Milano, 1875) não podem ser consideradas "definitivas" (H. Mendell, Centaurus 40, 177 [1998]).

A sistematização do observável conduziu ao modelo mais óbvio: o Geocêntrico, Este sobreviveu incontestado até muito tarde, tanto na Europa como em terras Islâmicas, por uma razão simples: apesar de algumas incongruências (compensadas na prática por estratagemas geométricos e de cálculo que abordaremos adiante), estava de acordo com os factos observados e com os dados disponíveis na época.

A abordagem prática grega, informada pela geometria e pela Teoria dos Elementos (aparentemente remontando ao siciliano Empedócles, séc. V a.C., que chamava "raízes" a cada um destes imutáveis), tornar-se-á resiliente a partir da monumental estruturação de Aristóteles. Como Dicks resume (Op. cit., p. 199), para Aristóteles o Universo é finito (De Caelo i, 5, 6 e 7), pleno, i.e. não há vazio (Phys. iv, 214a16), é único (Caelo i, 8 e 9), não foi gerado nem tem "epílogo" ou término (De Caelo i, 10, 11 e 12). Deste modo contradiz a ideia platónica da criação demiúrgica, as concepções de vazio e multiplicidade de Demócrito ou Leucipo, bem como a versão "cíclica" (criação e destruição) de Heráclito de Éfeso. Segundo Aristóteles, o aether (etim. "em perpétuo movimento"), a famosa quinta essentia da filosofia medieval, ou "o primeiro corpo" (como o estagirita mais frequentemente lhe chama), é o constituinte básico das regiões celestes.

Apolónio de Perga e os Epiciclos

Na descrição dos movimentos planetários, duas enormes dificuldades se verificavam: a variável velocidade e as "paragens" e mudanças de direcção (do movimento directo para o retrógrado e vice-versa). Apolónio de Perga (Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos, 262 a.C.-194 a.C.), que viveu cerca de um século depois de Eudoxus, estudou as secções cónicas e estará ligado à teorização do sistema de epiciclos e deferentes (utiliza-se habitualmente a terminologia medieval, e.g., "deferente", pois Ptolomeu (Κλαύδιος Πτολεμαῖος, translit. Klaúdios Ptolemaios, lat. Claudius Ptolemaeus) não utiliza um termo específico para o "concêntrico que transporta o epiciclo"). Os epiciclos (επίκυκλοι) foram introduzidos para acautelar os aumentos e diminuições aparentes nas velocidades da Lua e dos planetas. Esta teoria constitui uma inovação importante, uma representação geométrica dos fenómenos observados e um sistema mais eficiente (na utilização prática) do que o das esferas de Eudoxus e Aristóteles: "The epicycle theory offered a far simpler and more accurate representation of the variable course of the planets than did the rotating spheres of Eudoxus and Aristotle. Moreover it explained their variable brightness as a result of their varying distances from the earth. These distances could be computed easily from the sizes of the circles." (Pannekoek, A., A History of Astronomy, Interscience Publishers & George Allen and Unwin, 1961, p.133)

O rigor de Hiparco; a Sphaerica; antigas medições da circunferência do globo (Eratóstenes e Posidónio)

Hiparco utilizará métodos precisos na representação dos movimentos do Sol e da Lua e, entre muitas contribuições, descobrirá o fenómeno de Precessão dos Equinócios. Na época helenística, Menelaus (Μενέλαος, c. 70 – 140 d.C.), será decerto autor da Sphaerica, único livro deste matemático que sobreviveu (numa tradução árabe). Tripartido, trata da geometria da esfera e da sua fundamental aplicação às medidas e cálculos astronómicos.

Antes, procurou-se conhecer o tamanho da Terra medindo uma porção do meridiano. Eratóstenes de Cirene (276 a.C.-194 a.C.) calculou a circunferência da a partir de uma proporção (a célebre experiência relacionando a distância entre Alexandria e Συήνη [Siena, actual Assuão] e as sombras projectadas, sabendo, segundo o que se dizia, que ao meio dia no solstício de Verão, a luz do Sol incidia perpendicularmente num poço na localidade situada no sul do Egipto).

Esquematização da experiência de Eratóstenes segundo Baker, R. H., Introduction to Astronomy (3rd ed.), D. Van Nostrand Company, 1947, p.4

As medições de Eratóstenes e Posidónio são descritas numa conhecida passagem do livro sobre os movimentos circulares dos corpos celestes (Kυκλικὴ Θεωρία Mετεώρων, Lat. De motu circulari coporum cealestium (I.10)) atribuido a Cleomedes (Κλεομήδης). Aristóteles também refere "matemáticos" responsáveis por outras medições (De Cael., 298a16), bem como Arquimedes (Aren., I.8). Segundo a narrativa mais corrente, Eratóstenes de Cirene (c.276-194 a.C.) mediu a circunferência da Terra utilizando um método que considera a distância entre duas cidades no mesmo meridiano, e sabia que na localidade mais a sul o Sol culminava no zénite no dia do solstício de Verão. A diferença nas sombras medidas por um gnómon ("ponteiro"), permitiu extrapolar o comprimento do meridiano. Segundo Martianus Capella (De nupt. Phil. et Merc., VI.59), a distância entre as localidades foi medida por bēmatistaí, profissionais que determinavam as distâncias a passo. Estimou o meridiano em 252,000 stadia (39,060 a 40,320 km), com um erro de apenas −2.4% a +0.8% (assumindo o valor do "stadion" entre 155 e 160 metros). Estas medidas não são todavia indiscutíveis ou consensuais.

O assunto, ao contrário da versão simplista geralmente divulgada, faz correr rios de tinta entre os académicos há muito tempo (e decerto ainda vai continuar). No último estudo relevante acerca deste assunto, Christopher A. Matthew (Eratosthenes and the Measurement of the Earth’s Circumference (c. 230 BC), Oxford University Press, 2023, ch.5) refere como o método terá utilizado a sombra do gnómon em Alexandria (sabendo antecipadamente que a localidade a sul se situava praticamente sob o Trópico de Câncer nessa época, em função do factor determinante da obliquidade da eclíptica (cuja inclinação de facto estabelece a latitude dos dois Trópicos, correspondendo à medida da declinação do Sol nos solstícios). Quanto às medições das distâncias, refere antecedentes (citados por Estrabão), com margens de erro que se verifica serem muito pequenas, entre localidades na Pérsia e regiões adjacentes durante as campanhas de Alexandre, das quais também infere a utilização do estádio (στάδιoν) Pan-Helénico de 180 metros), a sistemática medição dos terrenos agrícolas no Egipto e a provável informação existente resultante do trabalho dos bematistai treinados ao serviço dos Ptolomeus (soberanos do Egipto). Havia pois capacidade e uma tradição de medições precisas. Relembra-nos que Eratóstenes trabalhou com rácios, proporções, não com medidas angulares (ao contrário do que se repete na pífia explicação popular do procedimento). A divisão em graus, minutos e segundos ainda não era utilizada na sua época (somente um século depois). Antes da utilização de círculos graduados as medidas eram enunciadas recorrendo a proporções, por exemplo ao arco de um lado de um polígono regular.

Do exame das fontes e de toda a literatura especializada, C. A. Matthew, conclui que Eratóstenes utilizou como argumentos o referido estádio Pan-Helénico de 180 metros (havia seis stadia de diferentes comprimentos devido à antiga fragmentação geográfica e política das cidades-estado gregas; o nome "estádio" deriva da infraestrutura comunitária e desportiva) e uma 'diferença latitudinal' de cerca de 4500 stadia entre Alexandria e Siena. Ou seja, privilegiou a diferença de latitude relativamente à distância concreta no terreno seguindo a margem oeste do Nilo (que todavia já conheceria de investigações pretéritas), até porque as localidades não estão, de facto, precisamente no mesmo meridiano. E isso, segundo C. A. Matthew, não interfere no procedimento estimando correctamente a distância entre os paralelos de ambas as localidades a partir da informação das sombras em ambos os mencionados paralelos. A figura de 5000 stadia atribuida por Cleomedes a Eratóstenes seria afinal uma "correcção" feita por Hiparco (há diversas teorias para este facto: talvez Hiparco tivesse tão somente recorrido a informação na "Geografia" do próprio Eratóstenes acerca da distância medida no terreno, que inclui um desvio assinalável na região de Luxor) e os valores que surgem ulteriormente em autores romanos (e.g., 5,040 stadia, resultando nos 252,000 stadia relatados por Plínio) radicariam em ajustamentos ulteriores seguindo idealizações platónicas de perfeição numérica ou talvez para que o número de stadia fosse facilmente divisível em graus. (Ver timeline dos relatos históricos nas pp.280-81). Em resumo, a tentativa de medição da circunferência da Terra não era nova mas esta, na sua genial e inovadora metodologia obteve, segundo a interpretação de C. A. Matthew, um resultado extremamente preciso (~224,100 stadia) para o diâmetro polar. Existem erros na metodologia (elencadas nas pp. 139-141): as localidades não estáo no mesmo meridiano, a Terra não é uma esfera perfeita, o efeito da refracção da luz, etc. Mas quem pode censurar um sábio que ousou este cálculo circa 230 a.C.?

No séc. I a.C. Posidónio (c. 135-51 a.C.) mediu a circunferência da Terra seguindo um método similar, todavia utilizando estrelas e não o Sol. Terá efectuado medições da estrela Canopus (Alpha Carinae, na posterior designação de Bayer) a partir de Rodes e de Alexandria (que na realidade também não estão exactamente no mesmo meridiano). Pelas elevações da estrela relativamente ao horizonte estimou a diferença de latitude entre ambas as localizações. O resultado habitualmente referido é 240,000 stadia ou (supõe-se) 19,200 km. Demasiado pequeno, como comentado por Estrabão. Há todavia dois valores distintos atribuidos a esta medição, como I. E. Drabkin analisou num paper (Isis, Vol. 34, No. 6, Autumn, 1943). Tudo indica que, estando Canopus rasante no horizonte de Rodes, a refracção da atmosfera tenha tido um efeito decisivo no cálculo. Terá sido uma correcção (errada) da distância entre as localidades que comprometeu a proporcionalidade? Em todo o caso, é este valor mais "curto" que será divulgado pelo influente Ptolomeu. Sendo uma estimativa com grande visibilidade em autores sucessivos, contribui (a par da especulação Clássica acerca da proporção entre as massas da terra e da água, da exagerada dimensão da longitude da Ásia no relato de Marco Polo e da sua consequente interpretação pelo médico, matemático e geógrafo Paolo dal Pozzo Toscanelli) na origem do ulterior equívoco de Cristóvão Colombo que, como se sabe, acreditava num valor da circunferência ainda menor e, partindo na direcção de uma mítica Antilia, rumou a oeste em busca do próspero Cipangu (i.e. Japão) de Marco Polo e das Índias quando, em Outubro de 1492, encontrou por puro acaso um dos arquipélagos de um continente "novo" que mais tarde será chamado "América". Segundo Samuel Eliot Morison (Admiral of the Ocean Sea: A Life of Christopher Columbus, Boston, Little, Brown and Co., 1954 (1942), p.65), Colombo aceitou o cálculo do geógrafo e astrónomo Alfraganus (al-Farghānī, séc. IX), assumindo que as milhas (árabes) usadas por este eram equivalentes às mais pequenas milhas "romanas" (ou "italianas") e chegando assim à conclusão que um grau mediria 45 milhas náuticas (um valor demasiado modesto, aproximadamente 75% do verdadeiro). O globo de Colombo era, deste modo, 25% mais pequeno do que o de Eratóstenes, 10% mais pequeno do que o de Ptolomeu e até mais pequeno do que o do seu próprio "mentor" Toscanelli.

André Thevet (1502-1590), "CLAVDE PTOLOMEE PELVSIEN" (i.e. natural de Pelusium, Pelúsio), gravura, Les vrais portraits et vies des hommes illustres, Paris, 1584, f.87r.
(aqui recolhida de reprodução em "Great Astronomers", Robert S. Ball, London, Isbister and Company, 1895). O instrumento que segura revela um anacronismo, tratando-se de uma balestilha ou Báculo de Jacob (com o seu virote e soalha), somente documentado muito mais tarde por Jacob ibn Tibbon (Prophatius) e Gersónides (Levi ben Gerson, 1288-1344). Apesar de especulações quanto a uma "provável" anterioridade, não há evidências concretas e é somente nos mencionados autores que surgem as primeiras descrições. O instrumento é citado em Português pela primeira vez por André Pires e por João de Lisboa, como "balestilha" ou "balhistinha".

Mais tarde chamado "divino", Ptolomeu (90-168 A.D.), adoptando uma base filosófica predominantemente aristotélica, será um sistematizador e uma referência incontornável em diversas disciplinas por muitos séculos, em particular fundamentando matematicamente os fenómenos astronómicos no seu Μαθηματικὴ Σύνταξις (Mathēmatikḕ Sýntaxis), em 13 livros, e que virá a ser conhecido como Almagesto. O seu sistema tornou-se complexo porque procurou explicar os efeitos provocados pela (então desconhecida e jamais ponderada) configuração elíptica das órbitas planetárias (uma questão que será dilucidada por Kepler muito mais tarde). No paradigma da sua época, nunca lhe ocorreria que todos estes complexos epiciclos e deferentes não fossem afinal mais do que a reprodução da órbita anual do nosso planeta transferida para cada um dos planetas exteriores, nem colocar Mercúrio e Vénus em órbita solar (como parece já ter sido sugerido na Antiguidade). Noutro tratado ponderou e resumiu as influências e juízos astrológicos (Tetrabiblos ou Apotelesmatiká [os "efeitos" ou "influências"]).

O primeiro manuscrito completo que conhecemos do tratado astrológico data somente do séc. XIII. Mas existem excertos mais antigos no manuscrito florentino Laur. gr. 28,34 (L) do séc. XI, cópia de uma antologia de textos astrológicos conhecida como Syntagma Laurentianum (séc. IX), vide Heilen, Ptolemy’s Doctrine of the Terms and Its Reception, p.59 (in: Jones, A., (ed.), Ptolemy in Perspective..., Springer, 2010), [N.B.: O chamado Centilóquio (ar. Kitab al-Tamara (suposta tradução do gr. καρπος), o Livro dos Frutos, "colhidos" nos ensinamentos do Tetrabiblos, constitui um acervo de cem aforismos. Outrora atribuído a Ptolomeu, é considerado apócrifo, tendo um racional diferente do encontrado no texto pretende "sumariar".]

Os árabes conhecerão Ptolomeu como "Batlamyus". O Almagesto é o verdadeiro compêndio, "obra prima da exposição técnica" e a principal referência da astronomia antiga, também valiosa fonte de informação da obra de Hiparco (cujos textos originais se perderam). Tratado matemático e astronómico, "canonizou" o modelo geocêntrico. Expende as teorias dos movimentos do Sol, da Lua e dos planetas, explica a astronomia esférica e as coordenadas relevantes, a paralaxe, os eclipses, a precessão, etc. Também contém um catálogo estelar. É um dos textos científicos mais influentes de todos os tempos, autoridade até o século XVI. Segundo o seu editor G. J. Toomer, somente os Elementos de Euclides revelaram maior longevidade. O seu nome era "Μαθηματικὴ Σύνταξις" (Mathēmatikē Syntaxis). Segundo uma interpretação, tornou-se conhecido pelo título transliterado Hē Megálē Sýntaxis ("A Grande Colecção"). Os árabes passaram a designá-lo pelo superlativo daquele adjetivo (megístē), por corruptela: al-majisṭī, que gerou Almagesto:

This is undoubtedly derived (ultimately) from a Greek form μεγίστη (sc. σύνταξις), meaning ‘greatest [treatise]’, but it is only later that it was incorrectly vocalised as al-majasti, whence are derived the mediaeval Latin ‘almagesti’, ‘almagestum’, the ancestors of the modern title ‘Almagest’. (Toomer, Ptolemy's Almagest, Duckworth Books, 1984, p.2).

O principal canal para a redescoberta deste texto no Ocidente Latino foi a tradução de Gerardo de Cremona, feita a partir do Árabe em Toledo e completada em 1175.

Principais edições modernas
Foi editado sob o título Syntaxis mathematica por J. L. Heiberg em Claudii Ptolemaei opera quae exstant omnia, vols. 1.1 and 1.2 (1898, 1903). Em Inglês, depois da edição de R. Catesby Taliaferro (1952), existe a mais recente e excelente edição de G. J. Toomer (Ptolemy's Almagest, Duckworth Books / Spinger Verlag, 1984, com segunda edição em 1998 e uma revised edition publicada em 1998 pela Princeton University Press). Há também uma tradução parcial por Bruce M. Perry em The Almagest: Introduction to the Mathematics of the Heavens, Green Lion Press, 2014. A tradução alemã de Karl Manitius (1912, 1913) é baseada na edição padrão de Heiberg. Em Francès, foi vertido do Grego por Nicholas Halma (em dois volumes editados em 1813 e 1816).

Ptolomeu, "Le législateur de l'astrologie grecque", segundo Bouché-Leclercq (1899, p.95), utilizando um quadrante, acompanhado pela Musa da Astronomia. Enverga uma coroa régia, vestígio da tradicional (e equívoca) associação à dinastia Lágida (de Lagos, lugar-tenente de Alexandre) ou Ptolomaica, que governou o Egipto Helenístico. Na sua famosa enciclopédia, Isidoro de Sevilha (c. 631 A.D.), designa-o "Ptolemaeus rex Alexandriae" (Lib. Etym. iii, 26). Gravura da Margarita Philosophica de Gregor Reisch, Basileia, 1508 (primeira edição é de 1503)

Depois do prefácio, Ptolomeu elenca seis proposições ou hipóteses físicas na base do seu modelo astronómico:

I. Os céus movem-se circularmente ("esfericamente");
II. A Terra, tomada como um todo, é esférica;
III. A Terra situa-se no centro dos céus, no que diz respeito aos sentidos (à observação);
IV. A Terra tem a dimensão de um ponto relativamente ao tamanho dos céus (i.e. da esfera celeste);
V. A Terra está imóvel, não executa qulquer movimento envolvendo mudança de sítio;
VI. Existem dois movimentos primários diferentes nos céus: (1) o diurno, que "arrasta" tudo de Leste para Oeste sempre da mesma maneira e à mesma velocidade e (2) o movimento dos luminares e dos planetas, seguindo (mais ou menos rigorosamente) a Eclíptica, de Oeste para Leste.

Os historiadores tradicionalmente associam filosoficamente Ptolomeu e Aristóteles sem qualquer dificuldade. Mas pode argumentar-se que Ptolomeu estará em contradição com Aristóteles ao privilegiar filosoficamente a Matemática em detrimento da Teologia: "Ptolemy began the work [Syntaxis] with a philosophically oriented preface, in which he discussed the organization of knowledge, concentrating particularly on the nature of and relationships between physics, mathematics, and theology. Here, in the preface, we see the first indication that Ptolemy broke with Aristotle, for he argued that mathematics is the highest form of philosophy, rather than theology." (Taub, Lisa Chaia, Ptolemy's Universe: The Natural Philosophical and Ethical Foundations of Ptolemy's Astronomy, Chicago, Open Court, 1993, p.3).

As mais relevantes escolas filosóficas da época incluíam a Academia (platónica) e o Peripatos (por Teofrasto, romaniz. Theóphrastos, discípulo dilecto de Aristóteles), ambas datando do séc. IV a.C.; depois a Stoa (a escola estóica, instalada por Zeno de Citium no séc. III a.C.), os Cépticos, os Neo-Pitagóricos e outros que desafiam categorização.

Ptolomeu teve, como Neugebauer referiu de passagem, uma atitude filosoficamente "eclética". A íntima associação filosófica aristotélico-ptolomaica parece, portanto, ser uma perspectiva algo simplificadora. No livro II das suas Hipóteses Planetárias (Ὑποθέσεις τῶν πλανωμένων), que sendo menos "instrumental" do que o Almagesto privilegia questões cosmológicas, Ptolomeu (segundo a interpretação de Lisa Taub), ataca directamente a Física Aristotélica e, mais espantoso, "dilui a distinção entre as duas naturezas" e defende a natureza animada dos planetas, fazendo uma analogia com o vôo das aves. Refere que o mesmo se testemunha noutras obras do alexandrino. (Taub, Op. cit., p.4; 112 et seq.).

Na sua monumental L'Astrologie grecque (1899), Bouché Leclercq (p.576, n.1) vagueou pelo milefólio de atribuições fantasiosas do conhecimento astronómico aos deuses e heróis das lendas clássicas. O nosso resumo é incompleto e remetemos para o original, particularmente para as referências bibliográficas. Os ilustres representantes da Astronomia/Astrologia são imensos e surgem da tendência evemerista de interpretar os mitos numa óptica social e histórica. Nessa perspectiva, Atlas (condenado a suportar os céus, simultameamente Titã e montanha), torna-se um astrónomo, tal como Prometeu, Cefeu e outros (Cícero, Tusculanae Disputat. V. 3. Virgílio, Aen., I, 741. Plin., VII, 203). É filho de Lybia (personificação da África, "Lybiae filius", segundo Plínio, Nat. Hist., I, c; Eusébio, Praeparatio Evang., X). A associação das Colunas de Héracles a Atlas (Heródoto, ap. Clemente, Stromata ("Miscelânea"), I, 15) transformará (especula Leclercq) o herói musculado em aluno do gigante mitológico. Para os que seguiam Heródoto (Hist. II. 2), segundo o qual os Egípcios acreditavam que os Frígios eram a nação mais antiga, Atlas seria oriundo dessa nação. Os Cários (nas costas agrestes da Ásia Menor) e os Fenícios também concorriam para o título de nação disseminadora do conhecimento astronómico. Prometeu, que deu ao Homem o Fogo do Conhecimento, também seria astrónomo e teria o seu observatório no Cáucaso! Foi, talvez pela proximidade geográfica, hic primus astrologiam Assyriis indicavit ("o primeiro a ensiná-la aos Assírios" (aqui representando os povos da Mesopotâmia), segundo Servius, Eclog. VI, 42). Quíron, preceptor de Aquiles, e sua filha Hipe, também entram no rol dos sábios e astrónomos. O sábio Centauro também teria ensinado Medicina a Asclepius e Astronomia a Herácles. E a lira heptacorde de Orfeu também podia simbolizar os planetas (Ps-Luciano, Astrol., 10). Tirésias, o profeta da Odisseia, "descobre" o sexo dos planetas. Atreu, Belerofonte, Dédalo, Ícaro, Endimião et al. também são astrónomos. A Pítia de Delfos representava Virgo, o Apolo de Dídimos é um dos Gémeos (Gemini), o Oráculo de Ámon em Siwa (visitado por Alexandre Magno) estaria relacionado com Aries, o adultério de Marte e Vénus (Ares e Afrodite) na Ilíada era a conjunção dos planetas correspondentes, etc. Também há o sincretismo com os deuses estrangeiros, sendo Hermes-Thot exemplo paradigmático, autor de "milhares de livros". Deuses e sábios do Egipto e Caldeia são por demais referidos (e.g., Nechepso e Petosíris). A Ishtar babilónica passa a ser a instrutora de Hermes (Hygin., Astron., II, 42) e o Bel mesopotâmico (na realidade um título de diversas divindades) é o inventor das disciplinae sideralis (Martianus Cap., VI, 701). Segundo o épico Nono (Nonnus) de Panópolis, o Herácles Tírio (i.e. de Tiro, na Fenícia) é chamado Sol, Deus Universal, etc. E Leclercq acrecenta: "Cet Hercule fait un cours d'histoire à Bacchus et lui fait cadeau de sa robe constellée, le vêtement légendaire des astrologues". Noutro contexto, será o Patriarca Abraão a transportar a Ciência da sua Caldeia natal para o Egipto, tendo os Fenícios levado para a Beócia o que aprenderam com os Hebreus. E as curiosas referências continuam.

Como o académico Checo Daniel Špelda refere (The Search for Antediluvian Astronomy: Sixteenth- and Seventeeth-Century Astronomers’ Conceptions of the Origin of the Science (Journal for the History of Astronomy, vol.44. Issue 3, August 2013), na Renascença, um período fascinado com as origens da História e das instituições culturais, acreditava-se na existência de um legado transmitido por Deus no "Início dos Tempos", e era a essa tradição perene que se deveria resgatar. Mais tarde, nos séculos XVI e XVII, acreditava-se que a Astronomia (enquanto saber prestigioso e de amplo alcance simbólico) teria existido na Mens Divina como um "Plano Eterno", de acordo com o qual os corpos celestes foram criados e os seus períodos e revoluções definidos. As ideias acerca da origem num passado áureo respaldavam-se em autores clássicos, com a habitual referência ao Antigo Egipto enquanto fonte dos saberes matemáticos (Heródoto, Historiae II, 50; II, 82; II, 143; Platão, Timaeus 22b; Plutarco, De Iside et Osiride X, 35E; Plutarco, De animae procratione in Timaeo 33, 103A–B; Diógenes Laertius, Vitae philosophorum, Proemium, VIII, 2–3; III, 6; Diodoro da Sicília (Siculus), Bibliotheca historica I, 69, 3–4;). Todavia, pelo menos desde a época Helenística, historiadores Judaicos contestaram essa versão e apresentaram a alternativa "adâmica" da origem desses saberes. Destaca-se a apologia de Flávio Josefo (Yosef ben Mattityahu) nas suas Antiquitates judaicae. Aí, fala-nos de Adão e dos seus descendentes (I, 2, 68–71; Jewish antiquities I–IV, H. St. J. Thackeray (trans.), 1961, 32) e encontramos a célebre referência a Seth, que antes do Dilúvio gravou em dois pilares, um de tijolo e outro de pedra, o conhecimentos que deveria sobreviver e ser transmitido à Humanidade futura. E teria sido o Patriarca Abraão, vindo de Ur na Caldeia, a ensinar os Egípcios que depois transmitiram aos Gregos os fundamentos da Aritmética e da Astronomia (Antiquitates judaicae I, 167–8, Jewish antiquities, 82.). Josefo terá uma recepção muito favorável por parte dos académicos Cristãos do início do período moderno. A provecta idade dos antigos patriarcas entrava na argumentação como uma vantagem na aquisição do conhecimento dos ciclos e períodos astronómicos. Neste ambiente cultural, não admira que também a astronomia tenha já surgido na segunda metade do séc. XV nas contrafacções de um impostor como o dominicano Annius de Viterbo (nascido Giovanni Nanni), no Berossi sacerdotis Chaldaici Antiquitatum libri quinque, onde falsifica uma obra que atribui ao respeitado Beroso (ou Berossus, séc. III a.C.). [Para além de criar genealogias e "registos" do passado baseado em "obras perdidas" que afirmava ter "reencontrado" em Mântua, e que influenciarão equivocamente, por exemplo, a nossa historiografia penínsular até finais do séc. XVIII.]. Entretanto, com os resumos que chegavam da China pela pluma dos Jesuítas, começamos a observar o conflito da cronologia bíblica com a presumida antiguidade das efemérides e registos orientais. Hevelius acreditava que os chineses já usavam efemérides antes do Dilúvio Universal mas, em conformidade com a doutrina, considera que, "sem dúvida", aprenderam Astronomia com os Antigos Patriarcas (Machina coelestis, Danzig, 1673, 17): “Scientiam Sideream ab Asiaticis, praesertim Chinensibus primam suam duxisse originem; sine dubio ne a se ipsis, sed a Noa, vel Primis Patriarchis eam hauserunt.”).

Todavia, desde Gassendi, Cellarius e Cassini que se procura racionalizar (e depois rejeitar) a interpretação exposta. Segundo Giovanni Domenico Cassini: “Les grands Ouvrages n’étant jamais parfait dès leurs commencement. (...) Ainsi l’Astronomie & la Géographie se perfectionoient peu á peu." (De l’origine et du progrès de l’astronomie (1693), in: "Mémoirs de l’Academie Royale des Sciences: Depuis 1666 jusquà 1699, viii: Oeuvres diverses de M. I. D. Cassini" (Paris, 1730), 1–54. 18f.). Lenta e gradualmente, como Špelda salienta, a perspectiva "retrógrada" e embebida na Teologia de uma prisca sapientia será substituída pela abordagem "progressista" que acredita no incremento do conhecimento a partir de rudimentares alicerces e não na "recuperação" de um conhecimento divino de uma qualquer "idade edénica". Todavia, em finais do séc. XVIII, Jean Sylvain Bailly (Histoire de l'Astronomie Ancienne) ainda acreditava que os conhecimentos astronómicos das "raças civilizadas" da antiguidade eram apenas "destroços" de uma astronomia "perfeita" que existiu em tempos ante-diluvianos:

"Quand on considere avec attention l'état de l'Astronomie dans la Chaldée, dans l'Inde & à la Chine, ON Y TROUVE PLUTÔT LES DÉBRIS QUE LES ÉLÉMENS D'UNE SCIENCE; ce sont des méthodes asséz exactes pour le calcul des éclipses qui ne font que des pratiques aveugles, sans nulle idée des principes de ces méthodes, ni des causes des phénomènes;" (Livre Prémier, ch. XII [maiúsculas no original])

E como se conservou esse saber ancestral? Bailly escreve:
"Si l'on nous demande comment ces connoissances se sont conservées & ont été transmises à la postérité, nous répondrons que les colonnes chargées de caractères hiérogliphiques, sont les dépots qui ont survécu au déluge. Ces monumens des antiques habitans de la terre, étoient sans doute très-nombreux dans l'Asie." (ibid., cap. XIII)

Para além da perspectiva difusionista (v. em particular o Liv. III) e evemerista (referindo esses "homens notáveis" de um passado remoto que foram, e.g., Uranos, Atlas, Chiron, Thot, Belus [Bel]) e surpreendendo-nos com afirmações tais como: "On avoir donné aux planètes le nom des premiers hommes célèbres." (Liv. IV, cap. IV), Bailly menciona os Atlantes de Platão (Liv. I, caps. IV-V) que assimila aos de Diodoro Sículo, considerando estes últimos povos africanos os antepassados dos Egípcios e dos Etíopes (Liv. IV, cap. I). Um precursor de Ignatius Donnelly.

Estuda-se hoje com revigorado interesse o intercâmbio de influências, as inovações e diversificadas materializações locais. As peripécias da transmissão do conhecimento e o percurso das traduções de suporte é interessantíssimo e surpreendente.

Intercâmbios culturais, com particular enfoque na Ásia (Michio Yano, in Micrologus, XXVI, 2016; pp.457-74)

O sincretismo da época helenística recolherá muitos dos contributos referidos: gregos, mesopotâmicos, egípcios, persas, indianos... é o período fundamental. Otto Neugebauer, na perspectiva da ulterior concepção europeia do progresso da ciência, afirmou taxativamente: "Up to Newton all astronomy consists in modifications, however ingenious, of Hellenistic astronomy." (The Exact Sciences in Antiquity, (2nd edition), Dover Publications, 1969, p.4). É verdade, na perspectiva dos futuros desenvolvimentos científicos. Somente muito mais tarde, Newton e os seus contemporâneo introduzirão a Dinâmica na discussão dos fenómenos astronómicos. Mas tende-se hoje a investigar e valorizar os insuspeitados intercâmbios entre diferentes tradições.

Na Índia, um sistema de "marcadores" siderais configurava uma lista de nakshatras (análogas às "mansões lunares", manazil al-qamar, dos árabes), com utilização calendárica e astrológica. O "caminho da Lua" era balizado por determinados asterismos.

Os Nakshatras constituem o alicerce da tradição indígena da Índia, recuando a um contexto ritualístico antigo de determinação do tempo específico para executar determinados rituais ou práticas espirituais. São referidos pelos nomes convencionais no Atharvaveda (Livro 19, Hino VII), que data provavelmente de 700-800 a.C. (um pouco mais antigo segundo Gavin Flood; datado c. 1200-1000 segundo Michael Witzel). Na tradição da Índia, a astrologia que "elege" um momento auspicioso sempre se baseou nos Nakshatras, i.e. nas constelações reais, siderais, do percurso da Lua, e ainda hoje o Zodíaco é preterido, podendo nem ser utilizado. A tradição astrológica Indiana (Jyotisha) mais antiga era, acima de tudo, calendárica. As técnicas especificamente horoscópicas surgem mais tarde no contacto com a tradição Helenística. De acordo com o académico Asko Parpola, a tradição Jyotisha e as descobertas relacionadas com o calendário luni-solar da Índia Antiga (bem como descobertas similares na Antiga China) são, muito provavelmente, paralelas e não oriundas de uma difusão comum a partir da Mesopotâmia, como se supunha: "...from convergent parallel development, and not from diffusion from Mesopotamia" (Beginnings of Indian Astronomy, with Reference to a Parallel Development in China, in "History of Science in South Asia", Vol. 1, 2013, pp.21–25). Mais tarde assiste-se à fusão com elementos Helenísticos (e depois Arabo-Persas) importados que serão "indianizados" e "sanscritizados", dando origem à horoscopia praticada no subcontinente.

Na cosmologia dos Puranas (literatura popular de carácter enciclopédico, com datação variável e muito debatida, sendo seguro afirmar que foram registados, a partir de tradições orais pretéritas, ao longo do primeiro milénio da nossa era), uma série de rodas carregam os céus em torno da Terra. Os seus eixos estão fixados no monte sagrado (Meru), a sua força motriz é a "respiração de Brahma". Uma visão híbrida influenciada pela cosmologia grega mas não agilizada em termos de geometria esférica.

Segundo P. Whitfield (The Mapping of the Heavens, Pomegranate Artbooks, 1995, p.20), a sabedoria hindu foca-se, acima de tudo, nos caminhos para escapar ao mecanismo do destino e ao ciclo da acção e do sofrimento, e aqui a Astrologia assumiu um papel central.

Segundo Montelle (Op. cit., p.168), a astronomia indiana é acima de tudo "utilitária": «...emphasis was primarily on the instruction of individuals who functioned in society for consultation regarding the correct times for the numerous religious requirements, the management of the various facets of astrological practices, the organization of the calendar, and related tasks. Efforts on the part of these professionals were primarily directed toward practical considerations and astronomy therefore remained essentially a practical endeavor. For the most part, this attitude was collectively sustained, to the detriment of deeper theoretical inquiry and organization». Os intercâmbios com outras culturas foram sistemáticos, mas as incorporações eram sempre adaptadas e contextualizadas: «However, these external influences were evaluated and incorporated for the ways in which they corroborated and ratified the divinely revealed indigenous content, and not for the inspiration they might provide to consider things in another way. For these reasons, Indian astronomy is reasonably characterized as "the recipient and remodeler of foreign elements."» (ibid.)

Astrónomos Indianos - BL Ms Ori5259 f.29

Astrónomos Indianos determinando coordenadas (do Sarvasiddhãntatattvacudamanii, composto por Durgãsankara Pãthaka, anos de 1830; British Library, Ms Or.5259, f.29)

Por seu lado, a tradição persa está principalmente associada à utilização de orbes planetários, às relações astrológicas entre os seus movimentos recíprocos e, particularmente, aos grandes ciclos cronológicos, em particular os que se baseiam nas conjunções dos planetas mais ponderosos, Júpiter e Saturno. David Pingree fez recuar a origem das modalidades de "astrologia histórica" (baseada nas conjunções de Júpiter e Saturno nas diferentes Triplicidades elementares) justamente à Pérsia Sassânida, período entre os séculos II e VI [From Astral Omens to Astrology, 1997, pp.49 e 64]).

Em contraste com a abordagem planetária e eclíptica que se encontra noutras geografias, Joseph Needham salientou o proeminente carácter polar e equatorial da astronomia da China:

"I think one could really say that the celestial pole was the fundamental basis of Chinese astronomy. It was connected also with the microcosmic—macrocosmic type of thinking, because the pole corresponded to the emperor on earth, around whom the vast system of the bureaucratic agrarian state revolved naturally and spontaneously. I mentioned the gnomon (piao) just now, and clearly the meridian concept would arise very easily from this upright stick, because if you looked south you could measure the noon shadow, and if you looked north during the night you could measure the times at which the various circumpolars made their upper and lower transits. We have this in so many words in Chinese texts. Moreover, just as the influence of the Son of Heaven on earth radiated in all directions, so the hour-circles radiated from the pole. During the — 1st millennium the Chinese built up a complete system of equatorial divisions defined by the points at which the hour-circles transected the equator (the chhih tao); and these divisions contained the 28 ‘lunar mansions’ (hsiw), like segments of an orange filling up the celestial sphere, bounded by hour-circles and named from the constellations providing the ‘determinative stars’ or boundary markers (chii hsing)." ("Astronomy in ancient and medieval China", in: F. R. Hodson (ed.), The Place of Astronomy in the Ancient World, Op. cit., 1974, pp.68-69)

Na China Antiga o mundo habitado era chamado "tianxia". Não havia uma "astronomia" enquanto disciplina específica ou autónoma. Por um lado, havia o estudo dos métodos calendáricos ("lifa"), cuidando das regularidades. Por outro, e de algum modo relacionado, existiam os padrões dos fenómenos celestes ("tianwen"), atentando-se nos que assumiam carácter imprevisto ou episódico e interpretando-os sempre na perspectiva do mundo, da sociedade e do Estado. (Hoskin, M. (ed.), The Cambridge Illustrated History of Astronomy, Cambridge University Press, 1997, p.48). Os métodos matemáticos, embora gradualmente mais sofisticados, eram somente aritméticos e não geométricos, não colocando qualquer ênfase na interpretação do espaço tridimensional. Exploravam ciclos de longo prazo.

A medição do tempo é essencial em qualquer cultura. Reconstituição da torre do relógio astronómico de Su Song em Kaifeng (c. 1090 AD). O seu ritmo regular era conseguido pela água corrente que enchia ciclicamente pequenos vasilhames numa roda. Os chineses compreenderam as variações a que a água estava sujeita dependendo da temperatura (os extremos são a evaporação e o congelamento), e passaram por vezes a utilizar mercúrio nos relógios mais precisos. (desenho de John Christiansen, in: Needham, J., Science and Civilization in China, vol. IV, pt 2, 1965, fig.650)

Segundo A. Pannekoek, "Chinese philosophy sought to find symmetry and relationship in life and world. The four directions, east, south, west and north are correlated with the four seasons, the four parts of the day, the four sections of the celestial equator. Added to the ‘middle’, they constitute a pentad correlated with other pentads in different realms; elements or basic matters, plants, colours, parts of the body, musical instruments, planets, flavours. Combined with another series of twelve differing kinds, it produces a period of 60 years for use in chronology. There is a kind of arid harmony of schematic order in this world doctrine with its associated rites." (Op. cit., p.88). "Chinese astronomy was a government service." (Thurston, H., Early Astronomy, Springer-Verlag, 1994, p.84). No Império do Meio, assistiu-se à divisão dos céus seguindo esquemas que privilegiavam as perenes estrelas circumpolares. Um dos mais antigos foi o dos "Cinco Palácios". Depois da região circumpolar havia: o Palácio do Leste (simbolizado pelo Dragão Azul), o Palácio do Sul (simbolizado pelo Pássaro Vermelho), o Palácio do Oeste (simbolizado pelo Tigre Branco) e o Palácio do Norte (simbolizado pelo Guerreiro Negro coadjuvado pela tartaruga e pela serpente). Outro esquema recorria a nove divisões. a circumpolar e oito atribuídas a cada um dos hexagramas do I Ching (ou Yi Jing), Livro das Mutações. Ainda outro, bem diferente, era baseado nas "estações" de Júpiter (quando o planeta "pára" e alterna entre o movimento directo e o retrógrado). Utilizava o ciclo de doze anos da órbita do planeta, dividindo o Equador (e, por extensão, a Eclíptica) em doze sectores (em nada relacionados com a divisão zodiacal que conhecemos), recorrendo a um "planeta-sombra" fictício (tai sui) que imitava o movimento de Júpiter na direcção inversa (vide Ronan, C., Astronomy in China, Korea and Japan, in Walker, C. (ed.), Astronomy Before the Telescope, BCA, 1996, em especial pp.253-64). As considerações cosmológicas chinesas (que se nutriam de um aparatoso simbolismo) parecem ter coabitado com a vertente operativa da astronomia e do calendário de modo pacífico. A ideia da esfericidade, quando equacionada, não se imiscuía na astronomia ou na geografia. As representações do mundo continuavam a ser convencionais, considerando-o plano. Seguindo um resumo de Hugh Thurston (Op. cit., pp.90-1), no que diz respeito às teorias especulativas sobre a estrutura do Universo, a primeira a ganhar coerência terá sido a Gaitan ("cobertura celeste"), na qual a a terra e o céu eram partes de duas esferas, todavia mantendo a concepção ["inexplicable", segundo Thurston] de um mundo terreno "quadrado" ou quadripartido. Uma segunda teoria, Huntian ("Esfera Celeste"), recua pelo menos a 100 a.C. Era seguida no final da disnastia Han e fazia equivaler os céus a um ovo, tendo a Terra como a gema. Metade do céu estava repleto de água, outra metade de vapor. O mundo habitado flutuava na água. Noutra cosmovisão, Xuanye ou "Escuridão Omnipresente", o Sol, a Lua e as estrelas são compostos de vapor condensado e flutuam livremente no espaço.

Wakan Sansai Zue - constelações circumpolares

Constelações circumpolares chinesas, de uma edição de 1901 do Wakan Sansai Zue, enciclopédia ilustrada escrita no Japão por Terashima Ryoan em 1712.
As duas cadeias quase verticais de estrelas delimitam o "Palácio Púrpura Interdito". O asterismo principal da nossa Ursa Major surge desenhado à direita neste mapa.

Os chineses raramente se referiam em termos de um "deus" para além do mundo, responsável pela criação. Os céus eram a instância suprema e o Imperador o seu filho, a cabeça do Estado e da sua religião. Os augúrios eram observados e relacionados com regiões, cidades ou até com divisões do Palácio Real. O mais importante ritual relacionado com o céu acontecia no solstício de Inverno, quando o Yang voltava a aumentar após ter atingido o meu momento mínimo. (North, J. D., The Norton History of Astronomy and Cosmology, W. W. Norton & Company, 1994, pp.137-9).

Apesar das melhores práticas que abordaremos de seguida, conhecer a hora certa era no passado tarefa difícil. Séneca revelava satiricamente quão complicado era saber horas exactas pois seria "...mais fácil os filósofos estarem de acordo entre si do que os relógios." (Apocolocyntosis divi Claudii, ii. 2-3). Todavia, os gregos aplicaram aos mecanismos de medição do tempo as projecções gnomónica e estereográfica e por vezes recorreram a complexos sistemas de rodas dentadas.

[Segue-se resumo traduzido a partir de exposição de Robert Hannah: Oxford Classical Dictionary (em linha: https://doi.org/10.1093/acrefore/9780199381135.013.1683)]

Para conhecer a "hora" aproximada durante o dia bastaria, de modo imediato, medir com os pés a própria sombra projectada. O método expedito já é mencionado pelo dramaturgo Aristófanes (na comédia Ecclesiazusae, 651–652). A primeira utilização documentada do gnómon (em rigor, o estilo, a parte do relógio solar que possibilita a projecção da sombra) pelos gregos está associada a Anaximandro (séc. VI a.C.). A fonte é o biógrafo e doxógrafo Diógenes Laércio (Laértios), que contudo nos informa que se destinava a conhecer o tempo no calendário e não no dia (Diog. Laert. 2.1). Deste modo, parece aqui associá-lo a uma utilização calendárica. Sabemos, todavia, como constitui o instrumento "primevo" da abordagem à estimativa do momento do percurso do Sol durante o dia. Entretanto, Heródoto refere que o conhecimento do gnómon, na utilização convencional como "relógio", teria origem na Babilónia (Hist. 2.109.3), atribuíndo a mesma origem ao conhecimento das "duodécimas partes do dia".

Segundo Robert e Margaret Mayall, um passo fundamental terá sido a descoberta da vantagem em alinhar o gnómon com o pólo celeste, ajustando-o à latitude específica do local. (Mayall, R. Newton and Mayall, Margaret W., Sundials: How to Know, Use, and Make Them (2nd edition), Sky Publishing Corp., 1973, figure 7)

Havia dois tipos de 'horas': sazonais e equinociais. Na astronomia preferiu-se a utilização das horas equinociais (assim designadas porque eram iguais às horas sazonais nos dias dos equinócios; são as horas iguais que hoje utilizamos). As primeiras possuem tamanho variável consoante as estações do ano. Os mais antigos relógios de Sol que sobrevivem da cultura grega são fragmentos de dois exemplares planos, um proveniente de Olímpia e outro do Amphiareion, um santuário em Oropos na Ática. Este tipo plano encontra-se na horizontal ou na vertical, mas também inclinado equatorialmente (em função da latitude do lugar), como o exemplar de Oropos.Sendo o mais fácil de construir, torna-se o mais difícil de desenhar (i.e. as marcações) pois o hemisfério do céu precisa ser projectado num plano. Ambos os referidos relógios são, basicamente, blocos de mármore planos com incisões de linhas horárias irradiando, numa configuração de "ventoínha", a partir do ponto "axial" do gnómon, demarcando os limites das doze horas diurnas. Assemelham-se aos (mais antigos) modelos verticais egípcios, que podem aqui ter tido uma influência directa. Todavia, ao contrário desses, os dois modelos gregos mostram horas equinociais (iguais) e não sazonais. O exemplar de Oropos acrescenta linhas de data para assinalar os equinócios e os solstícios.

Um dos tipos mais comuns de relógio era esférico: uma cavidade hemisférica removida de um bloco de pedra com um ponteiro no centro. Eram inscritos os círculos fundamentais (Equador, Trópicos e, obviamente, as linhas das horas) (James Evans, Material Culture of Greek and Roman Astronomy, in: C.L.N. Ruggles (ed.), "Handbook of Archaeoastronomy...", Op. cit., vol.3, ch. 141, p.1590).

Relógio solar plano e vertical mais tardio, Bizantino, século IX-X. As horas são numeradas, à maneira grega, com letras do alfabeto. (Museu Arqueológico de Istambul, inv. no. 905T. Crédito: R. Hannah). O sistema grego de numerais utilizava as 27 letras do alfabeto; as primeiras nove para as unidades de 1 a 9, as seguntes para as dezenas a partir de 10, as restantes para as centenas, etc. Estes numerais podiam ser utilizados para escrever números mas eram extremamente inadequados para as operações, e.g., adicionar, subtrair, multiplicar, dividir (principalmente números grandes)

O outro sistema principal de mecanismo de medição do tempo era o relógio de água. Na Grécia, o seu nome era κλεψύδρα‎ (clepsidra: “que rouba água”). Mecanismo referido no De Caelo de Aristóteles (294b.14–30) e em muitas outras fontes. A clepsidra era de tal modo usada que, por volta do IV século a.C., o orador Demóstenes podia utilizar a palavra "água" (ὕδωρ‎) como sinónimo de "tempo" (Dem. Poly. 2; De cor. 139; De fal. leg. 57). Uma abordagem alternativa seria relacionar explicitamente a passagem do tempo com as estrelas, através do relógio a que o romano Vitrúvio chamou "anafórico" (De arch. 9.8.8–15) O termo deriva do Grego ἀναφορά (anaphora), significando o "nascimento", o elevar de uma estrela. Era um mecanismo automático que permitia conhecer a hora a partir de uma representação da sequência das constelações que se elevavam durante o dia (numa espécie de mostrador). O mecanismo, variante da clepsidra, seria alimentado por uma corrente de água constante. Entretanto, uma interessante estrutura é a chamada "Torre dos Ventos", em Atenas. Também é conhecida como Hōrológion ou Horologium em Latim, datando provavelmente do séc. I a.C.. Pelos vestígios arqueológicos, decerto integrava um sistema de relógio de água, para além de marcações das horas nas suas oito faces. Por esta altura havia diferentes tipos de relógios de Sol (Vitrúvio, De arch. 9.8.1, refere catorze, dos planos aos esféricos, cilíndricos, cónicos, etc., atribuíndo-os a diversas autoridades, a começar em Eudoxo).

Um último instrumento, peculiar, é o prodigioso "Mecanismo de Antikythera" (Anticítera), resgatado no Mar Egeu por pescadores de esponjas por volta de 1900 (vide Derek Price: Gears from the Greeks: The Antikythera mechanism, a calendar computer from ca. 80 B.C. Transactions of the American Philosophical Society 64. Philadelphia: American Philosophical Society, 1974). Tecnologia de ponta, decerto muito raro, combinava uma diversidade de modalidades de contagem do tempo. Muito mais tarde submetido a raio X e TC, sabemos que utilizava cerca de trinta rodas dentadas (num sistema diferencial que se julgava ter sido somente descoberto pouco antes da Renascença). Correlacionava os ciclos do Sol e da Lua, o chamado "Ciclo Metónico" de 19 anos trópicos ou 235 lunações, que permitia relacionar os calendários solar e lunar e saber quando uma determinada fase da Lua aconteceria na mesma data do calendário solar. É também provável que traduzisse os movimentos dos cinco planetas conhecidos nos seus movimento epicíclicos através do Zodíaco. Segundo Cícero, Posidonius (c. 135-51 a.C.) também construiu um "modelo do Universo" que exibia os movimentos diurnos dos luminares e dos cinco planetas. (De Natura Deorum, ii-34).

Sistema de rodas dentadas no "Mecanismo de Antikythera" (reconstrução originalmente feita por Derek J. de Solla Price, 1974)

Numa referência aos instrumentos pré-telescópicos (i.e. até ao séc. XVII), podemos incluir, para além do eterno gnómon (ponteiro) dos já mencionados relógios de sol e das clepsidras, o astrolábio (contudo, o astrolábio plano medieval não era um instrumento suficientemente preciso para as medições astronómicas especializadas), o quadrante (preferencialmente de grandes dimensões), mormente fixado numa parede no plano do meridiano e a esfera armilar, que permitia a determinação directa das coordenadas equatoriais e eclípticas. Já o astrolábio esférico (ou esfera armilar) era uma tradução tridimensional da esfera celeste, reduzida aos seus maiores círculos de referência e equipado com um sistema de visada; os círculos de referência eram graduados. Este seria o instrumento "perfeito" e um "modelo do Universo", multifuncional, todavia mais difícil de utilizar e provavelmente preterido relativamente a outros mais simples e especializados (quadrantes, instrumentos para medições zenitais, outros para aferir o momento do equinócio, etc.) com apenas uma funcionalidade.

Os gregos Aristilus e Timocharis estão entre os primeiros astrónomos que determinaram as posições das estrelas de modo (relativamente) preciso, utilizando coordenadas. Por essa altura, Euclides havia expendido a “doutrina das esferas”, i.e. o sistema de coordenadas usado para determinar as posições dos eixos e planos fundamentais aos quais os sistemas de coordenadas dos corpos celestes se referem (Abetti, G., History of Astronomy (Betty Burr Abetti, trans.), Abelard-Schuman, 1952, p.38). No final do séc. XIII assistimos ao aparecimento do 'novo quadrante' (combinação de quadrante e astrolábio) por Don Profeit Tibbon (conhecido como Profatius) e ao chamado "bastão de Jacob" (baculus Iacobi) ou balestilha por outro Judeu Provençal: Levi ben Gerson (conhecido como "Gersónides", 1288-1344). Este instrumento era composto por um virote e uma soalha, que corria na perpendicular em relação ao virote e permitia medir o ângulo entre dois objectos no céu.

Segundo Robert Recorde, todos os instrumentos (de medição angular, subentende-se no contexto) se baseiam, de uma ou outra maneira, na representação da "esfera material": "...yet all these are but parts (at the most) diuers representations of the Sphere" (The Castle of Knowledge, 1556, 2nd Treatise). Como Jean-Pierre Verdet salienta, ao longo dos cerca de dois mil anos que separam Hiparco de Tycho Brahe, os instrumentos de observação 'profissionais', de poste fixo, serão praticamente sempre os mesmos, bem como as respectivas técnicas de construção, materiais e precisão: "D’Hipparque à Tycho Brahe, soit donc pendant près de deux mille ans, le matériel d’observation sera extrêmement réduit et restera pratiquement le même, comme resteront les mêmes les techniques de construction de ces instruments, leurs dimensions (à peu près la taille humaine) et leurs performances. Tous réalisés en bois, les instruments d’observation utilisés, disons à poste fixe, sont au nombre de trois : le quadrant statique, le triquetrum et la sphère armillaire, appelée également astrolabe sphérique, terme que nous éliminerons pour éviter la confusion avec l’astrolabe planisphérique du Moyen Age qui n’a jamais été un véritable instrument d’observation, si ce n’est pour la détermination approximative de l’heure, mais plutôt un instrument à usage pédagogique." (Une Histoire de l'Astronomie, Éditions du Seuil, 1990).

A atitude relativamente aos fenómenos naturais ao longo da Antiguidade não era marcada pela 'causalidade' mas sim pela 'finalidade'. A ligação entre os fenómenos não era vista em termos de 'causa-efeito' mas sim enquanto 'sinal' e 'significado'. (Pannekoek, A., A History of Astronomy, Interscience Publishers & George Allen and Unwin, 1961; trad. nossa)

Os nossos ancestrais mitificavam e interpretaram o Universo seguindo referências familiares do quotidiano, das actividades sociais, cultuais e agrícolas, numa lógica de analogia e no quadro conceptual específico dessa sociedade. Os nomes dos meses hebraicos, e.g., Nisan (“Sacrifício”) ou Airu (“Florescimento”), reflectem a vida ritual e agrária desse povo no "carrossel" que é o ano. Há temas perenes, emergindo em todas as culturas devido à sua importância universal: a ordem, o ciclo da vida e a renovação, a criação, a transcendência, a oposição masculino-feminino, a complementaridade entre forças polarizadas (Krupp E. C., Beyond the Blue Horizon, Oxford University Press, 1992 (1991), p.1 et seq.). Segundo Anthony Aveni, o importante a reter é que estamos perante cosmovisões racionais, em contexto ou "em situação", estruturadas na articulação entre as partes, hierarquia e alternância, relação espírito-matéria e procura de "significado" (Conversing with the Planets, Kodansha America, Inc. 1994, p.177).

Os planetas estão desde cedo ligados ao conceito de “influência” ou “influxo”. Para os antigos, não eram movidos pela gravitação mas pelo seu arbítrio. Tal como as pessoas, tinham uma “alma”. Na Idade Média, por exemplo, toda a natureza estava impregnada pelo Pneuma [conceito estóico recebido dos clássicos], um fluído elástico e invisível que tudo permeava, atribuíndo ao Todo do Universo essa qualidade “animada”. Literalmente significava “Respiração do Universo” (Aveni, Op cit., 154). Era o medium privilegiado e necessário para preencher o vácuo. "[O Éter] é tão essencial como o ar que respiramos”, insistia o físico J. J. Thomson (que descobriu o electrão) em 1909. A Física ainda o procurava (na verdade vários tipos de éter: eléctrico, magnético, etc.) no limiar do séc. XX, apesar de já não considerar a vertente “divina” que antes o enformava (Schaffner, Kenneth F., Nineteenth-Century Aether Theories, Oxford: Pergamon Press, 1972).

Símbolos dos planetas num manuscrito do séc. XV (British Library MS Sloane 428): Saturno, Júpiter, Marte, Sol; Vénus, Mercúrio, Lua e Caput Draconis (nodo lunar ascendente)

Acerca da iconografia, James H. Holden explica: "Neugebauer & Van Hoesen, op. cit. [i.e. "Greek Horoscopes"], pp. 19 & 163, point out that the symbols by which the planets and signs are represented today first appear in medieval MSS. And it might be added that the manuscript symbols differed somewhat from their modem forms, which were regularized by the 15th century printers. The manuscript symbols of the signs were pictorial, while the symbols for the planets were simply modifications of the Greek letters of the planets’ names, e.g. Κ for Saturn (Kronos), Z for Jupiter (Zeus), Φ for Venus (Aphrodite), etc. They were adopted merely for convenience and had none of the “esoteric’ meaning that some modem astrologers have attributed to them." (A History of Horoscopic Astrology, Tempe: American Federation of Astrologers, Inc., 1996, p.14, n.15)

Habitava-se um mundo pleno de correspondências e assinaturas simbólicas, caracterizado pela "cosmisação" do espaço e pela sacralização do tempo (vide Eliade, M., O Sagrado e o Profano: A Essência das Religiões, Livros do Brasil, 1975; 1959; caps. I e II). O calendário e as estações do ano serão determinantes na atribuição da natureza elementar e das qualidades de cada imagem ou signo. Prevalecia um princípio de analogia entre o Todo e as partes, materializado, por exemplo, na teoria elementar e humoral. A filosofia codifica o conceito de “Alma do Mundo” (lat. Anima Mundi) que permeia o Universo. No Timeu (Timaios, o único texto platónico de grande fôlego disponível durante séculos no Ocidente latino através da tradução parcial e extenso comentário de Calcidius), é não somente a Causa Primeira e o Princípio da Vida (Kósmos enquanto ser vivo/organismo vivo) como se lhe atribui cognição (Helmig, Christoph (ed.), World Soul – Anima Mundi: On the Origins and Fortunes of a Fundamental Idea, De Gruyter, 2020. 2.: Plato's Timaeus as a likely 'story'). E neste diálogo platónico, cada "alma" voltará para a "sua estrela" Daí os versos de Dante, no Paradiso (Canto IV):

Ancor di dubitar ti dà cagione
parer tornarsi l’anime a le stelle,
secondo la sentenza di Platone.

Estas ideias alimentam doutrinas filosóficas e esoterismos, de Demócrito aos neoplatónicos e aos gnósticos. Chegam à Renascença com vitalidade. Lembremo-nos como exemplo, que já no Livro X da Politeia (A República), na exposição do "Mito de Er" e no contexto de um Universo pitagórico, matematicamente e geometricamente ordenado, se descreve como a alma individual tem origem celeste e, guiada pelo "daimon", escolhe uma vida e desce pelas esferas planetárias para encarnar o corpo do recém-nascido. A perspectiva gnóstica vai apresentar nuances muito interessantes e perturbadoras. Aqui, o Homem é originalmente imortal e imaterial, Divino, habitando a abóbada acima das esferas planetárias. Por uma ou outra razão, cai deste elevado estatuto, desce pelas esferas planetárias onde vai recebendo de cada planeta um pouco da sua malignidade, encarnando esta vida de tribulações. Na mundividência estóica, os planetas eram governantes divinos e benéficos. Mas para os gnósticos, são os administradores maléficos do mundo físico, do qual o ser humano somente pela gnosis (ascese pelo conhecimento) se pode libertar e almejar a definitiva união com o Divino. (vide McMinn, J. B., A Hellenistic Legacy: The Foundation for an 'Unorthodox' World View within the Byzantine Tradition (part two)", Kernos, 1989).

Na Antiguidade tardia, época de escoliastas (comentadores), epítomes e antologias (florilegia), a mescla de Aristotelismo e Neoplatonismo comum em autores como Proclus foi, segundo Jim Tester, em certa medida, historicamente tão importante como as próprias obras dos grandes filósofos, tal como o De Officiis de Cícero será um dos mais influentes contributos para a formação do alicerce científico e filosófico; e todos os aristotélicos e platónicos tardios denunciam influências e uma fusão com ideias Estóicas e Neo-Pitagóricas. (A History of Western Astrology, Boydell Press, 1999 (1987), p.160).

Um exemplo curioso do recurso ao simbolismo astral é o do Mitraísmo. Embora o deus Mithras ou Mitra (mas não o culto), tenha sido importado da Pérsia, o seu simbolismo astral, bastante óbvio, pertence definitivamente ao mundo da cultura e astrologia greco-romana do Império. (Roger Beck, Mithraism, in Ruggles, (ed.), "Handbook of Archaeoastronomy and Ethnoastronomy", Springer, 2015, p.1670). O Mitraísmo foi uma religião activa no Império Romano desde o início do segundo ao final do século IV d.C. Foi um dos chamados cultos de mistério, um termo aplicado a religiões não oficiais de iniciação (como Roger Beck explica, o termo “culto”, que significa “adoração”, não carregava as actuais conotações pejorativas). Cada culto estava focado num determinado deus ou conjunto de deuses. Assim, os iniciados de Mitra adoravam “o Deus Sol Invicto”, como foi nomeado. O Mithraeum (a caverna, espaço de culto) era, segundo Porfírio (c.234 – c.305 AD), um “Modelo do Cosmos”. Os seus “elementos” eram os signos do zodíaco e os planetas. Os adeptos compartilhavam a crença generalizada de que a alma humana descia à mortalidade terrena através de uma entrada no solstício de verão em Cancer e ascendia de volta à imortalidade através da porta diametralmente oposta, no solstício de inverno, em Capricornus. A chamada "Tauroctonia" é o principal ícone de culto. Mas o que representa o matador do touro? Vários identidades foram sugeridas e a especulação vem de longe. David Ulansey (The origins of the Mithraic mysteries: cosmology and salvation in the ancient world. Oxford University Press, 1989) identificou um deus-constelação Perseus e propôs que o ícone estaria relacionado com a precessão dos equinócios e o deslocamento do Ponto Vernal, sendo a entidade (Mithras-Perseus) quem controlaria este importante processo astronómico. Beck, por sua vez, identificou o "matador" não com um determinado signo/constelação, mas com o próprio Sol num determinado signo significativo: Leo, o Leão. (Mithras in the tauroctony. in: Hinnells J. (ed) "Studies in Mithraism". Bretschneider, Rome, 1994; v. também The religion of the Mithras cult in the Roman empire: mysteries of the unconquered sun. Oxford University Press, Oxford. 2006).

A iconografia é normalizada e verifica-se que os seus elementos parecem representar simbolicamente um grupo de constelações, abaixo do Zodíaco, para leste do Touro até ao Escorpiáo. Os portadores dos archotes (Cautes e Cautopates) ladeiam a composição. (Roger Beck , Mithraism, in Ruggles, C. (ed.), Op. cit., Fig. 150.4)

Muito mais tarde, no saber medievo informado pelo aristotelismo assimilado a partir do séc. XII, os conceitos fundamentais radicavam nas simpatias, antipatias e a na apetência aristotélica pelo "lugar natural". Tudo tem esta "inclinação" para o sítio a que pertence e lhe é conveniente (Lewis, C. S., The Discarded Image: An Introduction to Medieval and Renaissance Literature, Cambridge University Press, 1964, 92). É o que descreve Chaucer (Hous of Fame, II, 730 sq.):

Every kindly thing that is
Hath a kindly stede ther he
May best in hit conserved be;
Unto which place every thing
Through his kindly enclyning
Moveth for to come to.

No "Livro da Montaria" de D. João I, num intervalo da caça ao javali, podemos ver exposto um enquadramento doutrinal da Teoria dos Elementos:

"Ora sabede que diz Joam Gil no seu grande liuro de estronomia, que todallas cousas que som feitas, todas som feitas per natura naturante, que he Deus, ou por natura naturada, que Deus fez , que por elle he ordenada, segundo a ordenaçom que lhe elle pos, a qual ordenaçom chamamos nos outros natureza, (...) E este Deus segundo os philosophos que nom forom hereges, derom hum arneço pollo poder deste Deus, e disserom que elle todo sabedor, e poderoso, pollo seu saber e poder fez de nouo húa matéria, a qual nos nom podemos saber que he, nem de que he, senom que lhe chamam todollos philosophos 'ille', da qual fez os quatro ellementos, e que por esta materia, a que elles disserom ille, e que por esto leuarom elles nome ellementos, destes quatro ellementos segundo os philosophos criou Deus, a que elles dizem natura naturante, todallas cousas que som, também ceeos, como as pranetas, e signos, e estrellas..." (Edição de Francisco Maria Esteves Pereira, Coimbra, Imprensa da Universidade, 1918, pp. 125-6). Adiante referem-se os signos e os "pranetas", que imprimem as qualidades nas coisas sublunares, compostas pelos quatro elementos.

Em termos abrangentes, a Idade Média é uma época livresca e de "autoridades", que se guia pelas Escrituras e pelo Livro da Natureza, com diversas camadas de significação, um universo pleno de símbolos e alegorias. Segundo Jacques Le Goff, o homem medieval habitava uma "floresta de símbolos": "Foi Santo Agostinho que o afirmou: o mundo é constituído por signa e por res, ou seja, por sinais, símbolos, e por coisas". Em resumo, "o homem medieval é um 'descodificador' contínuo". (O Homem Medieval, Editorial Presença, 1989 [L’Uomo Medievale, Gius. Laterza & Figli, 1987], p.27). No aspecto teológico assiste-se à cristianização das esferas. O pseudo-Dionysius viveu nos séculos V ou VI e acreditava-se que os seus trabalhos eram da pluma do próprio Areopagita, convertido por Paulo. Talvez aqui radique a popularidade dos seus tratados teológicos, mormente as suas Hierarquias Celestiais (com os seus Serafins, Querubins, Tronos, etc.), base de toda a ulterior angelologia.

"O homem religioso vive em duas espécies de tempo, a mais importante das quais, o Tempo sagrado, se apresenta sob o aspecto paradoxal de um Tempo circular, reversível e recuperável, espécie de eterno presente mítico que o homem reintegra periodicamente pela linguagem dos ritos." (Eliade, M., Op cit., 82). Assim se vivia o calendário e a renovação cíclica do Homem e do envolvimento, em todas as suas valências. Na Astrologia, traduzir-se-á amiudadamente na horoscopia contínua e cíclica.

O múnus do calendário é, evidentemente, qualificar o tempo. Vamos agora referir alguns ciclos ainda mais ambiciosos.

Aveni argumenta que o objectivo do "jogo" da interpretação dos ciclos cronológicos, em diversas civilizações, por exemplo na China, na Índia (Yugas, “eras”) ou entre os antigos Maias (onde o maior ciclo era o kalpa), seria vincular a duração observável e sensível ao tempo gerido ou "dominado" pelas divindades planetárias.

Os astrólogos da Pérsia vão encontrar um sistema (de raíz astrológica) muito cómodo, através das conjunções dos lentos e ponderosos planetas Júpiter e Saturno (cada qual enquanto chronocrator, "Senhor do Tempo", utilizando a expressão grega). Uma vez que Saturno percorre anualmente cerca de 12° zodiacais, enquanto Júpiter percorre cerca de 30°, uma conjunção média dos dois planetas deverá acontecer, cerca de 20 anos mais tarde, num ponto com uma longitude 240° superior à do ponto em que a conjunção média anterior ocorrera (vide E. S. Kennedy & D. Pingree, The Astrological History of Masha'allah, Harvard Monographs in the History of Science, Harvard University Press, 1971, p.69). Uma concatenação de conjunções percorre os signos de uma Triplicidade astrológica (conjunto dos signos do mesmo elemento: Fogo, Terra, Ar ou Água), mudando de Triplicidade (passando para outro "elemento") após 240 anos. Somente após 960 anos (i.e. 48 conjunções) é que ambos os planetas se conjugam no mesmo signo, na chamada "grande conjunção". Esta doutrina constituirá uma ferramenta cronológica "vaticinadora" de acontecimentos “globais”: alterações dinásticas, religiosas, grandes cataclismos, etc. Fascinou muitos sábios desde então. Os textos de Ja'far ibn Muhammad al-Balkhī (787-886), Abū Ma'shar (conhecido no ocidente como Albumasar), divulgaram-na na Europa. E foi estudada com denodo por tantas mentes brilhantes (Bacon, D'Ailly, Kepler, etc.). Nessa doutrina, assim como os astros nasciam, se levantavam no horizonte, e se punham, assim as cidades, os impérios, as igrejas, floresciam e murchavam, envelheciam e morriam, e às vezes renasciam com "vida nova" (Eugenio Garin, O Zodíaco da Vida: a polémica sobre a astrologia do século XIV ao século XVI, Editorial Estampa, 1987 (1976), p.47). Albumasar também se debruçava sobre a questão do aparecimento dos "profetas" e das religiões, articulando as grandes conjunções com outras variáveis astrológicas que deveriam ser concomitantes (determinados planetas em certas casas significativas, etc.).

"[Roger] Bacon was particularly fascinated with Abū Ma’shar’s teaching that a specific conjunction of Jupiter and Mercury in Virgo had brought about Christianity, and that a similar one of Jupiter and the Moon would bring about the arrival of Antichrist. For Abū Ma’shar the iconography of the decans had been important in this context, because the first decan of Virgo (1°–10°) was represented as a woman holding a child, which Abū Ma’shar interpreted as Mary with the Infant Jesus. This ultimately goes back to the ancient Egyptian iconography of the decans which depicted the first decan of Virgo as Isis holding the child Horus." (Stephan Heilen, "Ptolemy’s Doctrine of the Terms and Its Reception", in: Jones, A., (ed.), Ptolemy in Perspective..., Springer, 2010, p.71)

No que diz respeito à interpretação Renascentista, E. Garin enfatiza a tensão entre "a instância humanista (...) que opõe a obra livre do Homem" e a "concepção de um renascer inscrito num carácter cíclico que parece subordinar qualquer acontecimento da história humana aos movimentos celestes." (op. cit., p.48).

(fonte: North, J. D., Astrology and the Fortunes of Churches, Centaurus 1980: vol. 24, pag.187)

No esquema acima, como exemplo, observamos que a série de conjunções que começa no início de Aries (sendo a primeira identificada como "0") vai percorrendo signos da mesma Triplicidade (Fogo, neste caso) até que na "13" se transita para outro 'Elemento' com a entrada em Taurus (nestas mudanças reside a ancoragem dos grandes eventos históricos). Deste modo, as "grandes conjunções" (i.e., as "normais", de 20 anos, cada qual acontecendo em longitude 117º atrás), resultam após 240 anos numa "conjunctio major" que acontece quando há mudança de Triplicidade (i.e. num signo de outro elemento). Todavia, os cálculos não acontecem com rigor astronómico, pois recorrem ao chamado 'movimento médio' (mean motion, que assume velocidade angular constante numa órbita circular) e não o verdadeiro (que tem velocidade angular variável). Após 960 anos teremos a chamada "conjunctio maxima", quando a série volta à Triplicidade original. A estas últimas foram associados eventos civilizacionais, políticos e religiosos muito relevantes (e.g., o Dilúvio, o advento do Islão, a Reforma, etc.). Não existindo equivalência, é impossível não relacionar este 'desenho' com teorias como o Grande Ano (que referiremos de seguida), com doutrinas do movimento da "Oitava Esfera" (Precessão e Trepidação), com os grandes ciclos planetários ou com as cronologias persas (zoroastrianas, mormente da época Sassânida) e indianas (as Idades cíclicas da cosmologia Hindu: os Yugas). O sistema de conjunções sofreu adaptações ulteriores, e.g., em Pierre D'Ailly (vide Smoller, L. A., History, Prophecy, and the Stars: The Christian Astrology of Pierre d'Ailly, 1350–1420, Princeton University Press, 1994).

Uma das doutrinas cíclicas respaldadas em Albumasar é o chamado "horóscopo das religiões". As conjunções de Júpiter com cada um dos restantes planetas determinariam "Eras religiosas", e dado que são seis planetas, seis serão as Eras e as sectas principales: a conjunção com Saturno, significa livros sagrados e a religião mais antiga, o Judaísmo; com Marte, a "lei" Caldaica que ensina a adorar o fogo, com o Sol é a "lei" Egípcia e a adoração da milícia celeste conduzida pelo Sol, com Vénus é a "lei" venérea e voluptuosa dos Islamitas, com Mercúrio é a "lei" Cristã e com a Lua é a perturbadora "lei" do Anticristo. No séc. XIII, Roger Bacon transcreveu este "esquema" no seu Opus maius. E o cardeal Pierre D'Ailly (1351-1420) não hesitará em admitir a dependência astrológica da própria Encarnação de Cristo!

Foi na abordagem pitagórica (ou neopitagórica, pois a mitificação da figura de Pitágoras pelos seus sucessores tornou-o praticamente "insondável"), que em matéria astronómica se baseou em fontes próximas, que assistimos à especulação em torno do "Grande Ano", conceito platónico decerto remotamente originário da Babilónia, onde provavelmente se baseava nos rácios orbitais dos planetas (i.e., em múltiplos desses períodos). Não se relaciona com a chamada Precessão dos Equinócios, um fenómeno diferente. Para compreender Platão, imagine-se (segundo a comparação de Godefroid de Callatay, professor da UC Louvain) a convergência dos "ponteiros" do grande relógio cósmico, quando os planetas voltam à posição inicial (é o Ano Perfeito, que o filósofo não calcula nem do qual nos dá a demora). O "Grande Ano" e o posterior "Ano Precessional" (que não está relacionado com a astronomia da Mesopotâmia) têm implicações teleológicas, i.e., relacionadas com os fins, as finalidades do Universo. São diferentes entre si mas serão amiudadamente confundidos. Acerca do Grande Ano, desde Santo Agostinho que a perspectiva de um retorno cíclico das sete estrelas errantes [planetas] à mesma configuração era considerada teologicamente "perigosa". Estará mais tarde incluída nas famosas 'condenações' de 219 opiniões pelo Bispo de Paris em 1277. O carácter cíclico contrariava a mensagem Cristã de que a Redenção havia sido possível através do acontecimento histórico, Único, do sacrifício de Cristo. (v. J. D. North, Chaucer's Universe, Oxford, Clarendon Press, 1988, p.37).

Um exemplo da complexidade dos ciclos astrológicos utilizados, e dos intercâmbios culturais em presença, encontra-se no Megillat ha-Megalleh ("O Pergaminho do Revelador") de Abraham bar Ḥiyya (ca. 1065–ca. 1145), obra onde se encontram a astrologia, a ciclologia e o messianismo, a tentativa de previsão da chegada do Messias da Nação Judaica. Segundo J. Samsó (On Both Sides of the Strait of Gibraltar: Studies in the history of medieval astronomy in the Iberian Peninsula and the Maghrib, Brill, 2020, pp.307-8), Bar Hiyya recorre aos seguintes ciclos:

- 4,320,000,000 anos, derivados do Brahmasphuta-siddhānta de Brahmagupta: no momento da Criação, todos os planetas, nos seus apogeus e nodos estavam no início (0º) de Aries, antes de começarem a rodar cada um no seu passo. No final deste período (kalpa) voltarão às posições iniciais;
– 4,320,000 anos (o mahāyuga, igualmente de origem indiana, utilizado no sistema astronómico de Āryabhaṭa, circa 499 A.D.). O número resulta da multiplicação de 360 por 12,000;
– 36,000 anos (33,000 anos na tradução catalã de Millàs Vallicrosa, anota Samsó); [parece derivar da precessão ptolomaica]
– 360,000 anos, o "Ano do Mundo" dos persas, usado por Abū Maʿshar; equivale à duodécima parte do mahāyuga, sendo amiudadamente usado na Astrologia do islâmica como um tasyir [ver técnicas dinâmicas na Astrologia] à escala do Mundo, i.e. "Universo";
– 12,000 anos, correspondendo ao intihā' árabe, também à escala do Mundo [o intihā' "comum" era um ciclo de 12 anos no qual um determinado "indicador" progredia, segundo a técnica dinâmica astrológica denominada progressões, um signo por ano.] Segundo Samsó, é evidente que Bar Ḥiyya confunde aqui dois sistemas: tasyīr e intihāʾ;
– 49,000 anos;
– 7,000 anos.
Estes dois últimos ciclos têm provável origem judaica (relacionados com os conceitos de Ano Sabático e o de Jubileu, respectivamente). Os astrónomos de Alfonso X de Castela utilizaram-nos no modelo da precessão (dos Equinócios) que expenderam, combinando um ciclo regular de 49000 anos com um ciclo de trepidação de 7000 anos.

Quanto às datas prodigiosas inventadas nas cronologias da Antiguidade, já na cronografia do séc. IX escrita por Sincelo (Georgios Synkellos [lit. "colega de cela", cargo que no seu caso dizia respeito ao Patriarca Tarasius]) cronista e eclesiástico oficial (17: "From Africanus, concerning the mythical chronology of the Egyptians and the Chaldaeans"), lemos: "Dos 30000 anos dos Fenícios ou da absurdidade dos Caldeus, com os seus 480000, porque é que alguém deveria sequer preocupar-se em falar?" (v. The Chronography of George Synkellos: A Byzantine Chronicle of Universal History from the Creation, Translated with Introduction and Notes by William Adler and Paul Tuffin, Oxford University Press, 2002, p.23 [trad. nossa]).

Assistimos amiudadamente à crença numa relação de "simpatia" existente entre os corpos celestes e os acontecimentos 'terrestres', base da doutrina astrológica, respaldada em observações que serviam a interpretação de augúrios nas cidades da antiga Mesopotâmia, mais tarde revestida do rigor da geometria grega, de aspectos da filosofia Estóica e de profusos refinamentos árabes. Para além da vertente electiva (katarchai, escolha do "momento propício" para determinada acção), havia assumido, no contexto Helenístico, contornos genetlíacos (referentes ao nascimento, horóscopos individualizados) plenos, vide Holden, James H., A History of Horoscopic Astrology, A.F.A., 2006.

Na antiga Mesopotâmia manifestou-se, como sabemos, a necessidade de registar a configuração e os movimentos dos corpos celestes (traduzidos na significativa metáfora poética da "Escrita do Céu", vide Krupp, Op cit., 1992, p.127; Rochberg, F., The Heavenly Writing, Divination, Horoscopy, and Astronomy in Mesopotamian Culture, Cambridge University Press, 2004), suporte de aplicações do calendário e das prognoses divinatórias relacionadas com o Rei ou a Cidade, motivação para a elaboração de catálogos e tábuas de efemérides para os fenómenos celestes. Nesta perspectiva técnica, segundo Anton Pannekoek (A History of Astronomy, Op. cit., p.80), estamos perante um sistema único (não explicativo dos fenómenos físicos mas sistemático e formal) de representação matemática dos fenómenos: "...Its theory does not imply a new system of world structure, or a physical interpretation, but merely a formal mathematical representation of the phenomena".

Neste contexto cultural já existia um vasto e antigo compêndio de 'presságios' (Enuma Anu Enlil). Por volta do primeiro milénio século antes da nossa Era, surgem os MUL.APIN, textos cuneiformes em placas de barro com informação específica e técnica. O nome "MUL.APIN" remete para o respectivo incipit, as palavras de abertura da listagem de estrelas e asterismos, literalmente "Estrela do Arado", a primeira entrada, padrão associado ao início do ano (que incluiria estrelas da actual constelação Triangulum e ainda Gamma Andromedae). O importante catálogo foi copiado até à época Helenística e teve grande influência e disseminação. Começa com a lista de estrelas e grupos de estrelas associados aos três caminhos (faixas de latitude celestial em que dividia o céu, atribuídas, de Norte para Sul, às divindades Enlil, Anu e Ea), descreve pares de constelações em função da posição simultânea no zénite e no horizonte (entre outras correspondências), inclui considerações acerca do movimento dos planetas, elenca as constelações no "caminho" percorrido pela Lua e ainda expõe um "calendário sideral", no formato a que os Gregos chamaram parapegma [etimol. "colocar uma pega (ou estaca) ao lado de..."; plural: parapegmata], que permitia determinar/assinalar as datas no ano através da verificação do nascer helíaco (data da primeira visibilidade no horizonte leste antes do orto solar), do ocaso de determinadas estrelas, etc. (Evans, J., The History and Practice of Ancient Astronomy, Oxford University Press, 1998, 5 et seq.).

"Another common feature of public places was the parapegma – a sort of star calendar. A parapegma listed the heliacal risings and settings of prominent stars and constellations in the order of their occurrence during the year. Often, but not always, these were accompanied by notices of seasonal changes (beginning and end of the season for Zephyros, the west wind, or for the Etesian winds). And many parapegmata also predicted individual rainstorms. A parapegma could be a text written on papyrus, but in its original form it was a public document, engraved in stone. A small hole near each line of writing allowed the insertion of a wooden peg that could be moved along from one day to the next." (James Evans, Material Culture of Greek and Roman Astronomy, in C.L.N. Ruggles (ed.), "Handbook of Archaeoastronomy and Ethnoastronomy", Springer, 2015. vol.3, ch. 141, p.1594)

"Parapegmata are among the oldest astronomical instruments from the classical world, and are closely related to the earliest astronomical/astrological tradition in Greece, that of stellar astrometeorology." (Daryn Lehoux, Image, Text, and Pattern: Reconstructing Parapegmata, in: Jones, A. & Carman, C. (eds.) "Instruments - Observations - Theories: Studies in the History of Astronomy in Honor of James Evans", ISAW, 2020, p.109)

"O ciclo dos aparecimentos e desaparecimentos das estrelas fixas constituíam uma parte importante na antiga astronomia, tanto grega como babilónica. Como exemplo, tome-se o caso das Plêiades. Durante a Primavera, as Plêiades desapareciam durante um mês e meio quando o Sol, no seu percurso pela eclíptica, se aproximava delas. Depois (em finais de Maio), as Plêiades emergiam do seu intervalo de invisibilidade. Podiam ser observadas, pela primeira vez, nascendo do oriente, poucos minutos antes da aurora. Era o nascimento matinal das Plêiades. Assinalava a época da colheita do trigo e o início do tempo de Verão. Do mesmo modo, o aparecimento matinal de Arcturus era reconhecido em todo o mundo Grego como assinalando o início do Outono. Os nascimentos e ocaso das estrelas que acontecem imediatamente antes do nascimento do Sol, ou imediatamente a seguir ao seu ocaso, são chamados nascimentos e ocasos "helíacos" (porque acontecem relativamente ao Sol). São também chamadas "fases" das estrelas fixas. Por volta do século V aEC ["antes da Era Comum", BCE no orig.; na prática = a.C.], estas tradições foram sistematizadas no parapegma, ou calendário estelar. (O calendário das estrelas era um pouco mais antigo entre os Babilónios. A compilação MUL.APIN, do século sétimo, já incluia um calendário deste tipo.) Um parapegma listava os nascimentos e ocasos helíacos das estrela pela ordem cronológica. O utilizador saberia a altura do ano verificando que estrelas ascendiam ao início da manhã. Este tipo de calendário era um suplemento para os caóticos calendários civis dos Gregos. Amiudadamente, mas nem sempre, as "fases das estrelas" faziam-se acompanhar de predições metereológicas. Podia-se facilmente compilar uma lista de nascimentos e ocasos helíacos das constelações, simplesmente através de observações na alvorada e no crepúsculo, efectuadas ao longo de um ano. Não havia necessidade de qualquer tipo de 'teoria'. Neste sentido, o parapegma pode ser considerado 'pré-científico'. Todavia, compreender o ciclo anual das "fases" foi um importante desiderato da mais antiga astronomia científica grega. De facto, um dos mais antigos trabalhos que sobreviveu da sua astronomia matemática é dedicado a este assunto. Trata-se do livro (na realidade são dois) escrito por Autólico (Αὐτόλυκος) de Pitane [Πιτάνη] por volta de 320 aEC e chamado "Dos Nascentes e dos Poentes". Autólico define os vários tipos de nascimentos e ocasos heliacais, depois estabelece e prova teoremas relacionados com a sua sequência no tempo e o modo como a sequência depende da posição da estrela em relação à eclíptica. Nenhuma estrela individual é especificamente nomeada. O objectivo é disponibilizar uma teoria para o entendimento dos fenómenos." (Evans, J., The History and Practice..., Op. cit., p.190 [trad. nossa]).

Outra referência é a obra de (ou atribuída a) Ptolomeu: Phaseis ou "Fases" das Estrelas Fixas (Gr. Φάσεις ἀπλανῶν ἀστέρων καὶ συναγωγὴ ἐπισημασιῶν, "Das aparências das estrelas fixas e colecção de prognósticos"). Consiste em dois livros que estudam os nascimentos e ocasos das estrelas e a sua influência metereológica. Apenas o livro II (um parapegma precedido por uma introdução) sobrevive em Grego e foi esta versão incompleta que foi traduzida em Latim nos séculos XVI e XVII. Excertos de ambos os livros originais foram perpetuados em Árabe.

Para Geminus (Γεμῖνος, Rodes, séc I a.C.), as estrelas somente indicavam, não determinavam os fenómenos metereológicos. Em termos populares e no enquadramento astrológico seria diferente. Como não relacionar os parapegmata com os ulteriores almanaques e repertórios? Encontraremos conteúdos astro-meteorológicos em Plínio, o Velho (Naturalis Historia, lib. XVIII) ou Columella (De Re Rustica, lib. XII), sem esquecer "Os Trabalhos e os Dias" (Ἔργα καὶ Ἡμέραι, romaniz.: Érga kaì Hēmérai) do arcaico Hesíodo, remoto antecedente. Um formato que se tornará mais sofisticado e se revelará perene e popular.

Na astrologia medieval, por exemplo, o chamado 'ingresso' em Aries (Equinócio Vernal) era fundamental na antecipação do novo ano e previsão da abundância ou carência de produtos agrícolas, sua qualidade e preços, questões de "saúde pública", etc. Observava-se particularmente o horóscopo da lunação que precedia este ingresso (o mesmo, sem a mesma imporância para as restantes Estações). Mas existia uma dualidade de procedimentos entre o uso do horóscopo da lunação ou o do momento (conjunção) propriamente dito.

Após a delineação do Zodíaco, e ampliando o escopo da vasta literatura de augúrios genéricos ou respeitando o rei e a cidade, surge na Mesopotâmia uma horoscopia individual. Segundo Francesca Rochberg (Op. cit., p.121):

"Por volta do final do século V a.C., a julgar pela aparência de horóscopos cujo desígnio seria a determinação de aspectos da vida individual a partir dos sinais celestiais, acreditou-se que os céus significavam, não somente para o rei e o país, como acontecia no tradicional corpo textual dos augúrios, mas também para qualquer indivíduo. Poucos dos horóscopos que conhecemos contém detalhes acerca da vida do nativo, todavia todos informam a data de nascimento. A intenção é, portanto, inequívoca. A horoscopia cuneiforme baseava-se, obrigatoriamente, na disponibilidade de registos planetários e lunares e não na observação, pois nem todos os planetas estariam sempre observáveis acima do horizonte no momento do nascimento, e obviamente nem todos os nascimentos acontecem à noite. Pretende-se pois (neste capítulo) demonstrar a dependência babilónica relativamente a uma variedade de textos preditivos, observacionais e astronómicos. Assim se sugere que os escribas que gizaram os horóscopos, apesar de competentes nas metodologias da ciência dos astros (ou assim podemos assumir), não calculavam as posições planetárias directamente nos horóscopos, antes recorrendo a uma ampla escolha de textos astronómicos à sua disposição enquanto materiais de referência." [trad. nossa]

(...) esos orbes de diamantes,
esos globos cristalinos,
que las estrellas adornan
y que campean los signos,
son el estudio mayor
de mis años, son los libros
donde en papel de diamante,
en cuadernos de zafiros,
escribe con líneas de oro,
en caracteres distintos,
el Cielo nuestros sucesos
ya adversos o ya benignos...

"Les infatigables "Égyptiens" [i.e. gregos ou 'helenizados' no Egipto Helenístico] poussaient bien plus loin les spéculations sur les couleurs du Soleil et de la Lune, non seulement pendant les éclipses (e.g., Hephaest., I, 21), mais au lever, au coucher des luminaires, ou même "pendant tout un jour". Le Soleil, sans être éclipsé, peut être "terni" au point de ressembler à un miroir, ou à une Lune, et de laisser voir des « astres » en plein jour; il peut être ocreux ou rouge au point que le sol a des reflets sanguinolents; tout cela, selon le signe où il se trouve, a un sens et une adresse." (Bouché-Leclercq, L'Astrologie grecque, 1899, pp.355-56)

Para o classicista, filólogo e historiador Franz Boll (1867-1924), a Astrologia era o mais peculiar "centauro" (um ser híbrido) alguma vez produzido pela religião e pela ciência. E num epítome feliz de A. Aveni, "após seguirmos as imagens, acreditámos nas imagens" (Op cit., 1994, ch.5). Cada lugar pertencia a um signo e a um elemento, estando ainda associado ao predomínio dos planetas (consoante fosse o lugar estivesse na sua casa, exaltação, termo, etc.); cada estrela (luminares e planetas) possuía as suas qualidades elementares, dignidades essenciais (designadas "quilates" pelos nossos tratadistas do séc. XVII) e acidentais (estas últimas em função da geometria [e.g., os aspectos, relações agilizadas em intervalos de 30 graus: sextil 30º, quadratura 90º, trino 12º, oposição 180º], e da presença "em corpo" em determinado lugar). A Lua, a estrela mais próxima e intermediária por excelência, presidia aos ritmos e "canalizava" os "influxos". Luna, Selene, Cynthia... "fria e húmida", presidia sobre as águas:

...the moist star,
Upon whose influence Neptune's empire stands.
(Shakespeare, Hamlet, Act.1 Scene.1)

Numa das suas mais perenes associações, a Astrologia aplicada à Medicina (Iatromathematica, do Gr. yatrós, "médico" e mathematica: os astrólogos eram μαθηματικοί, matemáticos) articulava-se com a Teoria dos Elementos e reflectia-se nas quatro “virtudes” dos seres vivos, expressas por Galeno: a atractiva (quente e seca), a digestiva (quente e húmida), a expulsiva (fria e húmida) e a retentiva (fria e seca):

"Every living being, plants as well as animals, was provided by the Creator with the four ‘natural faculties’ of attraction, assimilation, excretion and growth. Each part of the body had thus the potentiality, as a result of its elemental organisation, to feed on this nutritious blood, to assimilate whatever it needed to grow and to function, and to excrete potentially harmful residues that it no longer needed. The body was a living universe, responding to changes and actively seeking whatever it needed in order to exist and to function." (Nutton, V., Ancient Medicine (2nd ed.), Sciences of Antiquity, Routledge, 2013, p.239)

Era, tradicionalmente, através do ciclo da Lua que se fazia a análise da evolução das doenças. Os chamados Dias Críticos eram fortes indicadores para se perceber se o doente recuperava ou sucumbia. Contavam-se a partir da "idade" (em dias) da Lua no início da doença (decumbitura), quando o doente se recolhia ao leito e deitava. Eram também os dias em que o physicus ou o medicus previa o aparecimento de uma crise.

Gravura que acompanha o capítulo "De anima vitalis cum intellectuali Scientia, hoc est, de Genethlialogia" (Tomi secundi, tractatus primi, sectio secunda de technica microcosmi historia) do monumental e eclético Utriusque cosmi, maioris scilicet et minoris... ("Dos dois Mundos, nomeadamente do Maior e do Menor..."), de Robert Fludd (Oppenheim, J. Theodor de Bry; Hieronymus Galler (impr.), 1617-21)

O historiador Kocku von Stuckrad (História da Astrologia: da Antiguidade aos nossos dias (Geschichte der Astrologie, Verlag C. H. Beck oHG, 2003); trad. Kelly Passos, São Paulo, Editora Globo S.A, 2007) procurou fazer uma leitura a partir do conceito de "tempo interpretado" e cita Anthony Grafton: "A continuidade da tradição astrológica é única na história das humanidades no mundo ocidental". Quanto ao tempo qualificado, a astrologia postula uma correspondência entre os níveis celestial e terrestre, uma correspondência que é construída basicamente sobre analogias simbólicas. Salienta que os astrólogos não foram unânimes ao julgar como essa correspondência se realizava - se existia uma sincronia misteriosa, uma interligação geral de todos os seres, ou se os astros influenciavam a Terra de maneira causal. No enquadramento nas disciplinas esotéricas, e atendendo à periclitância da definição do termo, Stuckrad respalda-se na definição através da qual Antoine Faivre propôs descrever o esoterismo como uma "forma de pensamento no qual a realidade é concebida de um modo específico". Essa definição heurística foi apresentada nos anos 90 do século passado. Algumas características básicas são aqui resumidas:

- Pensar em termos de correspondências (diferentes níveis de "classes" da realidade), visíveis e invisíveis estão ligadas por um elo; O Universo é visto como uma espécie de teatro de espelhos onde todas as coisas podem conter referências a outras coisas;
- A ideia de natureza viva entende o Cosmos como sistema complexo, dotado de alma e banhado por uma energia viva;
- Imaginação e mediações indicam que o conhecimento acerca das correspondências exige imaginação simbólica ou revelação por "autoridades espirituais";
- A experiência da transmutação cria um paralelo entre a acção exterior e a vivência interior (evoca-se o exemplo da Alquimia).

Aos traços "intrínsecos" já expostos, Faivre acrescentou mais dois elementos: 1) a prática da concordância esforça-se em encontrar um denominador comum ou “origem primordial” e 2) o conceito de transmissão ou iniciação.

Hermes representado num mosaico renascentista do pavimento da Catedral de Siena (Giovanni di Stefano, 1488). O mítico sage é aqui apresentado como "Hermes Mercurius Trimegistus contemporaneus Moisy" , i.e. "contemporâneo de Moisés" e suposto profeta de Cristo, prestigiosa informação que radica numa equivocada e "forçada" interpretação que recua a Lactâncio (Lucius Lactantius, autor cristão do séc. IV), vide Roelof van den Broeck, Wasn't Hermes a prophet of Christianity who lived long before Christ?, in: Hanegraaff, W, Forshaw, P. & Pasi, M., (eds.), "Hermes Explains: Thirty Questions about Western Esotericism", University of Amterdam Press, 2019, pp.54-60

É neste ponto que Stuckrad argumenta que a Astrologia é uma "disciplina-chave" dentro do conjunto de tradições esotéricas. Deve-se, sobretudo, à sua "neutralidade" e "abstracção", já que trabalha com um número limitado de “princípios cósmicos primordiais', que são suficientemente amplos para serem aplicados em concretizações diversas, como o princípio “inibidor” ou o princípio “propulsor”, mas permitem, ao mesmo tempo, uma grande variedade de combinações. As interpretações astrológicas baseiam-se em combinações sempre novas de um número limitado de elementos. O historiador conclui o seu estudo subscrevendo o que "Girolamo Cardano já sabia no século XVI: a astrologia não é uma ciência matemática, e sim hermenêutica". Não mede o tempo, interpreta o tempo.

Relacionando judiciosamente a origem da horoscopia com a filosofia e a cosmologia, Richard Gordon resume: "Most Hellenistic philosophers allowed that Fate was inexorable and granted it some limited place in their cosmological schemes. All these sytems in turn were heavily indebted to the rationalisation of the cosmos as a (benignly ordered) geo‒centric system developed by Eudoxus of Cnidus and Callippus of Cyzicus in the mid‒fourth century BCE, and progressively refined thereafter. With the impetus provided by the Babylonian calculation of solar, lunar and planetary positions, standardised in ephemerides (handy tables), the concept of the fixed zodiac, and primitive ‘horoscopes’ based on the day, month and year of birth, all of them schemes and techniques mediated into Greek in Seleucid Babylonia, the various modes and techniques of Greek horoscopal astrology were created – that is ‘emerged’, since all relevant names are pseudonyms such as ‘Zoroaster’, ‘Hermes’, ‘Nechepso’, ‘Petosiris’, even ‘hierogrammateis’ (i.e. senior Egyptian temple‒priests) ‒ no doubt in Alexandria, during the later third and second centuries BCE. This intense pseudonymous/anonymous labour produced what is today known as the ‘Hellenistic vulgate’. The notion of an immutable futurity, what the IVp author Firmicus Maternus terms fatalis necessitatis lex, a fixed law of absolute necessity, was generally asssumed by practitioners to be basic to the entire project of using the heavenly bodies ‒ regarded as visible divinities whose predictable movements follow unchanging laws - as a reference - point for divination. This was of course to pitch the claim to have found a means of rationalising uncertainty at the highest conceivable level, above all when it was a matter of the major art, that of genethlialogical astrology, the art of casting nativities for the entire life of an individual. The result, inevitably, was not merely a flight into complexity but an assiduous lack of interest in the theoretical underpinnings – a practitioner such as Vettius Valens in the High Empire could write an entire handbook of genethliacal astrology without once mentioning the problem of mediation, that is, how the stars affect human life." (Will my Child Have a Big Nose?: Uncertainty, authority and narrative in katarchic astrology, in: Rosenberger, Veit (ed.), "Divination in the Ancient World: Religious Options and the Individual", Franz Steiner Verlag, 2013, pp.97-98)

O estatuto "científico" da Astrologia remonta aos primeiros horóscopos babilónicos do séc. V a.C. [Pingree chama-lhes "proto-horoscopes" (pois horoscopia, por definição, pressupõe o recurso ao ponto ascendente).] Na Mesopotâmia, tudo aponta para uma prática astrológica através de augúrios, baseada em "sinais" e "indicadores" de origem divina, não uma dinâmica de causalidade directa. Após a definição de um sistema de "marcadores" e da invenção do zodíaco, as passagens dos luminares e planetas de um para outro signo eram provavelmente muito relevantes astrologicamente (O. Neugebauer, HAMA, p.412). A Lua, por exemplo, era observada no seu movimento, na região do céu que atravessava, na direcção em que era observada e na fase; mas também a coloração e tonalidade, a aparência dos seus "cornos", o eventual brilho da região não iluminada (se envergava um agu, "tiara" ou "manto real"), eventual coroa de luz ou halo (vide Pannekoek, p.43). O vasto acervo de antigos augúrios, muitas vezes copiado, está na origem da compilação de setenta tabuínhas conhecida como Enuma Anu Enlil (Rochberg, F. (1988), Babylonian Horoscopes, Transactions of the American Philosophical Society, 1998, x). A partir de finais do séc. V a.C. surgem na Babilónia provas arqueológicas da prática de uma "horoscopia" individual, que influencia mas é todavia diferente da helenística em muitos detalhes, e.g., ênfase na hora e não num ponto ascendente da eclíptica, diferente abordagem cosmológica/filosófica/religiosa, etc. (ibid., pp.1-2). O texto dos exempla disponíveis é lacónico. [Os "horóscopos" mesopotâmicos não podem tecnicamente ser classificados como uma modalidade de horoscopia (ou astrologia horoscópica), pois não recorrem aos anguli (particularmente ao ascendens) ou à domificação (divisão das 'casas' ou loci).]

Entretanto, na época helenística floresce uma literatura astrológica escrita em Grego, que aglutina elementos mesopotâmicos, egípcios e gregos. Os chamados "Livros Herméticos", que contém toda uma teologia baseada num misticismo astral vão disseminar-se pelo mundo romano (vide Lloyd-Jones, Hugh, Myths of the Zodiac, Gerald Duckworth & Co., 1978). O determinismo de raíz Estóica e a religião astral da Mesopotâmia eram "aliados naturais". A astrologia helenística respalda-se no conceito de um Kósmos interdependente, enformado por princípios de "simpatia" e correspondência, do qual o ser humano é parte integral. Nela encontramos um reflexo da physis grega, da teoria dos elementos e da geometria.

Afirmação de poder recorrendo ao simbolismo astrológico. Molde do "Horóscopo do Leão", por Karl Humann, 1883 (Staatliche Museen zu Berlin). O Horóscopo do Monte Nemrud (Nemrut Dağ, em Turco) de Comagena (pequeno reino helenístico com capital em Samosata). Parece celebrar o reconhecimento pelos romanos do rei Antiochos I (séc. I a.C.). Trata-se de uma estela (laje de pedra mede 2,40m por mais de 1,80m de altura) de um conjunto de cinco. O relevo, astrologicamente relevante, representa um Leão onde se sobrepõem dezanove estrelas. Assim, Regulus (gr. Βασιλίσκος "a estrela régia"), visível acima do crescente lunar, assinala apropriadamente o "coração" do poderoso animal. Em cima, à esquerda, são representados os planetas Marte, Mercúrio e Júpiter, identificados por inscrições (F. K. Dörner, J. H. Young, Sculpture and Inscription Catalogue, in: Donald H. Sanders, "The Hierothesion of Antiochos I of Commagene", Eisenbrauns, 1996, pp.252–54). Segundo Otto Neugebauer e H. B. van Hoesen (Greek Horoscopes, pp.14-16), horóscopo foi calculado tropicalmente (não sideralmente) segundo a convenção dos signos utilizada na Mesopotâmia ou pelo "esquema" de Eudoxus (em causa a convenção para o grau de início de cada signo, v. pág. Esfera), e refere-se a uma data equivalente a 7 de Julho de 62 a.C.

Na opinião de A. Pannekoek, a partir da abordagem grega, os planetas já não são "sinais" mas sim "causas": "(...) now that the planets had become world bodies describing their orbits in space, calculable by theory, their character had changed; their course was not a sign but a cause of the happenings on earth." (Op. cit., p.131). Como J. Tester resumiu (A History of Western Astrology, Boydell Press, 1999 (1987), p.59), a filosofia grega incluia a ponderação racional do mundo físico. E a Astrologia somente se desenvolve plenamente a partir da racionalização de um Universo ordenado e inteligível. Os Elementos e as Qualidades serão pivotais. A doutrina dos elementos é mais antiga do que a Filosofia. Segundo o que podemos inferir, no séc VI a.C. Tales de Mileto adoptou a 'Água' como elemento primordial, Anaxímenes o 'Ar' e Heráclito o 'Fogo'. Os dois últimos pré-socráticos faziam derivar os outros elementos a partir da 'primeira matéria'. O Ar, a Terra e a Água representavam os três estados comuns testemunhados (gasoso, líquido e sólido, respectivamente). O Fogo era diferente: provenienente de matéria sólida, extinguido pela água, simulltaneamente fonte de luz e calor [As chamas que vemos provêm do fogo impuro, e é essa imperfeição que o torna visível. O Fogo no estado puro, elementar, situa-se imediatamente abaixo da esfera da Lua, é não adulterado e totalmente transparente]. Um quinto elemento foi imaginado pelos pitagóricos: o Éter, qual "fogo celeste", provavelmente porque, estando filosoficamente respaldados na Matemática, no Número, quiseram que se verificasse uma equivalência com os cinco sólidos regulares (i.e. de faces iguais), um para cada "elemento" (cubo-terra, pirâmide-fogo, octaedro-ar, icosaedro-água e dodecaedro-éter). Mais importante, os pitagóricos "canonizaram" outra doutrina ancestral, a dos 'Opostos': um-muitos, limitado-ilimitado, ímpar-par, macho-fêmea e por diante. Estas polaridades e complementaridades percorrem a filosofia grega e, particularmente, a sua Medicina. Foi Zenão de Eleia que a partir de dois pares destes opostos (quente-frio e húmido-seco), criou o resto a partir deles. E Aristóteles, na sua Física, coalesceu as duas doutrinas e gizou os seus quatro "corpos simples": Fogo, Ar, Água e Terra a partir de, respectivamente: 'quente e seco', 'quente e húmido', 'frio e húmido' e 'frio e seco'. (De Gen. et Corrup., II). Alguns estóicos interpretaram, simplificando as equivalências: fogo-quente, ar-frio, água-húmido e terra-seco. Os elementos, as qualidades e os opostos passaram a fazer parte dos alicerces do pensamento clássico tardio, especialmente na Medicina. E foram esses mesmos estóicos que tornaram praticamente unânime outra importante doutrina: a Unicidade do Cosmos (incluindo o Homem). Todas as coisas, afirmavam, estavam ligadas pela mesma energia cósmica, ou logos, "razão" [conceito de um Cosmos interdependente]. Coube a Ptolomeu, no espírito filosófico e científico da sua época, coligir no seu influente tratado astrológico estes princípios considerados "coerentes" e racionais.

Filosoficamente, a recepção desta mundividência foi multifacetada (seguimos resumo do enquadramento filosófico e científico também gizado por Tester):

Uma corrente estruturante com enorme 'autoridade' era, obviamente, a dos Aristotélicos (os Peripatéticos) do "Lyceum". Duas escolas ou "seitas", os Cépticos e os Cínicos, eram naturalmente adversos à Astrologia. Os seguidores de Platão, na Academia, eram muito mais abertos, tendo assimilado conceitos de outras correntes filosóficas e místicas. Entretanto, duas influentes escolas na percepção que viremos a ter do Homem e do seu lugar no Mundo serão a Epicurista e a Estóica. A primeira, cujo pensamento conhecemos principalmente a partir do De Rerum Natura, de Lucrécio (Lucretius) era ateísta e materialista (admitindo somente a existência dos "átomos" e do "vazio"), demarcando-se de intervenções divinas e "supersticiosas" e promovendo a tranquilidade através da indiferença ou ausência de medos (ataraxia) e do sofrimento físico (aponia), cultivando a serenidade e o conhecimento dos limites para os desejos. Era prática e empirista, rejeitando obviamente a Astrologia pelo seu vínculo às aspirações e emoções humanas. O Estoicismo era tecnicamente "materialista" mas com nuances. Não admitia a separação entre a matéria e o espírito. Adoptaram os quatro elementos e ainda o quinto elemento subtil ("aether", o éter), provavelmente por via aristotélica. Para os estóicos, a alma era material mas mais subtil, interpenetrando o corpo e, após a morte, voltando ao ambiente etéreo dos céus. A mundividência era fatalista, regulada pela ideia de Destino e de uma "simpatia cósmica" que era, deste modo, perfeitamente compatível com a Astrologia. Adequou-se, principalmente pelos ensinamentos de Posidonius, ao modus Romano, com o seu sentido do dever perante o Estado e da participação política. (Op. cit., pp.51-2; 59-60).

A Astrologia sumariza, como vimos, contributos das diversas culturas intervenientes. No princípio reside a concepção Babilónica de que a configuração dos céus e os fenómenos astronómicos (e meteorológicos) concomitantes com o nascimento do indivíduo fornecem uma base para o prognóstico da sua vida. Do Egipto adapta o antigo conceito de "observação da hora" (que acontecia recorrendo a um sistema de decanos), segundo o qual os pontos do Zodíaco que sucessivamente atravessavam o horizonte ou o meridiano 'significavam' e qualificavam esses momentos específicos. Formatada por conceitos gregos, continuará no período bizantino e será extremamente apelativa para as culturas islamizadas. Chegará, através da vasta literatura dos seus tratados, ao Ocidente Latino.

A origem da chamada horoscopia helenística (i.e. prática astrológica individualizada baseada na "tetralogia" Planetas - Signos - Lugares (as "Casas", "loci") - Aspectos, recua aos textos em grego, redigidos no Egipto, que se reclamam da "linhagem" dos considerados "Antigos" (em rigor, trata-se e autores dos séculos I e II a.C. que se ocultam sob os nomes prestigiosos de Hermes-Asclepius-Nechepso-Petosiris, etc.), amiudadamente citados nos textos dos séculos I e II A.D. Esta modalidade combina, no mínimo, contributos mesopotâmicos, egípcios e gregos:

"Esta forma de astrologia, chamada genetlíaca, possui raízes na física aristotélica e na astronomia helenística, mas também tomou emprestado muito da Mesopotâmia e alguns elementos do Egipto, desenvolvendo outrossim muitas teorias próprias. A adaptação destinada à determinação dos momentos propícios para encetar acções designa-se astrologia dos começos [Gr. καταρχή, "katarchai": a astrologia electiva, que repousa num sistema de "cronocratorias", influência preponderante de um "mestre do tempo"]. Estes são os dois principais ramos da astrologia conhecidos no Ocidente. A astrologia das interrogações foi desenvolvida na Índia nos séculos II e III A.D. tendo como base a astrologia electiva grega; e a astrologia histórica surgiu no Irão sassânida provavelmente nos séculos V e VII A.D., respaldada nas modalidades 'contínuas' da genetialogia grega. Todos estes tipos de astrologia dependem da noção de que os planetas, na sua eterna rotação em torno da Terra, transmitem movimento (mudança) aos quatro elementos aos e compostos destes elementos, animados ou inanimados, no mundo sublunar. Esta teoria é completamente diferente da dos augúrios celestes, na qual os deuses, que se manifestam fisicamente através das constelações e dos planetas, enviam mensagem dizendo respeito aos reis e às regiões através de fenómenos celestes. Que estas intenções divinas possam ser alteradas pelo recurso a rituais propiciatórios ('namburbis' na Mesopotamia, sãntis ["pacificação"] na India) enfatiza a diferença conceptual fundamental entre augúrios e astrologia." (David Pingree, From Astral Omens to Astrology (From Babylon to Bikaner), Roma: Istituto Italiano Per L'Africa e L'Oriente, 1997, pp. 21-22 [trad. nossa])

O nosso conhecimento é provisional e sempre condicionado pela leitura dos intérpretes gregos. Daí a referência a uma "miragem" do Egipto, preteritamente estudado somente "de fora" (perspectiva actual enfatiza o "transaccional" e "dialógico", e.g., em Ian Moyer: Egypt and the Limits of Hellenism, Cambridge U. P., 2011). Ainda se discutem as contribuições específicas de cada uma destas culturas, bem como a cronologia da evolução ou do aparecimento de conceitos e técnicas fundamentais. Em todo o caso, esta "arqueologia" padece de lacunas documentais que impedem uma delineação clara das fontes e da tramitação do conhecimento. Muitos conceitos (para além dos inequivocamente documentados, como o do zodíaco esquemático) parecem possuir um precedente (ou um paralelo) mesopotâmico (e.g., as 36 estrelas de referência podem ter tido uma função análoga à dos decanos, parece existir um esboço das chamadas "triplicidades", etc. Mas o que distingue a sofisticada abordagem helenística, formalizada nos autores dos séculos I e II, é a ênfase geométrica numa estrutura esférica, tridimensional (não apenas aritmética como no Oriente Próximo), o eclético suporte filosófico grego, particularmente o Aristotélico (evidente em Ptolomeu), conceitos pitagóricos, platónicos e a mundividência estóica, o recurso ao conceito dos quatro elementos e suas qualidades, etc. O período entre o aparecimento da astrologia natal (não horoscópica) na Mesopotâmia (durante a dominação Aqueménida) e esta modalidade mais "sofisticada" está pouco documentado. Antes disso, como sabemos, temos o que parece ser a origem da Astrologia: a prática da observação e dedução de augúrios patrocinada pelo poder instituído, desde os séculos VII ou VIII, profusamente documentada nas bibliotecas de placas cuneiformes.

Os Aspectos, relações geométricas fundamentais na abordagem astrológica (Auguste Bouché-Leclercq, L'Astrologie Grecque, Paris, E. Lerous, 1899, p.173)

Jean-Patrice Boudet resume o contexto medieval (dos primórdios à retoma da tradição):

"A Astrologia Bizantina, muito dinâmica na esfera dos horóscopos políticos a partir do séc. V, beneficia dos contribulos Islâmicos a partir do séc. VIII. Floresce até à queda de Constantinopla (séc. XIV) através da escola de Johannes Abramius. No Ocidente latino, a situação é radicalmente diferente até ao começo do séc. XII, pois os trabalhos dos matemáticos gregos e árabes eram quase desconhecidos. Durante a Alta Idade Média, a astrologia não foi considerada muito diferente da adivinhação por augúrios, consequentemente patrísticamente condenada. Modalidades muito simplistas, traduzidas do grego, floresceram a partir do séc. VIII: esferas de "vita e mors" (atribuídas a Pitágoras, Petosiris ou Apuleio), prognósticos baseados num ciclo lunar imaginário de 30 dias ("lunaria") ou nas posições zodiacais do Sol e da Lua (zodiologia) [Filões de literatura técnica com origem na Antiguidade tardia, muito comuns no ocidente na Alta Idade Média; eram populares e assoberbados pela ingenuidade de uma época da qual não se conhecem horóscopos ou nomes de astrólogos.] Na ausência de tabelas astronómicas e instrumentação, a horoscopia foi ignorada até à segunda metade do séc. X, com o aparecimento de um 'corpus' designado "Alchandreana", parcialmente traduzido do árabe, que permitia gizar horóscopos segundo princípios numerológicos. A disponibilidade de um 'corpus' astrológico informado, veiculando um sistema hierarquizado de conhecimento e levando em consideração um elevado número de parâmetros, aconteceu somente a partir do séc. XII com as traduções latinas de tratados que divulgaram as regras, tabelas astronómicas e instrumentos exigidos à prática da horoscopia e dos 'julgamentos'". ("Astrology", in: Glick, T., Livesey, S. and Wallis, F., Medieval Science, Technology and Medicine, An Encyclopedia, Routledge, 2005, p.61 et seq. [trad. nossa]. Boudet ainda refere (ibid.), relativamente a um período mais recente, que "adeptos de uma visão muito determinística, tais como Abu Ma'shar (Albumasar), séc. IX, e os seus seguidores italianos do séc. XIII, Guido Bonatti e Pietro D'Abano, puderam (nesse contexto), ser confrontados com alguns dos maiores adversários da possibilidade divinatória astral: o médico Avicena, o historiador ibn Khaldun (séc. XIV), os franceses Nicole Oresme (1322–1382) e Jean Gerson (1363-1429) ou o italiano Pico della Mirandola (1463-1494)."

O poeta e filósofo platónico Bernardus Silvestris (séc. X), autor de um prosimetrum (texto em prosa e verso) sobre a criação do mundo, descreve como a figura simbólica da "Mente" ou "Inteligência" do Universo (gr. νοῦς, nous) desvela como o céu, na sua polimorfa variedade de imagens, é como um livro aberto contendo o futuro inscrito em letras crípticas, reveladas (somente) perante os olhos dos mais sábios. Hugo de São Victor (no seu Didascalicon, c. 1129) definiu a Astronomia como a lei das estrelas e a Astrologia como o discurso que concerne às estrelas. Mas os mais influentes enciclopedistas medievais discutem a Astrologia de um modo que sugere uma familiaridade superficial e uma ténue consciência do que esta de facto pressupõe. Preservam o claro confinamento dos "poderes" das estrelas ao "corpóreo" (saúde, meteorologia e assim por diante), não envolvendo a determinação do destino da vida. Estes relatos surgem, amiudadamente, no âmbito de considerações acerca de assuntos como o herbalismo, a geomancia (essa "combinaison d'astrologie, d'arithmétique et de loterie", segundo Bouché-Leclercq) ou a numerologia. O que vemos emergir no século XIII, com o advento do aristotelismo, é a perspectiva de que ciências (no sentido lato da época), como a Astrologia, funcionam porque são mecanismos naturais concebidos por Deus para o governo da sua Criação. Um conhecimento natural independente da Revelação a partir do qual o intelecto humano pode inferir o carácter do Criador. A Astrologia será pois uma faceta da visão da Natura como entidade autónoma, criada para operar de modo racional. Poderia, deste modo, ser articulada com a doutrina Cristã. O sábio Inglês Robert Grosseteste (c. 1168-1253) declara como a Natureza precisa do apoio da Astronomia (Astrologia), pois há poucas operações no seu seio que não estejam sob a sua orientação quando transitam de potência a acto. Exemplifica com o crescimento das plantas, a transmutação dos metais e a cura das doenças.

A Astrologia assumirá as duas vertentes: "natural" e "judiciária". Uma reflecte a inquirição no âmbito da Philosophia Naturalis ou estudo do "Livro da Natureza". A segunda foi desde cedo e amiudadamente proscrita (leis e diatribes contra os mathematici, genethliaci e prognosticadores, documentados deste a época Clássica). Entretanto, o sistema é integrado na doutrina Cristã, salvaguardando o fundamental livre arbítrio (as decisões individuais que determinavam tranquilidade ou danação ad aeternum).

Na mundividência medieval, a alma é distinguida em três componentes ou modalidades hierarquicamente organizadas: "thre manere soulis . . . vegetabilis that geveth lif and no feling, sensibilis that geveth lif and feling and nat resoun, racionalis that geveth lif, feling, and resoun." (Bartholomaeus Anglicus, De Proprietatibus Rerum). Ou seja, a vegetativa, a sensitiva e a racional, esta última exclusiva do ser humano.

Assim, a "influência" dos astros restringe-se aos eventos corpóreos (na Summa Contra Gentiles, Tomás de Aquino é taxativo: "é impossível que a operação do intelecto esteja sujeita aos movimentos celestes" (III. 84)): trata-se apenas de Causas Secundas, em relação à Divina Providência, a "Causa Primeira". Num exemplo extraído da chamada "Crónica de Portugal de 1419", um conselheiro de D. Afonso IV toma a palavra: "Senhor", diz, "os sabedores que amte nós forom, aynda que às costelações [i.e. configurações astrológicas] grande poderio dessem, nom leyxarom porem de asynar livre alvidro [alvedrio, arbítrio], ho qual muitas vezes pode fazer as costolaçoes serem verdadeyras. E, posto que elas sejam juizes de inteligemçias que naturalmente mentir não podem, o sobrenatural Regedor as priva muytas vezes de seus naturaes efeytos por responder com justiça aos mereçimentos do livre alvidro...". Um pouco adiante: "E, pois que as costelaçoes e fados sam findos e a graça de Deos he infinda, ho infindo de neçesidade vemçerá o que for findo. fazendo çesar a costelaçao de sua detreminada obra." (Crónica de Portugal de 1419, ed. crítica de Adelino de Almeida Calado, Aveiro, Universidade de Aveiro, 1998, pp.242-3).

Contudo, foi sendo paralelamente sugerido que os poderes dos signos e dos planetas seriam, na realidade, "pessoais", espíritos (daemones) que podiam ser invocados (v. por exemplo o Liber Intelligentiarium de Antonius de Monte Ulmi (Montuolmo), activo em Bolonha por volta de 1380). De resto, assistimos a curiosas "acomodações" das práticas religiosas à Astrologia. Como exemplo, o astrólogo da corte de Mântua Pellegrino Prisciani (1435–c.1518) aconselha a Marquesa Isabella d’Este Gonzaga a encetar as suas orações apenas no momento da benéfica configuração da chegada da 'Cauda do Dragão' (Cauda Draconis, um dos nodos lunares) ao ângulo culminante (meio-céu ou summum coeli) pois aumentará a eficácia (Graziella Federici Vescovini, The Theological Debate, p.117, in: Dooley, B. (ed.), "A Companion to Astrology in the Renaissance", Brill, 2014 ; ver também: Sophie Page, Magic in the Cloister. Pious Motives, Illicit Interests, and Occult Approaches to the Medieval Universe, University Park, Pennsylvania State University Press, 2013). O compreensível desconforto da Igreja com estas elucubrações que ultrapassavam a vertente "natural" expressa-se, mais tarde, na bula papal Coeli et Terrae (expendida por Sisto V em 1586). A sua base doutrinal remete para o princípio de que somente Deus pode conhecer o futuro, condenando liminarmente a judicatura. Em 1633, Urbano VIII emite a bula Inscrutabilis, na qual as prognosticações acerca das crises na Igreja e nos reinos são particularmente visadas. (v. Whitfield, Op. cit., 2001, p.163)

Entretanto, tudo se alterará na chamada "Idade Moderna", com o novo paradigma científico e o ideário das 'Luzes'. Pierre Gassendi (1592-1655) já manifesta a nova "atitude científica". No Livro VI do seu Syntagma philosophicum, t.I, pt. 2a, Sect. II, questiona quais os efeitos que as estrelas produzem nas "regiões inferiores" e como se produzem. É consensual que o primeiro efeito é a luz, especialmente a do Sol; calor-secura e frio-humidade provêm da Terra. E estes determinam os efeitos secundários do tempo e das estações. São óbvios mas indiscriminados e gerais, acontecendo aqui e agora de modo puramente acidental. O futuro pode ser conhecido a partir das causas, e.g., a Primavera significa que as flores vão desabrochar; ou sinais, e.g., a aurora significa que o Sol vai nascer. Se a predição astrológica não se enquadra em qualquer destas, não é praenotio (conhecimento antecipado) mas conjectio (palpite). Adiante refere que existem, claro, causas pelas quais cada homem (indivíduo) é como é, mas estas residem nos próprios indivíduos e neste mundo, não nas estrelas. A única maneira de discernir que influências dos céus se verificam na Terra é o 'modo científico', através de Observantia nempe sive Experientia ("nomeadamente observação ou experiência"). (v. Tester, Op. cit., 231-32). Como von Stuckrad resume, o lugar do Homem como centro da Criação perder-se-á. Da Antiguidade até o século XVII havia, a bem da verdade, um consenso de que as Leis do Céu e da Terra seriam basicamente diferentes [as "Duas Naturezas", a elementar e a etérea], como Aristóteles ensinara. Somente o mundo sublunar estaria exposto às leis da mudança e da decadência. Como consequência da nova filosofia, graças à igualdade de leis terrestres e celestes, o estudo das coisas comuns pode esclarecer as características universais do Cosmos. Desse modo, tanto a divisão aristotélica entre matéria e forma foi abalada, como também a opinião de que existiam conexões ocultas (e.g., simpatia). De acordo com a visão de mundo mecânica (pós-newtoniana) doravante defendida, somente explicaçòes físicas, como a gravidade das partículas, podem ser consideradas em tais ligações. Não pode haver dúvida acerca do efeito radical do novo pensamento. (Op. cit., p.279 et seq.)

Um aspecto curioso diz respeito à suposta "história milenar" da Astrologia. O problema é antigo. No De Divinatione (tratado em dois livros sob a forma de um diálogo) de Cícero, é referida como inverdade a antiguidade da astrologia dos Babilónios, que recuaria a 470 000 anos (I. 19; Ed. Loeb), durante os quais teriam sido feitos os horóscopos de todas as crianças e testados os seus resultados (II. 46). Seriam 473 000 anos segundo Diodoro (Diodorus Siculus, II. 31). Estes valores recuam a Berossus (Gr. Βηρωσσος; um acreditado "sacerdote de Bel-Marduk" helenizado que se instalou na ilha grega de Kos no séc, III a.C.) e variam segundo os autores que os citam. Simplikios (Lat. Simplicius, comentador do séc. VI) parece ter acreditado numa antiguidade ainda maior. Segundo Bouché-Leclercq, o egípcio Manéthōn e Berossus parecem "competir" entre si, afirmando a prioridade do Egipto ou da Mesopotâmia, respectivamente. No entanto, mesmo os autores menos crédulos acreditavam estar perante uma tradição antiga e os gregos assumiam tranquilamente o papel de "aprendizes": "Les Hellènes se prêtaient d'eux-mêmes à ce rôle de néophytes" (L'Astrologie grecque, p.35). Algumas "Histórias da Astrologia" não somente suportam acriticamente episódios sobre "vaticínios" que na realidade foram forjados a posteriori (logo retrospectivos ou confirmatórios) como dão eco a cronologias fantasiosas, embora não rivalizando com Firmicus Maternus (autor do Liber Matheseos, conhecido como Mathesis ou De Nativitatibus, séc. IV), e outros no que respeita à informação da prodigiosa "antiguidade" das "observações" caldaicas. Há também, desde o séc. XIX, toda uma literatura com enfoque nas manifestações culturais e iconografia de diversas civilizações em resposta ao deslocamento do ponto Vernal (Precessão dos Equinócios) e das diferentes "Eras Zodiacais", projectando no passado espantosas datações e até argumentando um (extremamente improvável) conhecimento científico arcaico desse fenómeno (é a tese de Giorgio de Santillana e Hertha von Dechend em Hamlet's Mill, Boston, Gambit, 1969).

A tendência para a fantasia continua, sem os exageros pretéritos mas com a mesma falta de rigor nas inúmeras obras de divulgação contemporâneas. Joanna Woolfolk, no best seller "The Only Astrology Book You’ll Ever Need (Taylor Trade Publishing, 2008), escreve estas coisas notáveis (p. 371):

"The path of the stars was recorded 6,000 years before Christ was born. As early as 2767 b.c., a horoscope was cast in Egypt by Imhotep, the architect of the great Step pyramid in Saqqarah. That horoscope still exists! Ancient astrologers charted the movement of planets and stars, and made predictions about eclipses, upheavals, famine, and fortune. They developed calendars for marking and measuring the passage of time. You can still read star charts that were made by Egyptian astrologers in 4200 b.c. In ancient societies, astrology and religion were inextricably linked." [Na realidade, os horóscopos, ou mesmo o Zodíaco dividido em doze sectores de 30º cada, não existem antes do séc. V a.C., o horóscopo de uma natividade mais antigo que conhecemos data de 410 a.C. (Rochberg, Babylonian Horoscopes, p.3) e a horoscopia genetlíaca como a reconhecemos, de matriz greco-egípcia, surge somente no período Helenístico. A referência a Imhotep deve ter saído de um mau argumento de Hollywood!]

Convém não esquecer a chamada "Astrologia Védica" (na realidade não se encontra qualquer vestígio de horoscopia nesses antigos textos) e que por vezes se reclama de uma antiguidade assombrosa, baseada nos ciclos temporais míticos das tradições religiosas do Indostão (e.g., yugas, manvantaras) e numa interpretação literal das antigas epopeias. Impregnados de um nacionalismo pouco saudável, alguns praticantes fazem recuar a origem da sua astrologia (supostamente autóctone e independente de influências "bárbaras") tão cedo que receamos recuar ao Cretácico ou até à própria origem do Sistema Solar! Um perfeito absurdo que não faz justiça às influentes e riquíssimas culturas em causa que, não sendo estanques, tanto receberam como exportaram (o sumamente importante "zero" é conceito indiano, bem como tantas ideias e elucubrações religiosas e filosóficas, o infinito do próprio Tempo (Kãla, também associado à morte), as ideias-base teosóficas, novas sensibilidades nas cogitações científicas (por exemplo a influência no trabalho de Fritjof Capra et al.) e nas crenças do quotidiano de tantos e tantos seres humanos pelo mundo fora). Muitos académicos indianos não estão isentos desse complexo, dirigindo amiudadamente investigações no sentido de "provar" a prioridade dos textos da sua tradição.

Description de l'Égypte, A. vol. I, planche 79: Esné (Latopolis): Zodiaque sculpté au plafond du portique. (ed. C. L. F. Panckoucke, 1820). O magnífico Zodíaco linear de Esna é um dos únicos três preservados em templos Egípcios [clicar para visualizar com maior resolução]. Ver esquema com a suposta identificação dos signos.

Na prática, foram gizados vários sistemas de referência para documentar a dinâmica observada nos céus. O "Zodíaco" na Mesopotâmia, as "Mansões Lunares" (nakshatras) na Índia e os "Decanos" no Egipto. Dignum memoria, Otto Neugebauer elencou-os:

Three different systems of astronomical reference were independently developed in early antiquity: the "zodiac" in Mesopotamia, the "lunar mansions" in India, and the "decans" in Egypt. The first system alone has survived to the present day because it was the only system which at an early date (probably in the fifth century BC) was associated with an accurate numerical scheme, the 360-division of the ecliptic. (Neugebauer, O., The Egyptian "Decans", "Vistas in Astronomy" (ed., A Beer), vol. 1, Pergamon Press, 1955; repr. in Astronomy and History: Selected Essays. Springer, 1983, 205)

Matematicamente, segundo Neugebauer, (...) a Astronomia mais primitiva concentrou-se, principalmente, no enquadramento dos fenómenos tendo como referência o Horizonte, enquanto em períodos mais tardios se respaldou em menos óbvios mas bem mais convenientes sistemas de coordenadas, nomeadamente a Eclíptica e o Equador [i.e. baseados nestes círculos]. Todavia, tal como em muitas outras circunstâncias, é a Astrologia que vai perpetuar conceitos antiquados, determinando a sua sobrevivência até em tratados estritamente técnicos. É provavelmente por esta razão que o Almagesto expõe, logo após o catálogo de estrelas (VIII, 5) o problema da determinação do ponto da Eclíptica que nasce em simultâneo com determinada estrela. As estrelas que nascem simultaneamente são chamadas "paranatellonta" e a doutrina astrológica associa as suas qualidades e influências como o ponto correspondente da Eclíptica. (A History of Ancient Mathematical Astronomy, Springer-Verlag, 1975, p.39; [trad. nossa])

Como Petra Schmidl explica, os doze signos podem ser vistos como "as doze mansões mensais" do Sol. Mensalmente (aproximadamente), o Sol muda de mansão. Analogamente, as mansões lunares podem ser vistas como "as vinte e oito mansões diárias" da Lua, que após um mês parece retornar à mesma, Na sua função enquanto "zodíaco lunar" as mansões puderam ainda ser utilizadas, do mesmo modo que os signos, os decanos egípcios ou as estrelas ziqpu ("culminantes") babilónicas, como marcadores da passagem do tempo e referências do calendário. (Elections in Medieval Islamic Folk Astronomy, in: Burnett, C. & Greenbaum, D. G. (eds.), From Masha'Allah to Kepler: Theory and Practice in Medieval and Renaissance Astrology, Sophia Centre Press. 2015). O termo Manãnzil já é citado no Kur'an (X, 5; XXXVI,39).

Num estudo com algumas décadas (Chaucer's Universe, Oxford; Clarendon Press, 1988), J. D. North afirmava que o sistema possuia obviamente raízes arcaicas sendo provavelmente pouco pertinente procurar um único centro de difusão ("...it is probably a mistake to look for a unique centre of diffusion.", p.246). A divisão do tempo baseado na passagem da Lua através das estrelas é [decerto] pré-histórica, e encontrada em culturas cujas competências astronómicas são, de resto, rudimentares. Uma vez que a Lua percorre a eclíptica em aproximadamente 27 dias e meio, não surpreende que tenham sido atribuídos nomes a essas 27 ou 28 regiões entre as estrelas, cada qual ocupada supostamente pela Lua durante 1 dia. O sistema chinês de hsiu é equatorial enquanto o indiano se baseia na eclíptica. Desenvolveu-se autonomamente, difere do sistema indiano (que se tornou influente na astrologia "Ocidental") na sua lógica interpretativa e nas divisões que estabelece e servia uma espécie de hemerologia de dias fastos ou nefastos, bem como os augúrios relacionados, por exemplo, com as diversas regiões do Império. Ainda segundo o autor, numa época ainda pré-Islâmica, os árabes adoptaram da astronomia indiana um sistema sistemático e organizado ["manazil", nakshatras no original]. As estrelas de demarcação no esquema indiano foram escolhidas de modo a ficarem situadas a alguma distância na Eclíptica, para poderem funcionar como "marcadores" estando visíveis apesar do brilho da Lua (esta afasta-se da eclíptica até dez dos seus diâmetros, pelo que as estrelas de referência idealmente estariam afastadas em função dessa distância). Quanto à sua recepção no Ocidente Latino, por via da influência dos tratados em Árabe. (Op. cit., p.246)

North comentou ainda as disputas de mais de um século visando a atribuição da prioridade da implementação do sistema (com a China e a Índia na dianteira), afirmando que a verdadeira origem do debate recua à recolecção de informação por al-Biruni, académico, astrónomo e viajante na Índia do início do século XI (pp.246-47). Bouché-Leclercq (no clássico L'Astrologie grecque, p.463, n.2) refere que o autor Islâmico Haly: "...assure que les Arabes ont emprunté le système des 28 mansions aux Hindous, qui l'avaient pris "dans les livres de Dorothée [Dorotheus de Sídon]." (cf. Haly filii Abenragel, scriptoris Arabici, de judiciis astrorum libri octo..., (cap. 100); ed. P. Liechtenstein, 1571). Contudo, a difusão de um remoto precedente mesopotâmico prevaleceu nas argumentações académicas, sendo referido como possibilidade na Encyclopaedia Britannica (em linha): "In India a complete list of nakshatra are found in the Atharvaveda, providing evidence that the system was organized before 800 BCE. The system of lunar mansions, however, may have a common origin even earlier in Mesopotamia". Mas uma origem paralela e independente é, porventura, muito provável. A origem indiana da implementação prevalecente parece-nos provável e foi também veiculada por O. Neugebauer (v. citação supra).

Disposição das "Mansões Lunares" (Philip Yampolsky, The Origin of the Twenty-Eight Lunar Mansions (Osiris, vol. 9 (1950))

Para Daniel Martin Varisco, o termo Árabe "manāzil" (habitualmente traduzido "mansions", mansões) será mais adequadamente traduzido (em Inglês) como "station" [talvez "estação" ou "paragem" em Português] (Illuminating the Lunar Mansions (manāzil al-qamar), in: Šams al-maʿārif, Arabica 64 (2017), Brill, p.488, n.1) Enquanto os asterismos não definem porções iguais (pois não estão naturalmente localizados a distâncias uniformes), o modelo astronómico faz equivaler cada "mansão" a um arco com 12°51’ (360° / 28). Uma vez que o "caminho da Lua" se situa sempre até 5º da eclíptica, os asterismos situam-se quase todos em constelações zodiacais. (Varisco, p.492). As "mansões" foram associadas pelos antigos autores árabes às tradições relacionadas com a meteorologia das anwāʾ (sing. nawʾ) [um sistema autóctone arcaico de marcadores] ainda na época pré-Islâmica. (ibid., p.493). O mesmo autor refere que alguns textos divinatórios em Árabe promoverão a sua associação com letras, aromas, formas geomânticas e a predição dos momentos propícios ou nefastos para determinados empreendimentos (ihtiyārāt, equivalendo a 'hemerologia' ou ao Lat. electiones).

O Zodíaco é aquela faixa percorrida "activada" pelos luminares e pelos planetas. "Círculo inclinado", caminho rigoroso do Sol, é também aí que os planetas fazem os seus percursos, se aproximam e afastam, interagem. Qualquer calendário mede os movimentos dos luminares nessa faixa. Bartel van der Waerden, no clássico History of the Zodiac (Archiv für Orientforschung, 1953), explicou que a ideia de fazer corresponder os meses e as constelações recua a listagens datadas na proximidade do 1º milénio a.C., associando a cada mês as estrelas ou constelações que nele nasciam. Mas a correspondência seria imperfeita. A utilização de constelações nas imediações da eclíptica será mais pormenorizada, e quase perfeita com a introdução dos signos zodiacais com igual dimensão. Enquanto na astronomia geométrica grega o enfoque será nos solstícios e equinócios [que são pontos "imateriais"], os babilónios calculavam as posições dos planetas e luminares aritmeticamente, de maneira "sideral" [i.e., baseados nas estrelas reais, observáveis], sem destaque para os referidos pontos imateriais de intersecção com o Equador Celeste. Há, de facto, uma diferença entre as mundividências e metodologias babilónica (anterior à Antiguidade tardia) e grega. Pode ser entendida analogicamente como a diferença entre a aritmética e a geometria-cinemática. Como Francesca Rochberg explica em Periodicities and Periodic Relations in Babylonian Celestial Sciences ("Studies in Ancient Magic and Divination", vol.6: In the Path of the Moon Babylonian Celestial Divination and Its Legacy, Brill, 2010), a metodologia babilónica debruça-se sobre a recorrência dos fenómenos celestes num enquadramento temporal e posicional, munindo-se exclusivamente de técnicas aritméticas. O próprio conceito de sítio ou posição de um planeta no zodíaco estava relacionado com a data/hora que lhe correspondia. Cada divisão em 30º de um signo era somente uma baliza ou referência aritmética que não se respaldava numa estrutura cosmológica e geométrica como na astronomia grega, na qual as posições significavam longitudes num grande círculo que bissectava algo que concebiam como "esfera celeste". Por outras palavras, ambas as culturas (babilónica e grega) concebiam um "zodíaco" (i.e. doze segmentos de 30º no percurso do Sol sobre o fundo de estrelas), mas o que este representava era diferente em cada uma dessas culturas. A analogia com o movimento de um corpo segundo um percurso circular definível relativamente a um centro (órbita) não era feita pelos astrónomos babilónicos, antes preocupados com o retorno de determinados fenómenos a certas direcções no céu, calculando a sua periodicidade. Não há uma "eclíptica" nem uma "esfera celeste" como na geometria esférica grega. Isto, como Noel Swerdlow enfatizou, torna a ideia de um movimento contínuo ao longo de um percurso circular totalmente irrelevante para a prática babilónica. Ainda segundo este autor (The Babylonian Theory of the Planets, Princeton University Press, 1998, p.34) e também segundo John Steele (Celestial Measurement in Babylonian Astronomy, "Annals of Science", 64 (2007), pp. 293–325), seria falacioso considerar o zodíaco babilónico equivalente ao de Ptolomeu ou ao moderno sistema de "longitudes" eclípticas. De facto, havia não só uma diferença cosmológica fundamental mas também na própria noção de "círculo" que, como Eleanor Robinson refere (Words and Pictures: New Light on Plimpton 322, American Mathematical Monthly, 109 (2002), p. 111), era para os babilónios definido pela circunferência a partir "de fora", não a área definida pela rotação do seu raio ("de dentro para fora", por assim dizer). A astronomia babilónica determinava datas e posições dos fenómenos, a grega postulava uma cinemática de movimentos uniformes (àngulos iguais em tempos iguais) quando observados a partir do centro da esfera.

"Os signos zodiacais babilónicos" segundo Franz Xaver Kugler (Sternkunde und Sterndienst in Babel (Buch I), Aschendorffsche Verlagsbuchhandlung, 1907, p.30). Colunas: signo, transcrição (que denuncia respectivos "marcadores", e.g., "mulmullu" (sumeriano MUL.MUL, "as estrelas", designava as Plêiades; em acadiano era zappu, "a cerda", reforçando a referência ao chamado "Touro do Céu"), designação actual (latina) e os intervalos em graus com valores reduzidos para a epoch de 1800 A.D.

Na prática mesopotâmica antiga, circa 700 a.C., era utilizada uma faixa zodiacal com determinado número de asterismos e constelações, de dimensão desigual, percorrida pelos luminares e pelos planetas. As primeiras evidências directas ao Zodíaco propriamente dito, como sistema de referência, recuam ao séc. V a.C.: "The earliest direct evidence for the existence of the zodiac comes from fifth-century astronomical diary texts (e.g., No. -453 iv 2 and upper edge 2–3, No. -440 rev. 3', and No. -418:5, 10, rev. 8' and 14') and horoscopes (BH 1 and 2, both dated 410 b.c.), in which positions of the planets are cited with terminology used with respect to zodiacal signs as opposed to zodiacal constellations." (The Heavenly Writing, Cambridge University Press, 2004, p. 130. Esta fundamentação inclui dois horóscopos datados de 410 a.C. (BH 1 e BH 2, editados por Rochberg: Babylonian Horoscopes, Philadelphia, Transactions of the American Philosophical Society, Vol.88, Pt.1, 1998)

Ainda no séc. XIX, Franz Kugler (Babylonische Mondrechnung, 1900), verificou que existiam na Mesopotâmia "tardia" (época Selêucida) dois diferentes métodos para a descrição dos movimentos da Lua. Nestes esquemas, o equinócio (vernal) correspondia no "Sistema A" à posição solar 10º Aries, e no "Sistema B" a 8º Aries (sistemas têm designações convencionais criadas pela historiografia incumbente). Portanto, estes antigos astrónomos simplesmente fixavam os 'marcadores' sazonais no 10º ou no 8º grau dos signos que marcavam o início das estações (vide Neugebauer, The Alleged Babylonian Discovery of the Precession of the Equinoxes, JAOS 70 (1950), pp.1–8).

A divisão que antecede o modelo zodiacal dos signos teve decerto um enfoque lunar, através de 17 ou 18 “marcadores” do caminho da Lua, o 'viajante' mais rápido ("marcadores" na eclíptica a que J. Epping chamou "Normalsterne" em Astronomisches aus Babylon, 1889). Nicholas Campion (Babylonian astrology: Its origins and legacy in Europe, in: H. Selin (ed.), Astronomy across Cultures: The History of Non-Western Astronomy, Dordrecht: Kluwer Academic, 2000), refere que na lista dos grupos de estrelas (a partir de inscrições MUL.APIN, ver infra) deste autêntico "zodíaco lunar", surgem nomes equivalentes aos "nossos" Taurus, Gemini, Cancer, Leo, Libra, Scorpio e Capricornus. As estrelas “no caminho da Lua” (harrãn Sin) eram reconhecidas pelo menos desde o segundo quarto do primeiro milénio a.C. e eram definidas, numa tradução aproximada, como "os deuses que ficam no caminho da Lua, nas regiões que esta atravessa ao longo do mês..." (vide Rochberg, Op. cit., pp. 127-28). O sistema zodiacal mesopotâmico parece evoluír a partir de uma estrutura pretérita desse tipo:

Before the introduction of the zodiac, the Babylonians used a number of constellations to locate bodies in the sky. For example, in MUL.APIN' the path of the moon is traced through 17 constellations. By the fifth century B.C., this had been reduced to 12 constellations. Finally, shortly before 400 B.C., these 12 constellations were replaced by the 12 equal divisions of the ecliptic into the signs of the zodiac. (Lis Brack-Bernsen e Hermann Hunger, The Babylonian Zodiac: Speculations on its invention and significance, Centaurus 1999: Vol. 41, p.280).

Mazzaroth (Hebreu: מַזָּר֣וֹת, mazzārōṯ, LXX (Septuaginta) Μαζουρωθ, Mazourōth) é uma palavra hebraica que surge no Livro de Job (38:32). Surge apenas uma vez em toda a Bíblia Hebraica (ou seja, é um "hapax legomenon"). Desconhece-se o significado preciso (para alguns é uma "guirlanda", "cintura" ou "coroa") mas surge num contexto que refere as constelações astronómicas, podendo significar o Zodíaco ou as suas constelações. Segundo G. Schiaparelli. foi esta a opinião adoptada por S. João Crisóstomo e pela Vulgata, disseminando-se a partir daí (L'Astronomia Nell'Antico Testamento, Milano: Ulrico Hoepli, 1903, pp. 99-100). Em muitas versões da Bíblia grafa-se tão somente "constelações": "...Ou produzir as constelações a seu tempo, e guiar a Ursa com seus filhos?". Schiaparelli, todavia, inclinou-se para uma hipótese que associava o termo ao planeta Vénus, interpretando-o nas suas aparições matutina e vespertina, no contexto mesopotâmico da tríade Shamash-Sin-Ishtar. Mas a associação às constelações e até ao Zodíaco em particular parece concitar um assinalável suporte.

O círculo foi dividido na Mesopotâmia em 360º (mais tarde estruturado em "parcelas" de 30º em consonância com o calendário solar anual composto por doze meses, como Aratus referirá), chegando até nós através da designação grega, transliterada como "Zodiakos". Este, conduzido pelo círculo da Eclíptica, será chamado Circulus signifer ou Orbis signiferus por Cícero e Vitrúvio, poeticamente Media Via Solis, o Balteus stellatus de Manilius ou o varii Mutator Circulus anni de Lucano. Ptolomeu utiliza a designação "eclipticos" somente na relacionação com os eclipses. A eclíptica é sempre (no seu texto), "o círculo inclinado através do meio dos signos zodiacais" (C. J. Toomer 1984, p.20 [trad. nossa]). Cleomedes designa a eclíptica heliakos kuklos, "o círculo do Sol", que é "o círculo no meio da faixa do Zodíaco" (I.2.43–59). Não havendo evidências inequívocas de um conhecimento pretérito, a constatação da sua obliquidade é atribuída pelos próprios gregos a Oenopides de Quios (Chios). Na sua interpretação, Aristóteles associava a estabilidade (a permanência) ao ciclo diurno do Sol, a geração e a corrupção ao seu movimento anual no círculo oblíquo da eclíptica (De generatione et corruptione, 2.10).

A evolução para uma divisão em doze sectores de 30º está também relacionada com a determinação das horas (divisão de cada um dos períodos, diurno e nocturno, em 12 horas sazonais (ou desiguais, pois são variáveis ao longo do ano ao contrário das horas equinociais que hoje utilizamos), um signo zodiacal demorando aproximadamente duas destas horas a ascender). Aratus, no poema Phainomena, faz eco desta utilização. Na opinião de van der Waerden, documenta-se a implementação de "esquemas zodiacais" nos calendários gregos, através dos quais se dividia o ano em 12 meses artificiais ("artificiais" relativamente aos meses lunares habitualmente utilizados) durante os quais o Sol percorria sucessivamente cada um desses signos. O conceito também tem origem na Mesopotâmia. Ainda segundo van der Waerden, os gregos adoptaram esta estrutura e estes signos, alterando o nome do primeiro, a que chamaram Aries, o Carneiro. Hiparco, Geminus, Ptolomeu e Teão (Θέων) teriam utilizado um zodíaco tropical, vinculando o início, por regra, ao Equinócio Vernal. Eudoxus e Aratus, todavia, utilizaram um zodíaco sideral (baseado nas estrelas, nas constelações reais). Este último sistema, utilizando habitualmente o 8º grau de Aries como início (tal como utilizado num dos dois sistemas babilónicos já referidos), permaneceu popular por muito tempo. Vettius Valens (astrólogo helenístico do séc. II) afirmou utilizar tabelas de Apolónio, acrescentando 8 graus aos seus valores (Kroll, Vettii Valentis Anthologiarum libri, Berolini; Weidmannos, 1908, p. 354). Ou seja, sendo as tabelas calculadas tropicalmente, Valens convertia para valores siderais.

Aratus ainda se refere inequivocamente aos sidéreos, às constelações concretas, cada uma com a sua dimensão, enquanto Hiparco, no único dos seus trabalhos que sobrevive (justamente o Comentário de Aratus e Eudoxus) assume (e.g., 2.1.14) uma metodologia diferente: os signos zodiacais medem exactamente 30º cada, dividindo o Zodíaco em doze signos matemáticos e permitindo o cálculo das posições das estrelas em graus e até fracções de grau. (Kidd, D, (ed., trans,), Aratus: Phaenomena, Cambridge Classical Texts and Commentaries, Cambridge University Press, 1997, p.379). É provável que Eudoxus, relativamente ao Zodíaco, também se refira às constelações e tenha assumido, por conveniência, que cada uma ocupe 1/12 do círculo, mas é improvável que tenha utilizado um sistema de arcos de 30º, que não está documentado antes do séc. II a.C. (Dicks, D. R., Journal of Hellenic Studies 86, 1966, 27-8; Early Greek Astronomy to Aristotle (London 1970, p.157). A divisão uniforme em sectores de 30º permitiu a utilização de um sistema de coordenadas (Kelley, D. e Milone, E., Exploring Ancient Skies - A Survey of Ancient and Cultural Astronomy, Springer, 2nd ed. 2011, 28). As 12 constelações adoptadas formaram os signos. A longitude passará a ser medida em graus, a partir do ponto vernal para Leste, ao longo do círculo pertinente, medindo com precisão os movimentos graduais para leste (excepto nas retrogradações) dos planetas e luminares, cada qual no seu "passo".

- Os nomes gregos e latinos dos doze signos (os dodecatemorion de Ptolomeu) são os seguintes: Κριός (Krios) - Aries, Ταύρος (Tauros) - Taurus, Δίδυμοι (Didymoi) - Gemini, Καρκίνο (Karkinos) - Cancer, Λέων (Leõn) - Leo, Παρθένος (Parthénos) - Virgo, Ζυγός (Zygos) - Libra, Σκορπιός (Skorpios) - Scorpio, Τοξότης (Toxotẽs) - Sagittarius, Αιγόκερως (Aegokerõs) - Capricornus, Υδροχόος (Hydrochoõs) - Aquarius, Ιχθύες (Ichthyes) - Pisces.

Como curiosidade, a associação de Cristo com o signo zodiacal Libra (a "Balança") foi considerada tempestiva tendo em vista as ideias de Julgamento Divino e a pesagem dos pecados, e recua pelo menos à época Patrística. (W. Hubner, Zodiacus Christianus, Konigstein, Anton Hain, 1983, passim, em especial p.121)

O Zodíaco (Le grand Kalendrier et compost des Bergiers..., impresso por Nicolas le Rouge, Troyes, 1496)

Milton (Paradise Lost, Book X) faz intervir directamente o Ser Supremo na origo da obliquidade da Eclíptica, causa das estações do ano e das mudanças:

Some say, he bid his angels turn askance
The poles of earth twice ten degrees and more
From the sun's axle; they with labour push'd
Oblique the centre globe: some say the sun
Was bid turn reins from th'equinoctial road
Like distant breadth to Taurus with the seven
Atlantic Sisters, and the Spartan Twins,
Up to the Tropic Crab; thence down amain
By Leo, and the Virgin, and the Scales,
As deep as Capricorn, to bring in change
Of seasons to each clime; else had the spring
Perpetual smil'd on earth with vernant flowers,
Equal in days and nights...

Em Árabe, o zodíaco designa-se mintaqat al-buruj ("o círculo das casas"). Os doze signos são (por ordem): al-hamal, al-thawr, al-jawzã' (ou al-tawa' mãn), al-saratãn, al-asad, al-'adharã, al-mīzãn, al-'aqrab, al-rãmī, al-jadī, sãbik al-mã e al-samakatãn. Na China, este círculo era chamado a "Estrada Amarela" (Kelley, D. e Milone E., Op cit., 26). Segundo Aveni, num estado com uma burocracia rigorosa, os chineses do séc. IV a.C. seguiam a Lua num sistema de 28 marcadores ou “estações” (hsiu ou xiu) análogo às “mansões lunares” para acautelarem os assuntos oficiais. Sistema privilegiado apesar de já conhecerem a divisão duodecimal do ano solar (Op cit., 151).

Os povos da Mesopotâmia utilizavam o Touro e as Plêiades como marcadores do Equinócio de Primavera, compatíveis com a localização vernal numa época recuada. O seu zodíaco seria sideral (guiando-se pelas constelações "reais"). São os gregos que o "fixam" aos pontos tropicais, às estações (zodíaco tropical), implicando o lento "desfasamento" relacionado com o fenómeno da Precessão dos Equinócios (v. infra).

As constelações zodiacais equivalentes entre a Mesopotâmia e a Grécia são, segundo B. van der Waerden: o "Touro do Céu" (Taurus); os Gémeos (Gemini); o Leão/Leoa (Leo); a Espiga de uma deusa "dos grãos" ou "das colheitas", i.e. agrária (equivalente a Virgo); o Escorpião (Scorpio), o Centauro "arqueiro" (Sagittarius), o Capricórnio (Capricornus) e os Peixes (Pisces). A constelação vernal Aries, o Carneiro parece ser de origem helénica, substituindo uma antiga imagem oriunda das margens do Eufrates. (Science Awakening II. The Birth of Astronomy. Leyden: Noordhoff, 1974, pp.287–288)

Shamash (o Sol) surge no Portão Oriental, entre as montanhas (em baixo ao centro), figura emanando raios a partir dos seus ombros. Ishtar (Inanna na Suméria; Vénus) recebe o Sol enquanto "estrela da manhã" (as setas atrás das asas podem representar o seu brilho). À direita, as águas com peixes, fundamentais para a vida, fluindo dos ombros de Ea (Enki na Suméria), tutelando as águas subterrâneas e a sabedoria. A figura armada com um arco, à esquerda, não foi definitivamente identificada mas pode ser Nusku. Segundo E. C. Krupp, este cilindro pode representar a celebração do novo ano, akitu, lit. "a cabeça do ano" (Período Acadiano, 2300-2200 a.C.; Museu Britânico)

O sistema possui desde cedo, como vimos, uma clara estrutura matemática que o tornou eficiente. Os povos da Mesopotâmia haviam adoptado um sistema numérico sexagesimal, perpetuado na divisão do círculo em 360º e nas horas e minutos que ainda hoje gerem o nosso quotidiano. O terceiro sistema de referência, oriundo do Egipto, foi a divisão em "Decanos" (associados a um período de dez dias, mais tarde plasmado na estrutura zodiacal através da divisão de cada signo em sectores de 10º). Outros contributos desta civilização decorrem da divisão (adoptada pelos Gregos) do seu calendário civil em 365 dias e ainda do dia em períodos diurno e nocturno, de 12 horas cada. [O ano egípcio de 365 dias tornou-se referência astronómica pela facilitação que proporciona em termos de cálculo. Neugebauer refere como, por exemplo, seria problemático calcular o número de dias entre o primeiro dia de dois anos gregos ou babilónicos afastados, digamos, 50 anos. No Egipto bastava multiplicar 365 por 50! (The Exact Sciences in Antiquity, Dover Publications, 1969, p.81)]

Com o passar do tempo, a Astrologia vai aglutinar os três sistemas com origem independente. Mas a "narrativa" do percurso do Sol através do Zodíaco será a mais importante.

Doze signos do céu o Sol percorre,
e, renovando o curso, nasce e morre
nos horizontes do que contemplamos
tudo em nós e o ponto de onde estamos.

Ficções da nossa mesma consciência
f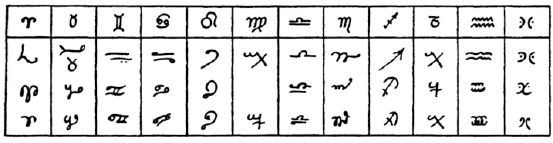azemos o instinto e a ciência,
e o Sol, parado, nunca percorreu
os doze signos que há no céu.

Nos horóscopos gregos mais antigos grafam-se os nomes mas não surgem símbolos, excepto, eventualmente, para os dois luminares. No período bizantino já encontramos símbolos para os planetas e signos zodiacais (na figura acima, exemplos encontrados em manuscritos bizantinos mais tardios, segundo Neugebauer e van Hoesen, Greek Horoscopes, Fig. 1).

Os símbolos dos signos zodiacais surgiram na Idade Média. Na tabela, exemplos provenientes de alguns manuscritos astronómicos tardo-medievais e renascentistas (Evans, J., The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p.104)

Equivalência entre as 12 Tribos de Israel (cujo acampamento é descrito em Nm. II) e os 12 signos zodiacais, segundo a exegese do teólogo Ethelbert W. Bullinger (The Witness of the Stars, Grand Rapids (Michigan): Kregel Publications, 1967 [London: 1893], p.18)

"Da Ordem dos ceos" (Livro intitulado Apprendis Curiozo: trata alguns principios da ordem & movimento dos ceos, & lugar dos elementos, & divizão da Terra; ”Recupillado por Sebastião Sardinha de Araujo”, 1612. [BNP, cota il-227], fl.4)

O modelo geocêntrico era "óbvio", respondendo a uma lógica experiencial e assimilando os conceitos filosóficos de perfeição e harmonia tão caros aos pensadores clássicos. Havia uma indiscutível beleza, mesura e hierarquia. Quanto à estrutura, escala e "sentido do maravilhoso" que imprime, poucos o conseguiram traduzir como C. S. Lewis:

"You must go out on a starry night and walk about for half an hour trying to see the sky in terms of the old cosmology. Remember that you now have an absolute Up and Down. The Earth is really the centre, really the lowest place; movement to it from whatever direction is downward movement. As a modern, you located the stars at a great distance. For distance you must now substitute that very special, and far less abstract, sort of distance which we call height; height, which speaks immediately to our muscles and nerves. The Medieval Model is vertiginous. And the fact that the height of the stars in the medieval astronomy is very small compared with their distance in the modern, will turn out not to have the kind of importance you anticipated. For thought and imagination, ten million miles and a thousand million are much the same. Both can be conceived (that is, we can do sums with both) and neither can be imagined; and the more imagination we have the better we shall know this. The really important difference is that the medieval universe, while unimaginably large, was also unambiguously finite. And one unexpected result of this is to make the smallness of Earth more vividly felt. In our universe she is small, no doubt; but so are the galaxies, so is everything - and so what? But in theirs there was an absolute standard of comparison. The furthest sphere, Dante's maggior corpo is, quite simply and finally, the largest object in existence. The word 'small' as applied to Earth thus takes on a far more absolute significance. Again, because the medieval universe is finite, it has a shape, the perfect spherical shape, containing within itself an ordered variety. Hence to look out on the night sky with modern eyes is like looking out over a sea that fades away into mist, or looking about one in a trackless forest-trees forever and no horizon. To look up at the towering medieval universe is much more like looking at a great building. The 'space' of modern astronomy may arouse terror, or bewilderment or vague reverie; the spheres of the old present us with an object in which the mind can rest, overwhelming in its greatness but satisfying in its harmony. That is the sense in which our universe is romantic [i.e. ilimitado, de algum modo caótico, "convulsivo", referência ao Romantismo, movimento estético e filosófico], and theirs was classical." (The Discarded Image, Cambridge University Press, 1964, pp.98-9)

Este universo fechado e sólido "estilhaçou" e, em seu lugar, surgirá o "Espaço", somente descrito de modo abstracto e matemático. Cada vez mais escuro, sem limites, indeterminado. (v. pág. Cosmologia)

A Astronomia desenvolveu-se, como vimos, a partir da amálgama das observações e procedimentos dos efemeridistas mesopotâmicos com o espírito da filosofia natural e geometria, apanágio da mundividência helénica. O nosso conhecimento da primitiva astronomia grega, anterior ao séc. IV a.C., resume-se a escassos fragmentos e aos comentários de Aristóteles acerca de (supostas) opiniões e concepções anteriores, que geralmente vai criticar. Mas tudo indica que se nutre uma concepção naturalista do Kósmos, explicando os fenómenos a partir das propriedades de certos elementos universais e de princípios reguladores inerentes ao mundo natural: phýsis.

Os gregos foram dogmáticos relativamente à utilização exclusiva dos movimentos circulares. Simplicius, no seu comentário ao de Caelo (Simplicii in Aristotelis de Caelo Commentaria) diz-nos que Sosígenes afirmara que este" princípio" se devia a Platão. Geminus (Isagoge, cap.I), afirmou que recuava aos pitagóricos. Estes, provavelmente por razões teológicas, simbólicas e estéticas, conceberam a Terra como uma esfera, em torno da qual os astros revolucionavam em movimentos circulares uniformes e perfeitos. Os predicados fundamentais dessa cosmologia serão bem acolhidos. Na República de Platão encontramos incidentalmente (no Mito de Er, o Arménio que morreu em combate mas voltou como "mensageiro das coisas do "Além"), uma descrição da estrutura axial do universo e do "Fuso da Necessidade" [a Necessidade, personificada por Ananke, era noção pitagórica], por cuja acção giravam as esferas. Na introdução de 1972 à sua tradução da obra sob chancela da Gulbenkian, Maria Helena da Rocha Pereira resume (XLI-XLII):

"A segunda cena contém o quadro da estrutura do universo, com a grande luz "direita como uma coluna, muito semelhante ao arco-íris, mas mais brilhante e mais pura" (616b), que segura a esfera em movimento. Das suas extremidades, pendia o fuso da Necessidade, cuja complexa estrutura é descrita quanto à forma e à cor, em termos tais que nos permitem adivinhar neles a correspondência com o Sol a Lua, os cinco planetas então conhecidos e as "estrelas fixas". O fuso repousa nos joelhos da Necessidade, e, no cimo do rebordo circular de cada um dos seus contrapesos, uma Sereia, girando com ele, emite uma nota musical. Do acorde dessas oito notas resulta a "harmonia das esferas". Além dessas figuras femininas, estão lá também as três Parcas ou Moirai, que cantam o passado (Láquesis), o presente (Cloto) e o futuro (Átropos), fazendo girar o fuso." O mito, cujo enquadramento é ético, contribuirá, segundo Rocha Pereira, para a "fixação de uma escatologia com castigos e recompensas, de acordo com o procedimento moral de cada um", é traduzido a partir da pág. 484 (9ª ed.; Fundação Calouste Gulbenkian).

Relacionada com o símbolo do "axis-mundi", é comum a comparação do movimento diurno, circular e uniforme do céu em torno do pólo ao funcionamento de um moinho. Surge em Cleomedes (séc. I a.C.) e em muitas mitologias (prioritariamente em culturas que habitavam regiões boreais, pelos exemplos aduzidos). Encontra-se, por exemplo, entre os Ostyaks da Sibéria. No Kalevala (colectânea de narrativas tradicionais finlandesas), o sampo, objecto mágico difícil de definir mas que pode ser um pilar, uma árvore ou um moinho, suporta-se em três "esteios" ou raízes, como a célebre Yggdrasill, a "Árvore (i.e. "eixo") do Mundo" da tradição nórdica: uma raíz sobe para o céu, outra finca-se na terra e uma terceira num redemoínho, provável representação do inframundo. As Eddas nórdicas também parecem comparar a rotação do eixo celeste - ou o deus incumbente - a um moinho. A dedução, segundo Krupp, respalda-se na etimologia do nome Mundilfari, o progenitor do Sol e da Lua. (E. C., Beyond the Blue Horizon..., Oxford University Press, 1992, p.297 et seq.)

Mais preocupado com a "mecânica" concreta e baseado na esferas de Eudoxus e na antiga teoria dos Elementos, Aristóteles gizará um sistema cosmológico elaborado e minucioso que se revelará duradouro. Este filósofo concebeu um universo finito e esférico, centrado numa Terra estacionária.

N'A Astronomia de Os Lusíadas (publicada em 1913-15, reeditada pela Junta de Investigações do Ultramar, Lisboa, 1972), Luciano Pereira da Silva (p.83, n.1) traduz um excerto de Pierre Duhem que resume o essencial da perspectiva aristotélica, começando com a axiomática distinção entre movimentos 'naturais': o circular dos corpos celestes e o rectilíneo dos terrestres (Le système du Monde, t. II, Paris, 1914, pp. 61 e 62):

"O sistema do Mundo concebido por Aristóteles estabelece uma profunda distinção entre os Céus, região de ordem imutável e do movimento circular, e o espaço inferior à esfera da Lua, região da mutabilidade e do movimento rectilíneo. Esta segunda região é ocupada pelos quatro elementos, dos quais a Terra ocupa o lugar mais próximo do centro, seguindo-se a água, depois o ar e por cima o fogo, não havendo, porém, limites definidos a separar os elementos. Tudo o que fica adentro do orbe lunar está sujeito à geração e corrupção. Acima deste orbe ficam as esferas celestes, feitas de éter ou quinta-essência, substância cristalina imutável, incorruptível, distinta dos quatro elementos. Ora Aristóteles distingue três espécies de movimento: o rectilíneo, o circular e o misto, composto dos dois primeiros. A cada substância simples corresponde um só movimento natural, que deve ser também simples, portanto um movimento de pura translação, o rectilíneo, segundo a vertical, ou um puro movimento de rotação em volta da Terra, o que ele chama circular. Este último, único que pode efectuar-se eternamente no mesmo sentido, convém, por natureza, ao éter, substância celeste. O movimento rectilíneo é o natural aos corpos corruptíveis e geráveis; ele não pode prosseguir eternamente no mesmo sentido porque o Universo é finito e nenhum móvel pode ultrapassar os seus limites. As translações simples, sempre executadas na direcção vertical, são de duas espécies: centrípetas, de cima para baixo, e este é o movimento natural dos corpos graves; ou centrífugas, de baixo para cima, e este é o movimento natural dos corpos leves. O corpo mais leve, o fogo, subirá verticalmente até ao orbe etéreo da Lua, inultrapassável. O corpo mais pesado, a Terra, descerá até ao centro do Mundo, não podendo prosseguir além, pois começaria nesse ponto uma ascensão contrária à sua natureza. Se um corpo grave sobe, ou um leve desce, é porque sobre ele actua um motor estranho e o seu movimento deixa de ser natural para ser violento. Do mesmo modo, só por violência um corpo sublunar segue uma trajectória diferente da vertical. Os astros, tanto fixos como errantes, são transportados em esferas homocêntricas segundo o sistema de Eudóxio, adoptado pelo Estagirita, e assim se movem todos em esferas cujo centro é o da Terra, guardando sempre a mesma distância relativamente a ela. Não sofrem, pois, deslocamento no sentido vertical, executando um movimento circular simples, uma pura rotação, sem translação alguma, centrípeta ou centrífuga. Quando, com Hiparco e Ptolomeu, se fizeram mover os planetas em esferas excêntricas, clamaram os adeptos da Filosofia de Aristóteles que tal doutrina era contrária à teoria peripatética dos movimentos naturais. Um planeta, descrevendo um círculo excêntrico, ora se afasta da Terra até o apogeu, ora se aproxima até o perigeu. Assim, andando os astros errantes em volta da Terra a distâncias variáveis, o seu movimento não seria circular simples no sentido aristotélico, mas composto de circular e rectilíneo, ora centrífugo ora centrípeto."

As principais opiniões dissonantes relativamente a este sistema geométrico, geoestacionário e hierarquizado foram (supostamente) as de Heráclides Ponticus (i.e. do Ponto Euxino, o actual Mar Negro) e Aristarco de Samos.

Voltando ao percurso dos modelos pretéritos, o engenhoso sistema de esferas homocêntricas de Eudoxus constitui, provavelmente, a primeira tentativa de explicação mecânica do Universo. [Salvaguarda-se que seguimos uma "reconstrução" académica commumente aceite mas baseada em fontes indirectas].

Assim, cada planeta estava fixado numa esfera que tinha liberdade para girar. Cada esfera com seu planeta estava ligada pelos pólos a uma esfera secundária exterior concêntrica que girava sobre um eixo diferente. Deste modo, cada esfera planetária estava ligada a outras, digamos, "não planetárias", ou "sem estrelas" seguindo a antiga expressão de Teofrasto [romaniz. Theóphrastos] (cit. por Dreyer, 1953, p.90). As esferas possuiam movimento uniforme. Cada planeta estaria incrustado no equador da sua esfera. os pólos da esfera estaria fixados na próxima, e assim sucessivamente (sistema recorria a 3 ou 4 esferas, o menor número no caso dos luminares). J. L. E. Dreyer, no cap. IV do seu clássico reeditado como A History of Astronomy from Thales to Kepler (Dover, 1953) descreve o modelo baseado nos estudos de autores pretéritos como Ideler e, principalmente, G. Schiaparelli:

"Every celestial body was supposed to be situated on the equator of a sphere which revolves with uniform speed round its two poles. In order to explain the stations and arcs of retrogression of the planets, as well as their motion in latitude, Eudoxus assumed that the poles of a planetary sphere are not immovable but are carried by a larger sphere, concentric with the first one, which rotates with a different speed round two poles different from those of the first one. As this was not sufficient to represent the phenomena, Eudoxus placed the poles of the second sphere on a third, concentric to and larger than the two first ones and moving round separate poles with a speed peculiar to itself. (...) The third sphere had its poles situated at two opposite points of the zodiac (on the second sphere), and rotated round them in a period equal to the synodic period of the planet, or the interval between two successive oppositions or conjunctions with the sun. These poles were different for the different planets, but Mercury and Venus had the same poles. (...) On the surface of the third sphere the poles of the fourth were fixed, the axis of the latter having a constant inclination, different for each planet, to the axis of the third sphere. Round the axis of the fourth sphere the rotation of the latter took place in the same period, but in a direction opposite to that of the third sphere. On the equator of the fourth sphere the planet is fixed, and it is thus endowed with four motions, a daily one, the orbital one along the zodiac, and two others in the synodic period." (pp.90-6)

Como Michael Hoskin explica (The History of Astronomy, Op. cit., 2003), os ângulos dos eixos e as velocidades de rotação eram escolhidos de modo a acautelar um resultado "fidedigno", sendo a esfera exterior a responsável pelo movimento diurno (a rotação aparente do céu em 24 horas). Os planetas, em que se observava retrogradação, apresentavam uma pequena diferença na inclinação dos eixos de duas das esferas, determinando um movimento numa linha que faria a figura de um "oito" (v. infra) e permitia ao conjunto das quatro esferas gerar o movimento "para trás" observável no céu (i.e., os laços da hipópede respondiam às alterações nos movimentos, às paragens e à alternância dos movimentos directos e das retrogradações).

Os padrões que configuravam o movimento da Lua no sistema de Eudoxus. A Lua imaginava-se fixada no Equador da esfera interior (Hoskin, The History of Astronomy, Op. cit., 2003)

O sistema era somente uma tradução aproximada, gerando movimentos rigorosamente regulares quando na realidade se observam complexidades ("inequalidades") e, ao obrigar a uma distância inalterável relativamente ao centro (Terra), não acautelava a presumida alteração das distâncias dos planetas (que as alterações do brilho denunciavam). A inflexibilidade e as diferenças entre a "simulação" e os fenómenos determinaram a optimização e, mais tarde, a criação de novos modelos. O sistema era compaginável com a descrição e princípios aristotélicos. Os movimentos são transmitidos do exterior para o interior do sistema, e são cumulativos. Para "cancelar" os movimentos combinados é necessário interpor esferas que os compensem (que actuem no sentido oposto), expediente que Aristóteles utilizará. Tendo em vista acautelar os fenómenos e manter-se fiel aos pressupostos da sua Física, Aristóteles chegará, no seu próprio sistema que estende e amplia o anterior (já optimizado por Cálipo ou Callipus), a considerar, no seu máximo, a existência de 55 esferas (Metafísica XII.8). N.B. este número é sempre polémico e sujeito a revisões em cada nova tradução ou interpretação, mas serão sempre muitas esferas!

Os aristotélicos posteriores recusaram isolar a discussão do movimento dos astros da respectiva natureza física. Como Edward Grant explica, a cosmologia aristotélica, muito mais tarde reforçada pelas ideias do seu comentador Averróis (ibn Rushd, 1126-1198), exigia que qualquer orbe celeste tivesse um corpo físico situado no seu centro. Os averroístas descartaram os modelos ptolomaicos como "ficções" somente úteis nos cálculos das posições. Adoptaram um sistema alternativo que era uma modificação das esferas homocêntricas de Eudoxus (vide Katherine Tredwell: Latin Astronomy, in Glick, T., Livesey, S. and Wallis, F., Op. cit. p.68). Num sistema no qual todos os orbes físicos eram concêntricos, a Terra preenchia uma função essencial. Aristóteles afirmou a existência de esferas transparentes e invisíveis às quais os corpos celestes estavam fixados ou por elas eram "alojados". Na opinião corrente, estes corpos (e.g., estrelas, planetas) eram observáveis porque, apesar de constituídos pelo mesmo 'éter' transparente, este era aqui muito mais concentrado, capaz de receber luz e tornar-se autonomamente luminoso ou, para os autores que consideravam os corpos celestes opacos, de reflectirem a luz do Sol (o lucido Planeta de Camões). Considerava-se ser a explicação mais acertada, apesar de uma opinião alternativa que considerava os corpos celestes capazes de serem tenuamente luminosos.Todavia, no que diz respeito aos movimentos e brilho, a realidade das observações astronómicas tornou insustentável a defesa deste sistema efectivamente concêntrico. As irregularidades e a observação de variações na luminosidade dos planetas tornaram claro que as suas distâncias à Terra sofriam variações. Daqui resultava que a Terra não poderia ser o centro físico das respectivas órbitas. A Astronomia concêntrica de Aristóteles foi substituída pelo sistema ptolomaico dos orbes excêntricos no qual a Terra, apesar de continuar estacionária e no centro do Mundo, não é mais o centro dos movimentos planetários. (Grant, E., "Cosmology", in: Lindberg, D. and Shank, M. (eds.), The Cambridge History of Science, Vol 2, 2013, pp.442-3).

Modelo explicativo do movimento de um planeta, segundo Eudoxus. A esfera 1 produz o movimento diurno para oeste; da esfera 2 resulta o movimento para leste ao longo da Eclíptica; as esferas 3 e 4 são responsáveis pelos movimentos de recuo e avanço necessários para acomodar a retrogradação do planeta (quando o astro inverte e depois retoma a direcção do seu movimento, fazendo as chamadas "laçadas" (Evans, James, The History and Practice of Ancient Astronomy, Oxford University Press, 1998, fig.7.11)

Segundo J. D. North, "...The collection of spheres governing a particular planet’s motion (say the four for Jupiter) will, quite apart from their own motions, be carried round inside the collection of spheres for the planet next above (in this case Saturn), and will thus share in that planet’s motions. To obviate this difficulty, and for other purposes, Aristotle added extra spheres. (Thus he needed three simply to neutralize the motion of all but the outermost sphere of Saturn, this outermost sphere being needed to account for the daily rotation of the sky.). By the time he had finished, he had a system with 55 homocentric spheres. These subtleties had been virtually forgotten (...), [because] planetary motions could be accounted for in the Ptolemaic manner in ways far superior to those devised by Eudoxus, Callippus, and Aristotle," (Chaucer's Universe, Op. cit., p.20) Os expedientes destes últimos traduziam-se numa colecção de esferas na qual o conjunto responsável pelos movimentos de um determinado planeta era, por sua vez, "arrastado" pelos aparatos dos planetas seguintes (exteriores). Para obviar este e outros problemas, Aristóteles acrescentou mais esferas (precisou, por exemplo, de três esferas suplementares somente para neutralizar a mencionada interferência ou arrastamento pelo planeta seguinte, excepto para o último, Saturno, pois era necessário acautelar o movimento diurno do conjunto). O modelo ptolomaico será o prevalecente, pela sua (relativa) eficiência e superior precisão, através do recurso aos expedientes que abordaremos de seguida.

"With centric and eccentric scribbled o’er,
Cycle and epicycle, orb in orb."
(Milton, Paradise Lost. Book VIII)

"...those monstrous orbs of Eccentricks, and those wandering in eccentric epicycles; which howsoever Ptolemy, Alhasen, Vitellio, Purbachius, Maginus, Clavius, & many of their associates, stiffly maintain to be real orbs, eccentrick, concentrick, circles aequant, &c. are absurd and ridiculous. For who is so mad to think that there should be so many circles, like subordinate wheels in a clock, all impenetrable and hard, as they feign, add & subtract at their pleasure."
(Robert Burton [1577-1640], The Anatomy of Melancholy [ed. Floyd Dell and P. Jordan-Smyth, New York: Tudor Publishing Co., 1938 (1927)], p.421)

A combinação excêntrico-epiciclo surgiu no período que medeia entre Cálipo de Cízico (c. 330 a.C., optimizador do sistema de Eudoxus) e Apolónio de Perga (c. 200 a.C.). A formulação matemática do sistema, que substitui as simples (e insuficientes) esferas de Eudoxus e Aristóteles na simulação dos movimentos dos luminares e dos planetas, recua, na opinião de Ptolomeu, ao segundo (Mourão, Ronaldo R. de Freitas, Dicionário Enciclopédico de Astronomia e Astronáutica, Rio de Janeiro, Ed. Nova Fronteira S.A., 1995, 45; vide Almagesto 12.1).

As duas hipóteses (excêntricos e epiciclos). No modelo epicíclico, o centro C move-se uniformemente em torno do observador O, enquanto o ponto M se move na mesma medida mas na direcção contrária em torno do ponto C. Logo, CM mantém uma direcção fixa. No modelo excêntrico, M move-se uniformemente em torno de D, centro esse que está a uma determinada distância do observador O. Estabelecendo que OD equivale ao raio do epiciclo (CM), verifica-se a equivaência dos dois modelos, que decorre da comutatividade da adição dos vectores, i.e. OD + DM = OC + CM, ou da constatação de que ODMC é um paralelogramo (quadrilátero cujos lados opostos são iguais e paralelos). Ou seja, as hipóteses eram indistintas no que diz respeito à explicação dos movimentos planetários.(Goldstein, Bernard R., Theory and Observation in Medieval Astronomy, Isis 63. Washington, D.C., 1972, Fig.1)

A ordem dos planetas era convencional: "Now in ancient astronomy the order of the planets is more or less a convention, without any sure foundation upon observable facts. Thus Ptolemy reminds us that there is no perceptible parallax in any of the planets, and that one has never observed a passage of Venus or Mercury before the disc of the Sun." (Pedersen, Olaf, A Survey of the Almagest (With Annotation and New Commentary by Alexander Jones), Springer, 2011, p.295).

A ordem dos planetas na antiga Mesopotâmia não estava obviamente relacionada com as distâncias, pois não existiam os conceitos de órbita ou de geometria de um "sistema". Uma destas primeiras sequências (Júpiter, Vénus, Saturno, Mercúrio, Marte) perpetuou-se na astrologia Helenística e está na origem da ordem "Caldaica" de uma das chamadas dignidades: os 'Termos' (como foi inicialmente constatado por Franz Boll). As variantes gregas já presumem a espacialidade e distância, mesmo que indeterminável. Apesar de pequenas complexidades com os planetas interiores, a ordem que prevaleceu (Saturno, Júpiter, Marte, Sol, Vénus, Mercúrio, Lua [de "fora" para "dentro"]) estava relacionada com as velocidades dos planetas em relação ao plano de fundo das estrelas. Apesar de não ser possível conhecer a distância e ordem dos planetas ainda por muito tempo, esta ordenação será tomada como definitiva, "pelo menos desde a época de Cícero" (J. D. North, Chaucer's Univerese, 1988, p.29). Encontramos um reflexo desta sequência nas horas planetárias e, a partir destas, nos nomes dos dias da semana em muitos idiomas.

Segundo Goldstein (Theory and Observation in Medieval Astronomy, Isis 63. Washington, D.C., 1972, p.41): "With rare exceptions medieval astronomers supported the nesting principle, but they considered the order of the planetary spheres to be an open question. There were three views: Mercury and Venus both lie beneath the sun; Mercury is below the sun and Venus above it; Mercury and Venus both lie above the sun.". Como Ptolomeu havia afirmado, somente observando um trânsito teríamos uma prova conclusiva. Mas nunca tinha observado e sugeriu que talvez nem fosse possível devido à pequena dimensão angular. Prevalecia uma teoria de que as órbitas se encaixavam, a partir de estimativas e conjecturas muito incertas de algumas distâncias.

A preocupação com a ordem dos planetas levou à consideração das suas distâncias. As distâncias de Ptolomeu (nas Hipóteses Planetárias) foram gizadas a partir das distâncias da Lua e do Sol (que supostamente "conseguira" determinar) e assumindo proporções relativas para os restantes planetas (pois onde terminava o aparato geométrico de um. começava o do imediato). Na realidade, desde Hiparco que através da paralaxe se podia ter uma estimativa razoável das distâncias (maior e menor) da Lua. Em relação ao Sol não foi possível. Aristarco estava correcto em tese mas a agilização não era exequível e seu o resultado estava afastadíssimo da realidade. Somente após Edmond Halley e a observação dos trânsitos de Vénus (apesar do efeito óptico "black drop" que dificulta a medição) se conseguiu chegar a uma distância (média) minimamente fiável. Voltando ao método geométrico e apriorístico de Ptolomeu, a maior distância da Lua permitia-lhe (supostamente) conhecer as distâncias (em raios terrestres) de Mercúrio e Vénus, a do Sol conhecer a dos restantes planetas e a da esfera das "estrelas fixas". Eram calculadas sempre em raios terrestres, utilizando: o raio do deferente do planeta (R), o raio do epiciclo (r), a excentricidade (e). Assim, para Vénus, Marte, Júpiter e Saturno, a maior distância relativa era D = R + (r + e); a menor d = R - (r + e). Mercúrio era um caso diferente e mais complexo (vide exposição e desenvolvimento em Goldstein, Bernard, and Swerdlow, Noel, Planetary Distances and Sizes in an Anonymous Arabic Treatise Preserved in Bodleian Ms. Marsh 621, Centaurus 15. Copenhagen, 1970-71, p.136).

Muitos astrónomos medievais viam estas distâncias como somente provisionais, e surgiram diversos cálculos alternativos. Mas os valores nesses textos mais tardios situam-se, geralmente próximos dos de Ptolomeu, colocando a esfera das estrelas fixas (o limite do Universo) a 20000 raios terrestres. Toda esta abordagem deve ser contextualizada na estrutura teórica que a determinou. A variação de tamanho dos planetas, que ficou por abordar convenientemente por Ptolomeu, também era assiduamente discutida na Idade Média. Bem como outras consequências (ou "inconsequências") das teorias planetárias. Vénus, segundo a teoria, deveria mostrar fases. Como estas não eram observadas (só após a utilização do telescópio por Galileu foi possível), Al-Bitruji (o "Alpetragius" latino) resolveu a dificuldade afirmando que os planetas teriam luz própria! (Golstein, Theory and Observation..., p.45).

Para compreender os desenvolvimentos da astronomia grega e os modelos geométricos definitivamente gizados, pode ser útil partir da Teoria Solar de Ptolomeu, i.e. explicação dos fenómenos relacionados com os movimentos específicos do Sol. Daqui se pode extrapolar para as outras aplicações. Seguimos a exposição de James Evans (1998: p.205 et seq.). Depois, outro exemplo ptolomaico usado para a determinação das longitudes de alguns dos planetas (ibid., pp.355-6).

Assim, todas as mudanças relevantes (estações do ano, alteração no número de horas diurnas e nocturnas, direcções do orto e do ocaso do Sol, comprimento da sombra ao meio-dia) podiam ser explicadas através de um modelo no qual o Sol percorria um círculo (a Eclíptica) inclinado em relação ao Equador. Mas havia uma anomalia: a dimensão variável das estações do ano. A medição precisa da duração do ano ("Vera anni quantitas" em Latim) era relativamente fácil recorrendo aos equinócios (os solstícios são, pela sua natureza, fenómenos mais difíceis de precisar). O equinócio podia ser aproximadamente determinado medindo, para começar, a altura do Sol ao meio-dia nos dias dos solstícios. A altura do Sol no dia do equinócio deveria situar-se exactamente a meio desses valores. Media-se a altura meridiana do Sol em dias sucessivos em redor da data esperada do equinócio e interpolava-se para determinar o momento exacto. Como a declinação do Sol muda rapidamente nesta altura do ano, era possível determinar o momento do equinócio com razoável aproximação (uma modesta fracção do dia). Dos diversos instrumentos à disposição, o quadrante colocado no plano do meridiano era o mais preciso na medição das alturas. Ptolomeu descreveu no Almagesto (I, 12) duas versões do instrumento. Também podia, e foi decerto num passado remoto, inferida a partir do nascimento helíaco de uma ou mais estrelas.

O fenómeno da desigualdade das estações do ano é conhecido pelo menos desde Cálipo (Κάλλιππος) e os valores de Hiparco (120 a.C.) são uma referência fiável. Demais, o tamanho das estações altera-se com a passagem dos séculos; têm actualmente (sequencialmente e começando na Primavera): 93, 93, 90 e 89 dias. Hiparco elencou (circa 130 a.C.): 94 1/2, 92 1/2, 88 1/8 e 90 1/8 dias. Descobriu-se assim uma "anomalia solar" que comprovava que o movimento (aparente) do Sol não tinha a mesma velocidade angular em todos os pontos da sua órbita. Assim, os antigos astrónomos gregos precisaram abandonar a sua versão simplista circular e uniforme, com a Terra no exacto centro (esquema 1, infra), inventando modelos que respondessem ao desafio. [Hoje sabemos que as premissas eram falsas e que é a Terra que orbita o Sol segundo uma elipse]. Todavia, procurou-se ajustar o modelo perpetuando princípios físicos aristotélicos. Com um "pequeno" ajustamento, manteve-se o movimento circular e a velocidade uniforme.

Esquemas da teoria solar recolhidos em Evans: 1998: pp.210-12. Numerados por nós e explicados no texto. Convém acrescentar a seguinte legenda: VE (Equinócio Vernal), AE (Equinócio de Outono), SS (Solstício de Verão) , WS (Solstício de Inverno); imagine-se o observador no pólo norte da Eclíptica. No esquema 1, a Terra ("Earth") está no centro.

Hiparco assumiu (simplesmente) um centro deslocado da posição original (i.e. não coincidente com a Terra). O círculo da órbita solar passou a ser excêntrico. O esquema 2 explica a variação das dimensões sazonais para a nossa época (C é o centro do excêntrico do Sol, O é a Terra; a linha que os une permite encontrar o apogeu A e o perigeu Π (Pi), o ponto da órbita mais afastado e mais próximo da Terra, respectivamente). O segmento entre A e Π é a chamada "linha de ápsides" (que une os pontos extremos da órbita: apogeu e perigeu). O ângulo A é a longitude do apogeu; OC / CA = excentricidade. Neste modelo, o Sol viaja a uma velocidade constante (em relação a C) mas parece, a partir da Terra, mover-se mais rapidamente nas imediações do perigeu e mais devagar no apogeu, devido às diferentes distâncias a que está do nosso planeta.

Outro modelo, gizado praticamente em paralelo, permite obter exactamente o mesmo resultado. Utiliza um deferente que "carrega" ou transporta um epiciclo ("pequeno círculo", cujo centro [a que podemos chamar o "planeta fictício"] se move sobre outro círculo). O conceito parece recuar a Apolónio de Perga, todavia (ainda) sem a componente quantitativa exigida, apenas a explicação física. No esquema 3, o Sol (S) movimenta-se no epiciclo enquanto o centro desse epiciclo (K) orbita (no sentido contrário ao dos ponteiros do relógio, retrógrado, como se observado do pólo norte da Eclíptica) o círculo deferente, que por sua vez está centrado na Terra (O). O ângulo α aumenta uniformemente com o tempo. Entretanto, o Sol (S) movimenta-se (peculiarmente) no sentido dos ponteiros do relógio no seu epiciclo. Logo, o ângulo β também aumenta uniformemente com o tempo. Evoluíndo ambos os movimentos com o mesmo progresso, teremos β = α. Ambos os movimentos se completam num ano (pois trata-se do Sol) e os ângulos α e β são sempre iguais. O movimento resultante da combinação de movimentos não é nada mais do que o movimento uniforme de um círculo excêntrico, como usado no modelo anterior. Porque α = β, o raio rotativo KS (no epiciclo) permanecerá sempre paralelo ao segmento OZ. Os modelos são matematicamente equivalentes. Seguindo a (moderna) propriedade comutativa da adição (dos vectores); OS = OK + KS. Noutra ordem OS = KS + OK. É o que se representa no último esquema (4), um modelo excêntrico; o ângulo α é chamado "anomalia média" (por definição: a conversão em ângulo do tempo desde que o astro passou pelo periastro, na sua órbita).

Epiciclo_deferente_equivalência (Bigourdan)

As teorias planetárias geralmente assumiam que o movimento do astro no epiciclo equivalia (na sua velocidade angular) ao do
centro do epiciclo sobre o deferente. Portanto, o planeta percorria o epiciclo completo no mesmo tempo que o centro desse epiciclo
percorria o círculo do deferente. Neste caso, demonstra-se que estes dois expedientes (epiciclo e deferente) se equivalem rigorosamente.
(G. Bigourdan, L'astronomie : évolution des idées et des méthodes, Paris: Ernest Flammarion, 1920 [1911], Fig. 29)

Os dois expedientes (excêntricos e epiciclos) serão ulteriormente combinados e adaptados na procura de respostas fiáveis para os fenómenos observados.

Teoria Planetária - longitudes (Ptolomeu)

Esquema da teoria definitiva das longitudes para Vénus e para os três restantes planetas superiores, segundo Ptolomeu. A Terra está representada pelo ponto O. C é o centro do círculo deferente mas o centro do epiciclo move-se com uma velocidade angular uniforme relativamente ao ponto E. (Evans, 1998, p.355)

O esquema acima descreve a teoria das longitudes que permitia determinar as posições dos planetas ao longo do círculo oblíquo (Eclíptica). Mercúrio não está incluído devido a uma complexidade extra. O círculo do deferente (A K Π) é excêntrico (por isso para Ptolomeu estas duas definições são intercambiáveis). Estrutura-se em torno do centro C. A Terra está representada em O. A linha entre O e C intesecta o deferente/excêntrico em A (apogeu do excêntrico) e Π (perigeu). É a chamada linha dos ápsides (que é também a linha de simetria das retrogradações do planeta). A linha OZ aponta para o Ponto Vernal (direcção referencial para a medição da longitude, v. símbolo à direita no esquema). O ângulo A representa a longitude do apogeu do excêntrico, que é diferente para cada planeta. O centro K do epiciclo move-se para Leste no deferente/excêntrico mas o seu movimento não é uniforme quando observado da Terra nem sequer do centro do deferente: somente é uniforme quando observado do de um 3º centro, o ponto aequans (E). Um hipotético observador aí colocado veria o planeta percorrer ângulos iguais em tempos iguais. Assim, devido a este ponto, Ptolomeu faz com o ponto K (centro do epiciclo) se movimente mais devagar no apogeu e mais depressa no perigeu, algo que, como James Evans comenta, contorce a física de Aristóteles. EX é paralela a OZ; EX é a referência (0º) para ângulos medidos a partir do aequans.

A longitude (λ) incrementa de modo uniforme, determinada pelo período tropical do planeta (duração média de que o planeta precisa para dar a volta ao Zodíaco, e.g., Marte aproximadamente em 2 anos, Júpiter em 12 anos, etc.). O planeta P percorre o epiciclo do mesmo modo que K o faz no excêntrico, no sentido contrário ao dos ponteiros do relógio, i.e. retrógrado (como se observado do pólo norte da eclíptica). A posição de P no epiciclo é especificada pelo ângulo μ, a "anomalia epicíclica média". O movimento uniforme de P deve ser medido em função da revolução uniforme da linha EK. μ incrementa uniformemente, dependendo do período sinódico de P. O raio CK do excêntrico é irrelevante, excepto na medida em que deve ser muito maior do que o raio da Terra, uma vez que os planetas têm paralaxes negligenciáveis (ou sejam estão muito longe).

Na teoria de Ptolomeu, CE = CO, portanto o ponto aequans e a Terra são equidistantes do centro do círculo deferente. O raio do epiciclo (r = KP) é fixo relativamente ao raio "R" do deferente (não designado na ilustração) e a razão r / R seria específica para cada planeta. A razão CO / R (ou CE / R) representava a excentricidade (e) do planeta, que também é específica de cada um para uma determinada época.

Esquema (anotado) da Teoria das estações e retrogradações (Purbachius. Theoricae novae planetarum (ed. Erhard Ratdolt, 1485; exemplar da bibliothèque Sainte-Geneviève (BSG), Paris)

Adoptaram-se diferentes soluções para os planetas interiores e para os planetas exteriores (como hoje os designamos):

"An inferior planet, Venus for example, moves uniformly around its epicycle at such a rate that it comes as close as possible to the earth once each synodic period. At the same time the center of her epicycle stays always in line with the sun, thus moving around its deferent once each year. By these devices Venus is constrained always to appear as a morning or evening object and to execute its cyclic variations of brightness once each synodic period, in agreement with the observed facts. A consequence of combining these motions is that Venus moves 360° around her epicycle once every 225 days, which is the so-called sidereal period of the planet. A superior planet moves in a way quite different from an inferior planet. Jupiter, for example, moves around his epicycle once each year, with the line joining planet and epicycle center always parallel to the earth-sun line. Simultaneously, Jupiter’s epicycle center moves round its deferent at a rate such that Jupiter will come closest to the earth once each synodic period. Combining these motions, Jupiter’s epicycle must roll 360° around its deferent once every 11.9 years, which is Jupiter’s sidereal period. These schemes, although placing the inferior and superior planets on different footings, ensure agreement with observation. First, it follows that each planet will appear in retrograde motion for a time every synodic period. Second, the sidereal period of a planet may be thought of as the long-run average time it takes for the planet to move once around the zodiac through the background stars, and here again the predictions of the Ptolemaic theory are in accord with the facts." (Wyatt, Principles of Astronomy, 1964, pp.150-51)

Portanto, Marte, Júpiter e Saturno moviam-se de modo a que a linha que unia o planeta ao centro do epiciclo era sempre paralela à que unia a Terra e o Sol; nos casos de Mercúrio e Vénus, os centros dos respectivos epiciclos situava na linha que unia a Terra e o Sol (estes planetas, como se observa, nunca se afastam muito. angularmente, do Sol). Repare-se que as latitudes estavam contempladas no modelo, inclinando o deferente em relação à eclíptica (valor dessa inclinação dependia do planeta em causa), contudo mantendo o epiciclo do planeta sempre paralelo ao plano da eclíptica. O desenho do modelo assegurou a contiguidade dos círculos dos planetas: o ponto mais afastado de um (apogeu) era contíguo ao perigeu do seguinte. O tamanho dos deferentes e epiciclos não era relevante mas sim a razão ou proporção entre os seus raios.

- Ligação para o vídeo "Epicyclical Theory" (Museo Galileo, narração em Inglês).

Representação do funcionamento básico do epiciclo de Marte, Júpiter ou Saturno. Representa-se a Terra (T), o deferente e o centro do epiciclo (C) que roda em torno da Terra no período que o planeta demora em torno do Zodíaco, a sua revolução sideral (e.g., Marte 687 dias, Júpiter 11.9 anos, Saturno 29.5 anos). O movimento no deferente é chamado "movimento em longitude", ao longo do epiciclo é chamado "anómalo". Quando o planeta chega ao ponto α, determinado como estando a 1/2 da distância αγ, as duas velocidades radiais equivaler-se-ão por um breve período e o planeta será visto da Terra (T) a parar, iniciando movimento retrógrado. Chegando a β, planeta volta a ficar estacionário e resume o movimento directo. A razão entre os raios dos dois círculos é ajustada de modo a fazer coincidir o modelo com a teoria, com os fenómenos. Quando o planeta está na posição p1 está mais perto da Terra e o prolongamento da linha CT, no sentido oposto (antes de T), passaria pelo Sol (não representado): planeta estaria em Oposição; quando o planeta está na posição p, mais afastado na Terra, estará em Conjunção (o Sol estaria entre T e p1). N.B. Para Mercúrio e Vénus a situação seria diferente: o deferente rodaria no período de 1 ano, a linha TC apontaria sempre na direcção do Sol, o movimento do planeta no epiciclo demoraria o período a que agora chamamos heliocêntrico, 88 dias para Mercúrio e 225 para Vénus. (fonte: Dreyer, J.L.E. Op cit., p.152)

No primeiro expediente, o planeta move-se uniformemente num círculo excêntrico (relativamente à posição da Terra). Pareceria deslocar-se mais depressa quando mais próximo e mais lentamente quando mais afastado. O segundo é, como vimos, o sistema de epiciclos e deferentes. Evidentemente, estes expedientes violavam os princípios filosóficos e cosmológicos mas respondiam ao problema posicional dos corpos celestes (aos fenómenos observados no céu). Por exemplo, o epiciclo percorrido pela Lua movia-se ao longo do deferente de maneira "uniforme", contudo uniforme em relação à Terra e não ao centro (do mencionado deferente). Trata-se portanto de um movimento que não é uniforme! Ptolomeu expandirá o modelo utilizando ainda outro expediente artificial e polémico: o aequans ("equante"). Trata-se de um ponto simétrico à posição da Terra (que já é, em si mesma, excêntrica). O planeta deverá doravante mover-se uniformemente relativamente a este ponto (que não está no centro). Para que isso aconteça, precisa verificar-se variação de velocidade na órbita planetária. Ou seja, o movimento de um planeta cuja velocidade é variável é observado no aequans como sendo (aparentemente) uniforme.

Tratou-se de um "truque" que simulou manter a premissa do movimento circular e uniforme. Assim era quando observado desse ponto fictício. Na realidade, os movimentos planetários observados da Terra não são uniformes (pois as órbitas são, como Kepler descobrirá, elípticas). Assim, Ptolomeu respondia aos fenómenos e o seu sistema, que era matemático, conseguia prever as posições com suficiente rigor. Isto não acontecia no modelo aristotélico que explicava o Universo na perspectiva da filosofia natural, todavia muito impreciso (mesmo "desastroso") na previsão dos fenómenos. Mais tarde, o prolífico Nasir al-Din al-Tusi (séc. XIII), no seu Tahrir al-Majisti ("Comentário ao Almagesto") proporá um dispositivo matemático no qual um pequeno círculo gira dentro de outro maior, permitindo evitar o recurso ao aequans.

No caso de Mercúrio Ptolomeu utilizou o expediente cinemático de um deferente móvel, cujo centro rodava num pequeno círculo (o circulus parvus, "circulo pequeno", dos astrónomos medievais) concêntrico com a Eclíptica. Como Peuerbach (Purbachius, Purbáquio) clarificou nas Theoricae novae planetarum ("Novas teorias dos planetas"), isto exige outro "centro" (para além dos três já utilizados, sc. o do "Mundo", o do deferente e o ponto aequans), em torno do qual o centro do deferente executa numa pequena revolução.

A "Teoria de Mercúrio" (detalhe) com o pequeno círculo percorrido pelo centro do deferente. Purbachius. Theoricae novae planetarum (ed. Erhard Ratdolt, 1485; exemplar da bibliothèque Sainte-Geneviève (BSG), Paris). Aqui o mesmo pequeno círculo ("Parvi Cir.") em volvelle cometida à determinação das posições de Mercúrio, no Astronomicum Caesareum (Ingolstadt, 1540) de Petrus Apianus (Peter Bennewitz).

Um dos conflitos da teorização Grega acerca dos movimentos planetários decorria, como se infere, da respeitada perspectiva aristotélica das esferas providas de movimento naturalmente circular e uniforme, também concêntricas com o centro da Terra, que seria o centro do Universo. Averróis (séc. XII) lamentará: "Na nossa época, a Astronomia não é acerca de algo real; a esfera que existe na nossa época é um modelo que se conforma com os cálculos, não com a realidade." (Tafsır Mã ba‘d al-tabı‘a XII c. 45).

Como se percebe, desde Apolónio e Hiparco que as anomalias observáveis nos movimentos dos planetas podiam ser quantitativamente geridas e explicadas com o recurso a círculos excêntricos e epiciclos, ou por uma combinação de ambos. O dilema que os astrónomos enfrentavam era, portando, acautelar a concentricidade sacrificando a uniformidade ou acautelar a uniformidade sacrificando a concentricidade (tanto os excêntricos como os epiciclos determinam que a distância dos planetas ao centro seja variável). Foram introduzidos para conseguir fazer corresponder as posições às longitudes correctas.

O ponto ptolomaico suplementar a que mais tarde se chamará aequans equivalia ao foco "vazio" da elipse muito mais tarde gizada por Kepler na sua explicação definitiva do movimento dos planetas. Conforme as duas primeiras Leis do astrónomo Alemão, a Terra movimenta-se mais rapidamente quando próxima do foco (ocupado pelo Sol) e mais lentamente quando na proximidade desse segundo foco, a partir do qual o movimento do planeta parece uniforme. Foi uma engenhosa aproximação ao fundamental princípio da conservação do momentum angular. Kepler publica as suas conclusões acerca das órbitas no importantíssimo Astronomia Nova (1609), culminando a sua longa investigação do movimento de Marte. Mas o Epitome astronomiae Copernicanae, de 1618, constitui a primeira exposição completa do Sistema Solar com as órbitas elípticas dos planetas correctamente descritas.

Expedientes orbitais geocentrismo (Hoskin, 2003)

Os diversos métodos utilizados para os movimentos dos planetas: Excêntrico, combinação Epiciclo-Deferente e, por fim, o ponto aequans ptolomaico. A introdução deste ponto é atribuída ao sábio alexandrino por alguns autores e divulgadores mas não há no Almagesto qualquer reclamação da autoria (vide Alexander Jones: Greco-Roman Astrology and Astronomy, in Jones, A. and Taub, L. (eds.), The Cambridge History of Science, Vol I, 2018, p.390). Constitui uma boa aproximação à 2ª Lei do Movimento de Kepler, uma vez que o planeta percorre áreas iguais do seu plano orbital em tempos iguais. Repare-se no sentido da rotação dos pontos; em baixo, a explicação "definitiva", que hoje conhecemos, para os fenómenos observados: as órbitas são, na realidade, elípticas (fonte das ilustrações: Hoskin, M., The History of Astronomy, Op. cit., 2003)

Em resumo; o modelo-padrão ptolomaico (“the ferris-wheel universe”, "o universo roda-gigante" como lhe chamou Arthur Koestler) foi estabelecido na época helenística. O Almagesto (Al Kitab al Mijisti, arabização de Hē Megalē Syntaxis, Magna Syntaxis em Latim) de Ptolomeu, autoridade por pelo menos catorze séculos, incluía um catálogo de estrelas, registava a determinação da Precessão, explicava técnicas de medição angular e os movimentos dos corpos celestes na visão geocêntrica do Universo. Uma órbita planetária é nele tipicamente representada por um círculo (epiciclo) cujo centro se situava num círculo maior (deferente) que era simultaneamente excêntrico. Acrescentaram-se expedientes para adaptar o modelo à realidade dos fenómenos e assim salvar ou preservar as aparências. Tratava-se, no fundo, de traduzir o desenho geométrico do Universo.

A excentricidade da posição da Terra "trai" os princípios aristotélicos mas explica com aproximação os fenómenos observados. E Ptolomeu mostrou que as irregularidades ainda verificadas podiam ser reproduzidas. Como Michael H. Shank refere, "Ptolomeu, no Almagesto, utiliza excêntricos e epiciclos para dar conta das posições e velocidades dos planetas e para a criação de tabelas que, por seu lado, tornam possível prever as posições. Epiciclos transportados por deferentes orbitando centros que não são coincidentes com o centro do Universo tornaram-se característicos da astronomia matemática da tradição grega. Nestes modelos de algum modo "descarnados" (geralmente vistos como arranjos de círculos em vez de esferas), as considerações cosmológicas e os princípios físicos foram preteridos relativamente ao objectivo primeiro: a previsão das posições." (Rings in a Fluid Heaven: The Equatorium-Driven Physical Astronomy of Guido de Marchia, Centaurus 2003: Vol. 45: p.176, [trad. nossa]). A visão espacial do Universo e o conceito de órbita têm origem grega. Mas é somente com Hiparco (gr. Ἵππαρχος; c.190 - c.120 a.C.), com enorme influência sobre Ptolomeu, que a astronomia grega passa de (apenas) descritiva a preditiva.

Acerca das tabelas

A informação tabulada assumiu um papel fundamental na prognose dos fenómenos: "As tabelas astronómicas são expedientes para transformar o tratamento de problemas complexos em aritmética elementar. Desde a Antiguidade que os astrónomos abordam muitos problemas através de tabelas; entre eles, destaca-se o tratamento dos movimentos dos planetas, bem como o dos movimentos do Sol e da Lua. Era comum atribuir aos planetas velocidades médias constantes para calcular as suas longitudes médias em qualquer momento passado ou futuro, acrescentando a essas longitudes médias correções, chamadas "equações", para determinar as suas verdadeiras longitudes." (Chabás & Goldstein, Computing Planetary Positions: User-Friendliness and the Alfonsine Corpus, Journal for the History of Astronomy 44 (2013), 257–276, 479–480). A astronomia medieval só muito excepcionalmente seria observacional, era rotineiramente uma astronomia de cálculo. E esses cálculos eram, quase exclusivamente, no sistema sexagesimal.

As tabelas de Ptolomeu, principalmente as tabulae manuales (Procheiroi Kanones, chamadas "handy tables" na literatura em Inglês), mais práticas e dotadas de comentários que vão sendo acrescentados à sucinta e insuficiente introdução disponível no original) são utilizadas pela minoria com maiores competências matemáticas. Paralelamente continuam a utilizar-se modelos aritméticos (cujas origens recuam à Mesopotâmia), e assim continuará a ser até ao final da Idade Média. O próprio Almagesto, compêndio sistemático, parece ter sido negligenciado pela maioria dos estudantes: "Conheciam-no pelo nome mas cultivavam a Astronomia a partir de textos secundários e abreviados" (Pedersen, O., [Jones, A., ed.], A Survey of the Almagest..., Springer, 2008 (1974), p.19). Ao contrário das modernas listagens diárias das posições planetárias (calculadas), as antigas tabelas disponibilizavam tábuas gerais a partir das quais era possível calcular (de modo mais ou menos oneroso) a posição de um planeta para qualquer data no passado ou no futuro. Serão gradualmente mais fáceis de utilizar, pre-calculando resultados para determinadas datas de referência (radices). Como Owen Gingerich explicou, "If we wish to calculate actual planetary positions from Ptolemy's epicyclic model, we need to have in hand the numbers that specify the actual geometry. We must know, for example, the size of the epicycle with respect to its circular deferent, the period of motion of the planet in the epicycle and of the epicycle along its deferent, and so on. Altogether there are seven such parameters, of which five are independent for each planet. Given these parameters and the geometry of the model, we can find the celestial longitude of a planet for any time, but in the days before pocket calculators this would have been rather hard work. Even with a small calculator the procedure is tedious enough to ruin a morning. So this is where astronomical tables come in. By precalculating certain fundamental parts of the planet's motion, the whole operation becomes much more manageable." (The Astronomy of Alfonso the Wise, in: The Great Copernicus Chase and other adventures in astronomical history, Sky Publishing Corp. and Cambridge University Press, 1992, p.59).

O funcionamento das tabelas alfonsinas medievais foi resumidamente descrito num artigo de Emmanuel Poulle, em colaboração com Owen Gingerich (Les positions des planètes au Moyen Âge: application du calcul électronique aux tables alphonsines, in: Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres, 1967, 111-4, 531-548; pp.538-39):

"Simplificando ao extremo, podemos afirmar que, a partir da teoria epicíclica exposta no Almagesto, o movimento de um planeta em longitude resulta de dois movimentos regulares, o do planeta sobre o seu epiciclo e o do centro do epiciclo [ponto fictício] em torno da Terra, sendo ambos corrigidos das suas inequalidades: a excentricidade do deferente (i.e. a distância do centro da Terra ao centro deste círculo) percorrido pelo centro do epiciclo a a adopção de um ponto diferente (i.e. deslocado) do centro para poder apreciar a regularidade do centro do epiciclo. O movimento regular do planeta no seu epiciclo é chamado "argumento médio", o do próprio epiciclo diz-se "movimento médio" [ideal ou nocional]. As duas correcções são chamadas "equações": equação do centro e equação do argumento. Estas, que configuram funções trigonométricas complexas, uma do movimento médio, a outra alternadamente do movimento médio, do médio argumento e da equação do centro. Convém insistir que as tabelas medievais não devolvem directamente as posições planetárias [como fazem as efemérides]; formam um conjunto de tábuas que permitem, atrvés de onerosos cálculos, determinar essas posições. São constituídas por duas partes, mais alguns elementos ancilares. Em primeiro lugar, existem tabelas que estabelecem facilmente, para qualquer data dada, os valores assumidos nessa mesma data pelos movimentos regulares variáveis do planeta: o movimento médio e o argumento médio; todavia não ambos, mas apenas um ou outro, visto que, na teoria ptolomaica, para cada planeta uma dessas duas coordenadas é estabelecida diretamente a partir do argumento médio do Sol. A segunda componente das tabelas consiste em grelhas que fornecem todos os elementos necessários para o cálculo das duas equações, uma por planeta. As tabelas alfonsinas ajustam-se a qualquer data, isto é, a todos os intervalos de tempo decorridos desde uma era escolhida como origem [radix], que são transformados num número de dias expresso em numeração sexagesimal. A partir daí, as tabelas de movimentos médios e argumentos médios, que tradicionalmente eram tabelas de variações diárias, mensais, anuais e plurianuais, ficam limitadas a tabelas de multiplicação (por sessenta) dos valores dos movimentos diários. Todas as tabelas astronómicas medievais fornecem "equações" somente para ângulos expressos em graus inteiros; para ângulos intermédios, cujo valor é expresso em minutos e segundos, é necessário interpolar entre dois valores próximos.As posições para cada planeta eram registadas em signos (s), graus, minutos, segundos e terços. Os nodos lunares apenas até aos minutos de arco." [Trad. nossa]

Como deve o historiador da ciência abordar a informação astronómica posicional que lhe chega do passado? E. Poulle & Owen Gingerich comprovaram desfasamentos não em relação às posições informáticas de Bryant Tuckerman (exportadas, como se sabe, na primeira metade anos 60 do séc. passado recorrendo a equipamentos da IBM e publicadas pela American Philosophical Society): "D'ores et déjà, on peut noter qu’il résulte, de la comparaison des positions alphonsines avec celles de Tuckerman, que les planètes supérieures sont mieux traitées que les planètes inférieures: l’écart varie environ de — 1° à + 2° pour Saturne et pour Jupiter, de — 10 20° à + 1020’ pour Mars, tandis qu'il est de — 3° 20’ à + 1° pour Vénus et surtout de — 6° à + 14° pour Mercure, décidément mal servi par une théorie pourtant plus complexe que celles de ses soeurs; pour la Lune, l’écart varie de — 2° 20’ à + 2°." (Les positions des planètes au Moyen Âge..., Op. cit., 1967, p.547).

Excerto de uma página das efemérides de B. Tuckerman: Planetary, Lunar, and Solar Positions A.D. 2 to A.D. 1649 at Five-Day and Ten-Day Intervals (Memoirs of the American Philosophical Society, vol. 59, 1964)

E se, como se constata, os lentos e ponderosos Júpiter e Saturno parecem (sem surpresa) obter resultados mais fiáveis, Tycho Brahe não deixou de escarnecer de uma "conjunção magna" cuja predição nas tabelas (alfonsinas) falhava por um mês completo: "...Saturni et Jovis magna conjunctione per integrum mensem aberraverit." (Opera omnia, T. I, 1913, p.40). O que para os astrólogos se revelaria "desastroso" no inerente juízo, porque o diferencial se traduziria num deslocamento de ~5º na posição zodiacal do importante fenómeno. Portanto, a determinação das posições astronómicas do passado, anterior ao séc. XVI, nutria-se de uma precisão "ilusória" respaldada nos modelos plasmados nas suas tabelas (com as suas aproximações a fracções de grau unicamente nocionais e que somente existiam no papel), enquanto a opção observacional se revelava ainda pífia: "Quels instruments d'observation, avant le XVI siècle, pouvaient offrir des résultats aussi remarquables, eux dont on est heureux de tirer une approximation du degré? Le fait que cette précision soit absolument illusoire, faute que les bases en aient été assurées, n'importe pas." (Poulle & Gingerich, Op.cit, p.538). Por tudo isto, os autores defenderam a óbvia necessidade do historiador [neste caso o medievalista] recorrer à informaçáo posicional coeva, possível e extraível na época (e dinamizaram um projecto informático respaldado nesses parâmetros). Portanto, a comparação directa com os resultados retrospectivos (segundo fórmulas actuais) radica num anacronismo: "(...) ces listes de positions souffrent, pour ce qui concerne l’astronomie médiévale, d’un vice de fond: elles donnent les positions réelles, non les positions jugées telles au moyen âge. Elles seront donc utiles, nécessaires même, pour une comparaison avec d'éventuelles positions «observées», mais, dans la très grande majorité des cas, ces positions calculées rétrospectivement sont trop parfaites: elles sont anachroniques." (ibid.). Hoje, mais de meio século depois e com a pletora de software entretanto disponível, estas considerações são mais pertinentes do que nunca para o estudante da informação astronómica e astrológica que nos chega do passado. Conhecer as ferramentas e os modi operandi do contexto histórico em causa é crucial.

Leitura da informação quantitativa

Zacuto, nas suas tábuas em Castelhano referiu as condições (particularmente os intervalos em longitude) nas quais os eclipses solares se podiam verificar: "Para que sea eclipsi del sol son menester estas condiciones. La primera que el argumento del ancho [i.e. da latitude lunar] al tiempo dela conjuncion verdadera caya dentro delos terminos del eclipse del sol: 5s 1g usque 6s 6g 4min, 11s 23g 56 usque Os 18g. La segunda condicion que la conjuncion sea de dia e non de noche..." (Madrid, Biblioteca Nacional, MS 3385, f. 152r)

As longitudes dos dois intervalos (terminos) citados são as seguintes: de 5 (s)ignos (i.e. 5x30º) e 11º até [usque] 6 (s)ignos e 6º e 4'; de 11 (s)ignos e 23º e 56' até 0 (s)ignos e 18º. Isto é, entre 161º e 186;4º; e entre 353;56º e 18º.

Repare-se que os especialistas actuais utilizam sempre a notação acima utilizada, e.g., 186;4º (=186º e 4'), 353;56º (=353º e 56'). 3;23h (=3 horas e 23 minutos), 365;15,23,29,20... dias (365 dias, 15 horas, 23 minutos, 29 segundos, 10 terços...; era a duração do ano sideral nas Tabelas Toledanas), 0;0,54,30º (0 graus, 0 minutos, 54 segundos de arco e 30 terços; era a precessão anual segundo Albategnius [al-Battani], redundando em ~1º em 66 anos), etc.

Se se tornar necessário converter decimais em sexagesimais (ou vice-versa), o processo é simples. Como exemplos:
4,3 h = 4 horas + 0.3x60 = 4h 18 min. (sexagesimal)
4h 18 min. = 4 horas + 18/60 = 4 horas + 0.3 = 4,3 horas (decimal)

O método matemático de Ptolomeu para resolver problemas com triângulos esféricos havia sido gizado por Menelaus de Alexandria, sendo moroso pois recorria somente às cordas.

Por volta do século IX, os equivalentes medievais das seis modernas funções trigonométricas já eram reconhecidos. O conceito de seno de um ângulo foi introduzido no Islão a partir da Índia, tal como a tangente e a co-tangente, funções importantes nos cálculos envolvendo comprimentos de sombras. Os astrónomos das regiões islamizadas identificaram relações trigonométricas que simplificaram imenso o trabalho com triângulos da esfera celeste.

Escolhendo adequadamente o diâmetro dos deferentes e dos epiciclos, era possível replicar geometricamente (com sofrível aproximação) os fenómenos observados no movimento de um planeta, incluíndo os movimentos retrógrados. No esquema ptolomaico "definitivo", observa-se que se respeitam os movimentos circulares uniformes (ângulos iguais em tempos iguais) quando e somente se observados a partir do ponto equante (aequans). Todavia, como se pode constatar na ilustração, a Terra não está efectivamente no centro. Estes expedientes matemáticos explicavam, como referido, os fenómenos e as irregularidades dos movimentos mas estarão na base de ulteriores críticas ao modelo. nomeadamente por parte dos aristotélicos medievais que "exigiam" que o sistema fosse compatível com os princípios concretos, físicos e naturais, da filosofia de Aristóteles. (Roy, Jean-René, Op. cit., fig. 3-7)

Os expedientes traduzidos no texto de Ptolomeu mitigaram o problema dos movimentos anómalos observados mas serão historicamente, em todo o caso, considerados por alguns como comprometedores dos princípios associados ao movimento circular uniforme, arquetípico (e.g., por Nasīr al-Dīn al-Tūsī e outros astrónomos da tradição Hay'a, i.e. "cosmologia", nomeadamente em Maragha, séculos XIII e XIV). De facto, estes métodos fazem com que o sistema não seja, strictu sensu, "geocêntrico". É em conceito mas não "mecanicamente". Maimónides também havia comentado (no seu "Guia dos Perplexos", finais séc. XII), utilizando argumentos aristotélicos, como seria comum: "I have heard that Abi Bakr [Ibn Bajja, o "Avempace" dos latinos] discovered a system in which no epicycles occur, but eccentric spheres are not excluded by him. I have not heard it from his pupils; and even if it be correct that he discovered such a system, he has not gained much by it, for eccentricity is likewise contrary to the principles laid down by Aristotle... I have explained to you that these difficulties do not concern the astronomer, for he does not profess to tell us the existing properties of the spheres, but to suggest, whether correctly or not, a theory in which the motion of the stars and planets is uniform and circular, and in agreement with observation. (The Guide for the Perplexed, II, 24, trans. M. Friedlander (New York: Dover, 1956), p. 196.). Repudia os expedientes que considera não compagináveis com os princípios aristotélicos e afirma que os modelos astronómicos deverão ser formulados geometricamente, todavia sem relação com a realidade física e as propriedades das esferas, que não eram, para o grande sábio judeu, o múnus do trabalho dos astrónomos.

Segundo Humberto A. de Barros-Pereira, a caracterização de Ptolomeu como "instrumentalista", em oposição ao realismo de Aristóteles, é amplamente empregada devido a P. Duhem, um dos grandes pioneiros da Historia da Ciência que, em Sózien ta phainómena, Essai sur la notion de theorie physique de Platon à Galilée (1908) viu no slogan "salvar os fenómenos", ou "salvar as aparências" a motivação da busca por uma explicação cinemática dos fenómenos celestes. Todavia, como conclui: "Em relação às cosmologias de Aristóteles e de Ptolomeu, podemos distinguir duas maneiras de fazer astronomia no mundo grego-helénico conforme o programa de investigação: a astronomia física, ou cosmologia, de origem aristotélica, que descreve e explica o mundo tal como ele é, na qual o "Hipóteses dos Planetas" [de Ptolomeu] está inserido; e a astronomia matemática, que descreve os movimentos celestes de forma computacional, de origem platônica, na qual o Almagesto [do mesmo Ptolomeu] está situado. Estas duas astronomias, cada qual com suas normas e métodos, são disciplinas distintas e não concorrentes." (Esferas de Aristóteles, círculos de Ptolomeu e instrumentalismo de Duhem, in: História da Física e Ciências Afins, Rev. Bras. Ensino Fís. 33 (2), Jun, 2011).

No Ocidente latino assiste-se à reconciliação dos dois sistemas (aristotélico e ptolomaico). A Filosofia Natural medieval adoptou um compromisso (que de facto havia já sido sugerido por Ptolomeu), distinguindo entre orbis totalis e orbis partialis. Na perspectiva mais abrangente, totalis, o "orbe" ou "céu" do planeta (que pode ser visualizado como o espaço entre duas esferas contendo o aparato de círculos excêntricos necessários à explicação dos seus movimentos), tinha a Terra como centro, centrum mundi (Grant, Op. cit., 445; vide Pierre d’Ailly, XIV Quaestiones..., Quaestio XIII (Veneza, 1531), fol. 163v.).

Quanto às dimensões do Universo, Ptolomeu acreditava que qualquer altura acima da Terra podia ser e era eventualmente ocupada por um, e apenas um planeta. Estimou a distância Terra-Lua equivalendo a 64 raios terrestres. O modelo geométrico para Mercúrio especificava a razão entre a sua altura mínima e máxima e multiplicava-a por 64, e assim sucessivamente. A distância Terra-Lua calibrava as dimensões do espaço das órbitas dos planetas e a distância ao firmamento (no limite máximo de Saturno), v. Hoskin, Michael, The History of Astronomy, Op. cit., 2003. O método clássico de determinação das distâncias de Aristarco, que segundo Ptolomeu foi seguido por Hiparco, baseava-se na observação da amplitude da sombra (da Terra) projectada na Lua durante os eclipses lunares, medindo o tempo decorrido e verificando as paralaxes do Sol e da Lua. O sistema de epiciclos não dava qualquer contributo para a determinação das distâncias dos planetas, somente fornecendo (para cada planeta) o rácio entre os raios do deferente e do epiciclo, em função do comprimento do arco de retrogradação observado. Ptolomeu (nas suas Hypotheseis ton planomenon), expende as distâncias calculadas em raios terrestres, e.g., as estrelas "fixas" estavariam a 19,865 raios terrestres). Com este valor, e não se observando paralaxe, nem se questionava a imobilidade do nosso planeta. A distância maior de um planeta era equivalente à menor do seguinte. As distâncias estão obviamente erradas. Quanto à ordem dos planetas (tirando o caso evidente da Lua), seria algo "incerta" pois as paralaxes eram demasiado pequenas para serem medidas com a tecnologia da época.

Realismo vs. Instrumentalismo na Astronomia Grega

Como James Evans refere (Op. cit., 1998, p.217), na sequência do estudo dos modelos inventados pela astronomia grega a partir de Eudoxus, consolidou-se na História da Ciência uma interpretação segunda a qual os gregos teriam voltado costas à investigação física e estrutural do Universo, em detrimento da agilização de expedientes que acautelassem os fenómenos observados, que aparentemente reproduzissem os movimentos irregulares dos corpos celestes. Esta interpretação "instrumentalista" foi populatizada por P. Duhem (Sauver les apparences, 1908), J. L. E. Dreyer e A. Koestler, que escreveu:

"The astronomer "saved" the phenomena if he succeeded in inventing a hypothesis which resolved the irregular motions of the planets along irregularly shaped orbits into regular motions along circular orbits — regardless whether the hypothesis was true or not, i.e., whether it was physically possible or not. Astronomy, after Aristotle, becomes an abstract sky-geometry, divorced from physical reality... It serves a practical purpose as a method for computing tables of the motions of the sun, moon, and planets ; but as to the real nature of the universe, it has nothing to say." (Koestler, A., The Sleepwalkers, The Macmillan Company, New York, 1959, pp.73-4)

Todavia, a realidade é provavelmente mais complexa. A astronomia grega primitiva estava muito mais preocupada com a uma ampla explicação natural do que com os detalhes da explicação rigorosa dos fenómenos que, de facto, não conseguia proporcionar. A abordagem preditiva rigorosa é relativamente tardia, desenvolvendo-se somente na época de Hiparco. Mesmo então, as discussões acerca da preferência pelo uso de deferentes ou de epiciclos não estavam evidentemente isentas de considerações acerca da sua realidade concreta. Os progressos de Hiparco, os cálculos de distâncias e diâmetros, até o da própria circunferência da Terra, o Ptolomeu das "Hipóteses Planetárias"... todos demonstram que os modelos seriam potencialmente tomados como realidades concretas. Havia instrumentalismo mas almejava-se o realismo.

A Idade Média (percurso dos saberes após o declínio das instituições de suporte do saber clássico no Ocidente Latino)

No Quarto Dia da Criação, os corpos celestes começaram a revolver em torno da Terra. (Hartmann Schedel, Liber Chronicarum, Nuremberg, Antonius Koberger, 1493 [Huntington Library, RB 95858)

A Idade Média legou-nos, entre outros contributos, duas instituições fundamentais: a Universidade (com origem europeia, quando a erudição escolástica se consolida) e, no contexto Islâmico, o Observatório (todavia, sondar os segredos dos céus era visto com desconfiança pelas autoridades religiosas e os observatórios foram efémeros). Mas esta época não foi decerto uma "Idade das Trevas" (conceito de Petrarca e, mais especificamente, baseada em saeculum obscurus, expressão utilizada pelo Cardeal Caesar Baronius no início do séc. XVII para referir a ausência de fontes documentais nos sécs. X e XI, sem intenção pejorativa).

Historicamente, os textos mais influentes (início da Idade Média) são provavelmente o longo comentário neoplatónico de Calcidius ao Timaios ("Timeu", diálogo cosmológico de Platão) e De nuptiis Philologiae et Mercurii de Martianus Capella, fonte inestimável de informação sobre o elenco disciplinar no contexto das Artes Liberais (onde, acolitando a philologia, cada uma das artes se apresenta, personificada, explicando a sua incumbência), influenciando a estrutura do ulterior ensino académico europeu: o trivium e o quadrivium. A Astrologia, como um todo, fará parte do Quadrivium, o segundo patamar das chamadas Artes Liberais. Aristóteles e Ptolomeu somente estarão acessíveis no século XII através de uma vaga de traduções.

A Filosofia apresenta a Boécio as Sete Artes Liberais; De consolatione philosophiae, de Boécio (Boethius, c.480–524); Francês, c.1460-70 (The J. Paul Getty Museum, Ms. 42 [81.MS.11], f.2v)

O ensino na Antiguidade tardia e na Idade Média consistia, em teoria, nas sete Artes Liberais. Antes, já Varrão (Varro), século I a.C., havia identificado um cânone de nove artes liberais consideradas essenciais para a educação romana. O nome latino Artes Liberales, refere-se às artes ou competências adequadas ao "homem livre", em oposição ao escravo.

A palavra "liberal" não está aqui relacionada com "liberalidade" ou "liberalismo": significa aqueles saberes adequados ao homem livre. Ora, os homens livres não precisavam trabalhar, pelo menos manualmente. O que eles utilizavam acima de tudo eram as palavras: nos tribunais, na política, em polémicas e argumentações. Consequentemente, a sua educação devia ser praticamente "inútil" excepto para fazerem discursos ou escreverem livros [todavia gozando de um prestígio incomparavelmente superior ao das artes 'mecânicas']. Portanto a Educação Grega, e depois a Romana, era fundamentalmente retórica. Houve tentativas para integrar disciplinas práticas como a Arquitectura ou a Medicina (ambas respeitáveis), sem sucesso duradouro. É desta tradição Greco-Romana que emana o preconceito que favorece as artes intelectuais e predominantemente verbais em detrimento das manuais. Esta era uma tradição que servia adequadamente a burocracia da Igreja.

Foram, por volta do século VI, divididas em dois grupos: o mais elementar Trivium (Gramática, Retórica e Lógica); e o Quadrivium (Aritmética, Geometria, Música e Astronomia). A divisão traduzia a separação dos graus de dificuldade e as etapas da instrução: um conhecimento da Gramática, Retórica e Dialética era necessário para o estudo das restantes quatro. Portanto, o Trivium constituia o estágio elementar, daí o termo "trivial". A Gramática era aquilo que o nome indica, sendo sinónomo de 'Gramática Latina'. Na maior parte dos casos, pelo menos até à adopção do tratado de Prisciano (Institutiones Grammaticae) se tornar comum, no séc. XI, os manuais eram trabalhos muito breves de Donatus, autor do séc. IV. Quando os rudimentos eram assimilados, liam-se os clássicos: primeiro e em particular a Eneidade Virgílio e depois extractos de autores como Terêncio, Horácio, Ovídio ou Estácio, todos incluidos em antologias escolares. A Retórica eram as figuras de estilo, modalidades oratórias, métricas e artifícios literários. A combinação da Gramática e da Retórica permitia um treino linguístico suficiente, e muitos estudantes, mesmo na Antiguidade, não iam mais além. Por 'Dialética' entendia-se a Lógica Aristotélica, que não era tão acessível e parecia menos relevante. Todavia, foi a partir da Dialética [i.e. da Lógica, cujo foco era a contraposição e contradição de ideias que levavam a outras ideias] que se propiciou o aparecimento da filosofia Escolástica, pois levantava muitas questões pertinentes enquanto disponibilizava parcas sugestões de respostas.

O Quadrivium era pouco estudado, tanto na Antiguidade como no início da Idade Média, mas era, em tese, considerado necessário para o cabal entendimento das Escrituras. A Aritmética não era o que hoje assim designamos: a isso chamava-se "Algorismo", somente introduzido no séc. XII. Os cálculos eram efectuados com o recurso a ábacos e a Aritmética não se preocupava com os cálculos mas sim com os Números, incluindo, entre outras coisas, as suas 'formas' (por isso continuamos a utilizar termos como "quadrado", e.g., 8; ou "cubo", e.g., 9). A Geometria incluia tanto a geometria elementar como a 'geografia', a descrição do Mundo e das suas regiões; ambas podiam ser chamadas "medição da terra", o significado literal da palavra "geometria". A Música, como a Aritmética, estava muito pouco relacionada com o exercício instrumental concreto, mas muito com as teorias da Harmonia [das Proporções], seus modos e efeitos na alma humana. Finalmente a Astronomia era a 'Astrologia' (conjunto da Astronomia e Astrologia), incluida desde o início nos estudos avançados. Ambos os nomes latinos são utilizados de modo diverso ou intercambiável, mas até ao séc. XII o seu conteúdo é quase inteiramente do jaez a que hoje chamaríamos "astronómico".

A Música - Como Joscelyn Godwin explica, os antigos conheciam a Musica mundana, a música do cosmos; Musica humana, a da entidade humana; e a Musica instrumentalis, cantada e interpretada. A Musica Humana analisa o Homem como microcosmos, reflectindo a ordem cósmica. As partes do seu corpo são governadas pelos signos, os seus sete órgãos internos pelos sete planetas e os seus quatro humores correspondem aos elementos. Ele também aloja um elemento subtil ou espírito vital, e uma alma que, como os platonistas asseveram, é composta 'harmoniosamente'. A Musica Humana procura colocar este conceito em prática. Foram os Pitagóricos quem primeiro formulou a ideia de que diferentes modos musicais tinham efeitos específicos no corpo e na alma ("Music? What does that have to do with esotericism?", in: Hanegraaff, W, Forshaw, P. & Pasi, M., (eds.), Hermes Explains: Thirty Questions about Western Esotericism, University of Amterdam Press, 2019, p.115). Hildegarda de Bingen (a "Sibila do Reno"), abadessa do mosteiro beneditino de Rupertsberg, mística e polímata do século XII, descreveu nas suas "Harmonias Divinas" a música (teológica) como um meio para recapturar a pureza original do Paraíso, pois antes da "Queda", a voz de Adão juntava-se à dos Anjos em louvor a Deus. Depois, tornou-se necessário inventar a música e os seus instrumentos. Também foi, de acordo, prolífica compositora (Symphonia armonie celestium revelationum).

Todavia, o esquema das sete artes liberais não era um currículo estudado como um todo, nem era rígido ou incapaz de evolução. Uma perspectiva da expansão do antigo esquema pode ser vislumbrada nos séculos XII e XIII, comparando os esboços de três curricula. O primeiro é de Cassiodorus (que relaciona Liberales com liber, "livro"), que no início do séc. VI sucedeu a Boécio (Boetius, autor da célebre De consolatione philosophiae) como secretário de Teodorico, o rei Ostrogodo da Itália, e que, aposentado, redigiu dois trabalhos de índole pedagógica para a instrução monástica, conhecidos como Institutiones. Lista os manuais adoptados na vertente secular, com destaque para Boetius e Martianus Capella [no De nuptiis Mercurii et Philologiae deste último são elencadas as sete disciplinas liberais, divididas num grupo dedicado à palavra e noutro cometido à ciência dos números e medições], São os únicos autores atribuídos ao estudo da 'Astrologia'. Em 1142, Thierry de Chartres redigiu um silabário enciclopédico, para utilização na sua escola. Continua a ser oficialmente enquadrado nas sete artes mas agora prevalece a "nova lógica" (fruto das traduções recentes dos principais trabalhos de Aristóteles, recém-chegados às escolas). Também elenca quatro "autoridades" para a Geometria (incluindo Gerbert d’Aurillac, finais do séc. X, Bispo de Rheims [actual Reims] e futuro Papa), o livro de Garlandus "Compotista" sobre a utilização do ábaco (De abaco) e, na Astronomia, Hyginus, Ptolomeu (Ptolemaeus) e al-Khwarizmi (de cujo nome a nossa palavra "algarismo" é uma corrupção). Outro exemplo curricular de uma Faculdade de Artes medieval é o proveniente de um manuscrito catalão de Ripoll (c. 1230-1240). Aqui, as antigas "artes" (na componente mais básica) desapareceram. A philosophia é dividida em três partes: 'Natural', que inclui a Metafísica, a Física e a Matemática (sendo que a última equivale ao antigo Quadrivium, onde surgem Euclides na Geometria e Ptolomeu - i.e. o Almagesto - na Astronomia). Na segunda divisão, a Filosofia Moral, inclui-se a Ética de Aristóteles. A Filosofia Racional (que equivaleria ao Trivium) consistia quase inteiramente na Dialética. Neste tipo de currículo, as ciências desenvolveram-se, evidentemente, a partir da Filosofia Natural.

Uma gravura de 1504 da Margarita Philosophica, texto tardo-medieval de Georg Reisch, representa a organização dos estudos de Artes, muito depois da assimilação dos textos traduzidos. A partir da base, a Gramática e a Retórica são representadas por Donatus, Prisciano e "Tullius" (Cícero), Boécio representa a Aritmética, Aristóteles a Lógica, Pitágoras a Música, Euclides a Geometria e Ptolomeu a Astronomia, culminando com a Teologia (Lombardo, i.e. Petrus Lombardus, autor das "Sentenças", em quatro livros: Libri Quattuor Sententiarum)

Em resumo, as fontes principais foram Martianus Capella (De nuptiis Philologiae et Mercurii) e Macrobius (no seu comentário ao Somnium Scipionis de Cícero). Ambos do início do século V, escreveram em Latim, num estilo enciclopédico. A recolecção de materiais de Martianus, articulada com Macrobius é geralmente considerada importante por ter tornado canónicas as sete Artes Liberais. No Livro VIII das "núpcias", a personificação da Astronomia inicia a sua prelecção explicando como o Universo é uma esfera composta por quatro elementos, e como os "físicos" declaram que existe um quinto aglomerado de matéria, no qual os corpos celestes se movem. Explica como tudo isto foi aprendido ao longo de quarenta mil anos (!) em contacto com os conhecimentos secretos do Egipto antigo. A sua dívida de gratidão vai para o "Cilénio" [i.e. Hermes/Mercúrio, que o mito grego fez nascer no monte Cilene], que a adoptou e educou. Refere também a disseminação desse conhecimento (os gregos Eratóstenes, Ptolomeu e Hiparco são aqui mencionados). O terceiro autor a considerar é outro enciclopedista: Isidoro de Sevilha. No currículo (mais básico) das Artes, para além do conhecimento do computus, as prelecções obrigatórias versavam o De sphera de Sacrobosco, do qual havia diversos comentários. Segundo J. D. North, existia, no séc. XIV, uma ambição académica em articular uma "representação do Mundo" completa e ordenada, mas imbuída de sentido teológico. A alegoria da passagem da alma humana da terra ao paraíso, de Dante, é um excelente exemplo que revela algumas das dificuldades de reconciliação de um Universo geocêntrico com um tipo de discurso religioso teocêntrico. Já na "Consolação da Filosofia" (De consolatione philosophiae) de Boécio, esta visão procurara gerir a inconsistência de um mundo evidentemente desorganizado através de um engenhoso expediente: a mutabilidade é entendida como parte da mais abrangente estabilidade imposta por Deus (Chaucer's Universe, Oxford, Clarendon Press, 1988, p.10).

Antes, na Alta Idade Média assistira-se a uma necessidade premente de coligir informação calendárica com propósitos litúrgicos, nomeadamente a determinação da data da Páscoa. O célebre computus é finalmente "normalizado" por Beda, o "Venerável". Desde a época Carolíngia (c. 800 AD) que as escolas monásticas são acompanhadas por escolas de burgo, nas catedrais. Prestava-se particular importância aos fenómenos elementares de astronomia esférica. O mito das "trevas" medievais europeias já foi dissipado há muito tempo. Bruce Eastwood e Gerd Graßhoff referem-no claramente, particularmente tendo em consideração a riqueza do legado Carolíngio:

"From the sixth to the twelfth centuries in western Europe, it has long been assumed that there was no scientific development of any significance. (...) Studies in recent years, especially from the 1970s forward, have begun to change our view of Carolingian sciences. In his lengthy directions to the clergy in 789, the Admonitio generalis (General Directives), Charlemagne required the study not only of grammar, writing, and chant, but also of computus. Is possible to categorize computus as the arithmetical computation of the date of Easter and all the other feast days of the Christian calendar that depend on it. However, this definition presumes much and omits more. It presumes the basic luni-solar astronomy behind the determination of the equinoxes, basic to any Easter dating, and it omits a body of knowledge about the twelve signs of the zodiac that came to be part of computistical competency in the Carolingian era, if not earlier." (Eastwood & Graßhoff, Planetary Diagrams for Roman Astronomy in Medieval Europe, ca. 800-1500, American Philosophical Society, Transactions of the American Philosophical Society, Philadelphia, vol. 94, Part 3, 2004). Os autores acrescentam que desde a época do Imperador (Carlos Magno), se encontram evidências inequívocas de um estudo sério e investigação de matérias astronómicas tanto na corte como em ambientes clericais. Como já abordamos em parte, as fontes romanas essenciais na época foram Plinius "o Velho" (Nat. Hist.), Marcianus Capella (De Nuptiis Philologiae et Mercurii), o comentário de Macrobius ao Somnium Scipionis de Cicero (onde Macrobius descreve uma cosmovisão que erradamente atribui a Platão) e o comentário de Calcidius ao Timaios.

Nesta época ganha visibilidade um "sistema" geo-heliocêntrico patente em Martianus Capella (séc. V) e divulgado numa tradução do neoplatonista Johannes Scotus Eriugena (séc. IX) onde Mercúrio e Vénus orbitam o Sol e este último (bem como os planetas mais distantes) orbitam a Terra estacionária (voltaremos a encontrar este sistema adiante): "Hunc, ut comites, consequuntur, Veneris alter, alter Mercurii cursus" (Cícero, Somnium Scip., IV); ou seja, seriam companheiros ou "satélites" do sol (comites solis). Era atribuído aos "Egípcios". Mais tarde Copernicus chamou a atenção para esta peculiaridade, que ele e outros consideravam interessante no sistema de Martianus (acerca desta e outras interpretações "heliocentristas", todavia consideradas textualmente ténues, vide O. Neugebauer (1975), HAMA, vol. III, section IV C 2, 2).

Sistema de Martianus Capella (Ms. Laur. San Marco 190, f. 102r)

Diagrama compósito com aspectos da teoria planetária de Martianus Capella, datado do séc. IX. Acima da Terra (desenhada de modo peculiar, em forma de "gota") e da Lua (representada pelo crescente), representa-se o Sol (Phoebus) com os circuli dos planetas Stilbon (Mercúrio) e Phosphorus (Vénus). O desenho quase sugere um heliocentrimo aparente. Contudo, o Sol é desenhado no "centro" mas é a Terra excêntrica que ocupa o centro da órbita anual do Sol e dos planetas exteriores. (Biblioteca Medicea Laurenziana (Ms. Laur. San Marco 190, f. 102r; uma cópia do séc. XV encontra-se no Ms. Urb. lat. 329 (f.139v), da Biblioteca Apostolica Vaticana, ver). Em baixo, um detalhe de diagrama num tratado anónimo (Ms GKS 277 2º, f.49r, Det Kongelige Bibliotek [Biblioteca Real], Copenhaga). Saliente-se que as rotae (obviamente circulares) constituiram um modelo privilegiado de exposição da informação complexa ao longo de toda a Idade Média.

Uma força ("vis") associada aos raios do Sol seria, para Plinius e Martianus Capella, responsável pelos movimentos planetários, suas estações (paragens) e retrogradações. Martianus considera que os dois planetas mais próximos do Sol, estando mais "subjugados", orbitavam segundo círculos com dimensões impostas pelos mencionados raios. E expende esse interessante conceito de órbitas circum-solares: "It was solar radial force, not epicycles, that explained the bounded elongations for Martianus. He seems to have imagined that the solar force transformed the Plinian oscillating motions of the inner planets into closed circles around the Sun, binding them within the visual angles of 22º (or 23º) and 46º from the Sun, assigned respectively to Mercury and Venus by both Pliny and Martianus. The outer planets could not be bound in this way because of their greater distances from the Sun, thus limiting the effects of its radial force on them." (Eastwood, Ordering the Heavens, Roman Astronomy and Cosmology in the Carolingian Renaissance, Leiden; Brill, 2007, p.292). O tópico da sequência dos planetas também era importante: "The topic of the order of the planets from the earth to the stellar sphere could be called one of the astronomical questions of the day in the first half of the ninth century, because Macrobius simply presented two fixed orders and chose what he took to be Plato’s order in preference to that of the Chaldeans. Pliny, while agreeing with the Chaldeans and being supported by early medieval authors like Isidore and Bede, gave no argument to prove the superiority of his order. Only with the spread of Martianus Capella’s doctrine of circumsolar Mercury and Venus was there the beginning of a reconciliation between the two opposed views on the sub-solar versus the supra-solar locations of Mercury and Venus." (ibid, p.317). E será em Calcidius que a época Carolíngia encontrará a primeira explicação do funcionamento de um epiciclo simples, algo que Martianus Capella não abordou.

Depois existia o "firmamento" (non errantium stellarum sphaera) com as estrelas fixas. Em linha com o relato bíblico, acreditava-se comummente nas "águas superiores", um cristalino de águas congeladas acima do firmamento (que impediam que o mundo se incinerasse devido ao fogo celestial, uma ideia disseminada pela literatura patrística, vigorosamente defendida, por exemplo, por Cirilo de Jerusalém [Cyrillus Hierosolymitanus, séc. IV]). Acima destes céus, mais distante, o Empíreo dos bem-aventurados. Sendo invisíveis, estas duas últimas esferas "teológicas" não eram do âmbito astronómico.

Assistimos, portanto, a uma "dolorosa" articulação com as Escrituras, amiudadamente promovendo um desconforto com o conhecimento da Natureza. Severianus, bispo de Gabala (Síria), nas "Orationes sex in mundi creationem" (Migne, Patr. Gr., LVI, 429-500) interpretava o Universo não como uma esfera mas como uma tenda ou um tabernáculo. Os argumentos que remetem para esse difundido paradigma encontram-se em autores como Theodorus de Mopsuestia (na Cilícia), séc. V, que conhecemos através das críticas de Philoponus (um cristão neoplatónico alexandrino), Diodorus de Tarsus, etc. S. Basílio Magno, apesar da sua erudição, afirmou que Moisés nada nos disse acerca da figura da Terra ("que muitos disputam se é uma esfera, um cilindro ou um disco, ou se é vazia por dentro"), porque se trata de coisas que não precisamos de saber (Homiliae noven in Hexaemeron, ix, 1,1c). No limite, autores como Lactâncio (Lactantius, c. 250 - c. 325, conselheiro de Constantino I), inimigo da cultura pagã e do conceito da esfericidade da Terra, que ridicularizou (Institutiones Divinae, 3.24: De antipodibus, de coelo ac sideribus ["Sobre os antipodas, o céu e as estrelas"]), ou o monge Cosmas Indicopleustes, lit. "viajante das Índias", séc. VI, (que na sua "Topografia Cristã" representou o mundo segundo um paralelogramo que tinha, justamente, o seu arquétipo no Tabernáculo vetero-testamentário), assumiam uma agressiva interpretação teológica literalista. O próprio Isidorus Hispalensis (i.e. "de Sevilha", séc. VII), na época celebrado pelo seu saber, refere que a luz das estrelas é recebida do Sol e, de resto, acumula dislates quanto aos períodos de revolução da Lua e dos planetas.

Numa perspectiva geográfica mais evoluída, e tal como Martianus Capella, Macrobius expendia a teoria de Crates de Malos (século II a.C.), segundo a qual a Terra estava dividida pela água em quatro massas ("quartos"), todos habitados e um dos quais era a nossa ecúmena (v. pág. globo terrestre).

S. Ambrósio de Milão (séc. IV) reconhece a esfericidade da Terra, mantendo contudo uma firme crença nas "águas superiores". S. Agostinho de Hipona mantém a mesma perspectiva mais "aberta", pois reconhece que a Terra pode ser esférica. Mas preocupa-o o problema dos antípodas, argumentando que essa parte do mundo pode não estar emersa e, mesmo estanto, pode não ser habitada (se o fosse, questiona, como é que esses descendentes de Adão aí poderiam ter chegado?). Mais tarde, Beda expendirá os rudimentos da estrutura do Universo, particulamente no De natura rerum, seguindo Plínio. Em todo o caso, ainda refere as famigeradas "águas" supra-celestes. [A proximidade de Saturno a essas águas era uma das explicações comuns na época para a frigidez do pálido e distante planeta.] No De tempore ratione, o Venerável demonstra o conhecimento dos principais fenómenos celestes, calendáricos e cronológicos. No séc. IX, Rábano Mauro (Hrabanus Maurus), o culto abade de Fulda e Mogúncia, no De universo libri xxii, sive etymologiarum opus (influenciado pelas Etymologiae de S. Isidoro), vai procurar "conciliar" a rotundidade do orbe, que reconhece (xii, 2), com o texto das Escrituras, que mencionam "os quatro cantos" do mundo. Uma tarefa difícil. Também (ainda) menciona as duas "portas do céu" (no oriente e no ocidente) que o Sol atravessaria diariamente (ibid., ix, 5: De januis coeli: "Januae coeli duae sunt: Oriens et Occasus. Nam una porta sol procedit, alia se recipit"). Em alguns destes casos estamos tão somente perante interpretações de passagens bíblicas, formulação de sentido teologicamente relevante num contexto particular que não é comparável com a abordagem literalista de Lactâncio. Mais tarde, já no séc. XII, o género enciclopédico, tanto ao gosto medieval, tem uma referência importante em Honório de Autun (Honorius Augustodunensis), cuja Imago mundi, uma enciclopédia de cosmologia e geografia popular combinada com um crónica da história universal, intersecta (na exposição cosmológica) o tradicional resumo de Plínio (incluíndo os planetas, suas distâncias e respectivos intervalos musicais) com a descrição dos loci do imaginário sagrado: o Paraíso fica no Céu espiritual (i.e. o que foi originalmente criado, o dos anjos que estão alojados segundo nove "ordens"), acima do redondo do firmamento das estrelas e, claro, também acima das "águas", que aqui são nuvens; o Inferno, inversamente, situa-se no centro da Terra. Uma organização hierarquizada que, mais elaborada, reconheceremos na magnífica visão poética de Dante. Também os mapas coevos eram veículo de uma geografia sagrada: Jerusalém era o Omphalos do mundo, no centro da ecúmena; desenhava-se o Paraíso, as terras de "Gog e Magog", etc.

Voltando à abordagem 'científica' estrita, as fontes anteriores às traduções a partir do Árabe foram, principalmente, Plinius, Calcidius, Macrobius, Martianus Capella e Isidorus (Isidoro de Sevilha). Mas nenhum destes autores ensinou como localizar os planetas (i.e. conhecer as suas longitudes) nos signos zodiacais. O material relevante para esse cálculo, habitualmente disponível em tabelas, apenas se tornou acessível com a tradução de al-Khwarizmi e com as chamadas Tabelas Toledanas. [O estudo dos exempla históricos recorre, na literatura actual, à comparação com as efemérides de referência de B. Tuckerman: Planetary, Lunar and Solar Positions A.D. 2 to A.D. 1649 at Five-Days and Ten-Days Intervals, Philadelphia, 1964]. Antes das traduções das tabelas e dos seus cânones, somente os ciclos do Sol da Lua eram estudados devido à sua importância no Computus (cuja função era servir o Calendário Eclesiástico). O cômputo possuía os seus textos de suporte, por exemplo o de Hrabanus Maurus (baseado na obra de Beda e redigido no ano de 820). Alguns outros fenómenos astronómicos (e.g., eclipses, conjunções) são referidos por autores desses séculos como simplesmente observados ("visa est"). Mas existiam métodos rudimentares para conhecer o signo em que estavam os planetas, em particular os mais lentos e menos "complicados". Segundo David Juste: "Whatever the case, the examples of Rabanus Maurus and the Annales regni Francorum show that it was possible both to obtain precise positions of the luminaries by means of elementary rules of computus and to observe the position of the planets (at least Saturn, Jupiter and Mars) in the correct signs." (Juste, D., Neither Observation nor Astronomical Tables: An Alternative Way of Computing the Planetary Longitudes in the Early Western Middle Ages, in: Burnett, C., Hojendijk, J. & Yano, M., (eds.), Studies in the History of Sciences in Honour of David Pingree, Brill, 2004, p.189). Outro método elementar utilizava (ibid., p.189 et seq.): (1) as posições dos planetas no thema mundi ou genitura mundi de Macrobius e Firmicus Maternus (2) os períodos zodiacais dos planetas e (3) o tempo decorrido desde a Criação (vetero-testamentária) do Mundo: 5199 anos de acordo com a versão Septuaginta Grega ou 3952 anos de acordo com a tradição hebraica. Uma variante desta metodologia surge no Liber Alchandrei (e em outras duas fontes estudadas por Juste). Segundo o historiador, a colectânea de textos conhecida como "Alchandreana" constitui a mais antiga manifestação, no Ocidente Latino, de um conjunto de teorias (e.g., movimentos planetários, mansões lunares, casas mundanas, nodos lunares) a partir de fontes árabes e hebraicas (v. Les 'Alchandreana' primitifs: Étude sur les plus anciens traités astrologiques latins d'origine arabe (X.e siècle), 2007). O Liber Alchandrei pertence a essa colecção primitiva que deu entrada no mundo Latino a partir da Espanha, coligido na Catalunha na segunda metade do séc. X (Juste, D., Neither Observation nor Astronomical Tables..., Op. cit., p.200). Antecedentes dos curiosos (e imprecisos) métodos elementares já se encontram em Vettius Valens (Anthologiae, 1.18, ed. D. Pingree, Leipzig, 1986, pp. 32-6), [cf. Cristian Tolsa, Vettius Valens’ Longitudes (1.18), Balbillus, and the Illusion of Astrology’s Self-sufficiency, Universität Osnabrück, 2019] e em fontes bizantinas. Nas fontes gregas o referente inicial é a Era de Augustus (=29 de Agosto de 31 a.C.), com excepção para a posição do Sol, calculada para o annus mundi 6414.

Mas cosmologicamente permanecia a questão da misteriosa "força" que moveria as esferas descritas na Antiguidade. Deus era a Causa Primeira e talvez a hierarquia teológica dos angelicais seres intermediários estivesse encarregada das esferas interiores, cada uma com a sua entidade incumbente (e.g., Serafins, Querubins, Tronos), seguindo o pseudo-Dionísio Areopagita (séc. V ou início do VI), que procurou trazer o Neoplatonismo, principalmente o de Proclus e o da Academia, para o contexto cristão. Buridanus, (Jean Buridan, séc. XIV) procurou uma explicação mais mecânica e retomou o conceito do Impetus (força motivadora, precursora do moderno conceito de 'inércia'). Assim, numa envolvente matérica quintessencial, não sujeita ao atrito, o impulso inicial de Deus no momento da Criação seria suficiente para perpetuar o movimento. O seu aluno Nicolas Oresme (1323-1382) defenderá este princípio, bem como a ideia de espaço infinito. A própria tendência aristotélica dos corpos para o "lugar natural" será gradualmente entendida como tendência para se juntar ao semelhante e não tendência para o centro, descartando a noção de "leveza" que se contrapunha ao comportamento dos "graves". E Nicolau de Cusa (Nikolaus von Kues, 1401-1464) descreverá um Universo infinito, mostrando como uma vanguarda de novas perspectivas fervilhava em certos ambientes tardo-medievos e renascentistas.No Docta Ignorantia de Nicolau de Cusa lê-se:

"Life, as it exists here on earth in the form of men, animais and plants, is to be found, let us suppose, in a higher form in the solar and stellar regions. Rather than think that so many stars and parts of the heavens are uninhabited and that this earth of ours alone is peopled - and that with beings perhaps of an inferior type - we will suppose that in every region there are inhabitants, differing in nature by rank and all owing their origin to God, who is the centre and circumference of all stellar regions." (trad. Inglesa de Steven J. Dick, Plurality of Worlds: The Extraterrestrial Life Debate from Democritus to Kant. Cambridge University Press, 1984, p.41; orig. em Latim editado por Hoffman & Klibansky, Lipsiae, 1932, p.107).

Em breve se colocarão outras hipóteses arrojadas, com mundividências admitindo um Universo infinito ou a pluralidade dos mundos (e.g., as de Giordano Bruno e de Thomas Digges). A visão do primeiro é muito ampla e até relativista (muito para além de simplesmente "heliocêntrica", como é amiudadamente referido), advogando a pluralidade dos mundos [a habitabilidade de outros "mundos"], a relatividade do centro (i.e. a ilusão de estar no centro do Universo, comum aos hipotéticos habitantes de qualquer corpo celeste) e a infinitude espacial. Segundo Garin (p.131), no De immenso, Bruno, em nome da imanência da unidade divina da natureza, condena o céu dividido das esferas e vê Copernicus como um libertador, não tanto porque colocou o Sol no lugar da Terra, mas porque destruiu a esfera celeste dos "estultos matemáticos". Mais tarde, na nova astronomia e no pensamento pós-aristotélico, abre-se a oportunidade para novas especulações. Kant, em 1755, concluia que quase todos os planetas "devem ser habitados"; os que agora não são, virão decerto a sê-lo. O espírito da época [das "Luzes"] concebia com naturalidade essa possibilidade.

N'A Criação do Mundo e Expulsão do Paraíso de Giovanni di Paolo, 1445, Deus parece imprimir o ímpeto inicial ao Cosmos (Metropolitan Museum of Art, New York)

Voltando ao nosso fio histórico, como Olaf Pedersen resumiu (European Astronomy in the Middle Ages, in: Walker, C. (ed.), Astronomy Before the Telescope, British Museum Press, 1996), a "explosão" do conhecimento no século XII determinará a emergência de escolas especializadas (sob orientação de diversos mestres e vocacionadas para uma área específica, e.g., Bolonha surge associada às Leis, Montpellier à Medicina, Paris à Teologia, Chartres à Filosofia Natural, etc.). Deste contexto vai surgir a agregação multidisciplinar, gerando o chamado studium generale ou "universidade", numa estrutura comum com diversos tipos de organização corporativa. Exigia-se a frequência pretérita da formação básica da "Faculdade de Artes". Desta formação elementar fazia parte o estudo da astronomia (Astrologia) como parte integrante da Filosofia Natural, bem como da Filosofia Moral e da Metafísica. O currículo generalizava o acesso aos rudimentos da astronomia e cosmologia mas não se encontram estes saberes trabalhados a um nível mais elevado, ao contrário da Lei, da Medicina ou da Teologia. A basicidade reflectiu-se na utilizaçao de exposições simplificadas do Almagesto e no recurso ainda mais comum a manuais acessíveis como o Tratactus de Sphera (elementos de astronomia esférica), o "Compotus" (calendário e as datas litúrgicas) e o Algorismus (explicando como efectuar operações com os novos numerais). As parcas informaçoes de Sacrobosco acerca dos modelos cinemáticos planetários ptolomaicos eram complementadas com o anónimo Theorica planetarum (estando disponíveis diversos textos análogos de diferentes autores). Muitas vezes todos ou boa parte destes textos descritos eram coligidos (com tabelas associadas) num Corpus astronomicum, a melhor ferramenta de trabalho até ao século XVI, tendo avançado para versões impressas. Com a disseminação da cosmologia aristotélica (harmonizada com a teologia Cristã pelo influente Tomás de Aquino, 1225-1274), a motivação fundamental passou a ser o estudo das causas dos fenómenos (em detrimento da concomitante tradição antiga da descoberta de relações matemáticas entre os fenómenos naturais). Cosmologicamente, o texto fundamental é o Meteorologica ou Meteora. O aristotelismo estrito perfila o seu comentador Averróis (ibn Rushd) e sente-se desconfortável com os expedientes anómalos (e.g., epiciclos) que compromentem a pureza do sistema homocêntrico. Outra atitude procura a explicação matemática dos fenómenos em detrimento da explicação estrutural. As Hipóteses Planetárias de Ptolomeu (não incluídas no seu conhecido compêndio) serão utilizadas e adaptadas com sucesso, por exemplo na Theorica de Campanus de Novara.

Entretanto, assiste-se ao retorno da prática astrológica, em maior ou menor grau, através da "ressurreição" de Platão (a relação Macrocosmo-Microcosmo), da tradução de autores Islâmicos (Abu Ma'shar, conhecido como Albumasar, al-Qabisi, o conhecido Alcabitius, etc.) e, claro, do Tetrabiblos de Ptolomeu. A própria noção aristotélica do Primum Mobile e das suas influências "causais" contribuiu para a relevância da doutrina das influências (e.g., na Medicina), mas sempre com desconforto eclesiástico, particularmente devido à questão livre arbítrio versus determinismo.

A síntese do dominicano Tomás de Aquino (1225-1274), inicialmente contestado mas ulteriormente canonizado, permitirá consolidar o papel da Philosophia Naturalis e da Razão na abordagem ao divino. Uma "ousadia", atendendo à pretérita predominância do pensamento de Santo Agostinho, que filosoficamente se respaldava em conceitos do platonismo (no qual os arquétipos ou ideias é que são verdadeiros, "reais" e pertinentes). Aquino abraçou as ideias de Aristóteles - a que se referia como "O Filósofo" - e sintetizou a filosofia aristotélica (onde prevalecem a lógica dedutiva e método analítico indutivo no estudo da natureza e leis naturais, bem como as conhecidas "Categorias" que classificam e analisam os dez tipos de predicados ou géneros do ser (κατηγορία significa justamente "predicado"), i.e. as dez categorias segundo as quais qualquer objecto no mundo poderia ser classificado) com os princípios do Cristianismo. Aceitou o uso da razão na especulação teológica. A almejada harmonia entre Teologia e Filosofia (prevalecendo hierarquicamente a primeira), entre fé e razão, encontra paralelos em outros âmbitos, como entre Igreja e Estado, e, em última análise, entre Deus e o Homem.

Mas levantavam-se dificuldades. Para Aristóteles o Mundo sempre existira e o Universo era eterno. Isto estava em contradição com as Escrituras, com o relato bíblico. Também há desacordo com Santo Agostinho nas concepções sobre a alma humana e, de modo abrangente, no plano epistemológico. Em 1270 o bispo de Paris, Étienne Tempier, publicou um édito condenando treze proposições aristotélicas e averroístas como heréticas e excomungou os que continuavam a defendê-las. Enquadravam-se em quatro rubricas: eternidade do Mundo, negação da Providência Universal, unicidade da alma intelectiva ("monopsiquismo" ou partilha de uma mesma alma eterna) e determinismo. De resto, muitos eclesiásticos "agostinianos" temiam que a introdução do aristotelismo e da sua versão mais extrema, o averroísmo, pudesse de alguma forma contaminar a pureza da fé cristã. [Aquino é influenciado pelo averroísmo mas distancia-se, particularmente da já mencionada ideia da unicidade da alma ou da mente, também da negação da imortalidade da alma como um todo.] Em Março de 1277, o mesmo bispo publicou outro édito, mais amplo. Um dos objectivos desta vez era clarificar que o poder absoluto de Deus transcendia quaisquer princípios da Lógica de Aristóteles ou de Averróis. Continha uma lista de 219 proposições que, segundo o bispo, violavam a Omnipotência de Deus. Entre estas, estavam duas dezenas de proposições de Tomás de Aquino.

Mas Aquino persistiu na interpretação da filosofia de Aristóteles como uma via racional que levaria a Deus, numa argumentação sólida e bem estruturada respaldada na solidez do corpus aristotélico. O princípio de todo o Universo, o Primum Mobile, era algo que Tomás de Aquino apontava como sendo o princípio primeiro nas suas cinco vias que provavam a existência de Deus. O dominicano raciocina baseado na ideia de causalidade para apresentar vias racionais (assumindo uma complementaridade entre Teologia e Filosofia) que levarão, necessariamente, à prova de que Deus existe. E Deus é, nessa perspectiva, a Primeira Causa Eficiente, o Ser Necessário incriado, em contraste com todos os seres possíveis. É o topo da hierarquia. Um dos elementos da filosofia aristotélica que influenciaram Aquino foi a distinção entre essência e existência (em Deus são uma só coisa; nas criaturas, a essência é a potencialidade para existir, enquanto a existência é o acto que a actualiza).

"A escolástica pressupõe antes de mais a aceitação da revelação, mas sem que isso signifique que daí se exclui a filosofia em favor de um domínio completo da teologia: a escolástica é ambas, aliás o próprio método por ela usado suscita necessariamente a filosofia. O que acontece é que as questões teológicas estão intimamente relacionadas com questões filosóficas ou, por outras palavras, o esforço de compreensão das primeiras implica necessariamente as segundas."
(escolástica na Infopédia [em linha]. Porto Editora. Disponível em https://www.infopedia.ptartigos/$escolastica,1 [visualizado em 2025-11-16 14:42:56].)

O pensamento de Aquino afirma-se, unanimemente, somente a partir do Concílio de Trento (1545-1563), no contexto da Contra-Reforma, sendo aí assumido como a base para a explicação da doutrina da Igreja Católica.

Em termos cosmológicos, a distinção entre um modelo "realista" e qualitativo (aristotélico) e um modelo "instrumentalista" ou quantitativo (ptolomaico), cada qual resultando de diferentes tradições textuais, foi enquadrado neste resumo de David C. Lindberg:

"One of the best ways of distinguishing medieval disciplines is to forget about their formal definitions and to examine them as textual traditions. The cosmological questions (...) tended to appear in commentaries on certain texts—Aristotle’s physical works (especially On the Heavens and Metaphysics), John of Sacrobosco’s Sphere, Peter Lombard’s Sentences, and the creation account in Genesis. The mathematical analysis of the heavens belonged to a different textual tradition, springing from Ptolemy’s Almagest and other works of mathematical astronomy produced during the Hellenistic period. Reinforcing this separation may have been the fact that the serious mathematical astronomer required esoteric mathematical skills that were out of reach for the average natural philosopher engaged in cosmological pursuits. During the early Middle Ages, the West was without access to the most important Greek sources of mathematical astronomy—the works of Hipparchus, Ptolemy, and others. Astronomy was certainly understood to be a mathematical art, a member of the mathematical quadrivium, but the amount of mathematical astronomy actually known to early medieval scholars was minimal. Authors such as Pliny, Martianus Capella, and Isidore of Seville offered an elementary description of the celestial sphere and its major circles; of the seven planets and their west-to-east motion through the band of the zodiac, including retrograde motion; and of the sun-linked movement of Mercury and Venus. The ability to deal with problems of chronology and the calendar was also a well-developed art. But knowledge of Ptolemaic models or any other scheme for the practice of serious mathematical astronomy was nonexistent." (The Beginnings of Western Science, (2nd. edition), Chicago: The University of Chicago Press, 2007, pp. 261-62)

No Islão surgiram traduções e comentários, também inovações e refinamentos matemáticos nascidos do estro dos seus autores, "aqueles para quem o céu é o tecto" (Al-Biruni, apud R. Hinckley Allen, Star Names..., 1899).

Quadrante astrolábico por Zayn al-Dīn (Shams al-Dīn) Muḥammad ibn Aḥmad al-Mizzī (m. 750 A.H./1349 A.D.), feito para Sulaymān ibn Muḥammad ibn Sulaymān em Damasco (The David Collection, Copenhagen, inv. no. 16/1988; fotógrafo: Pernille Klemp, in Sonja Brentjes (ed.), Routledge Handbook on the Sciences in Islamicate Societies Practices from the 2nd/8th to the 13th/19th Centuries, Routledge, 2023, p.600)

David A. King deu ênfase ao que chamou "...the Islamic aspects of Islamic science": "No Islão, como em nenhuma outra religião na história humana, o desempenho dos vários aspectos do ritual religioso tem sido auxiliado por procedimentos científicos. A organização do calendário, a regulação astronomicamene definida dos tempos das orações e a determinação da direcção sagrada da Kaaba em Meca - todos estes tópicos da ciência Islâmica tradicional continuam relevantes para os actuais crentes, e cada um deles tem uma história que recua a quase catorze séculos." (Science in the service of religion: the case of Islam, in: Impact of Science on Society, 159. Paris: U.N.E.S.C.O., 1990, p.245 [trad. nossa])

As cinco orações convencionais. As três nocturnas são reguladas por fenómenos do horizonte e do crepúsculo; as duas diurnas através dos comprimentos de sombras (King, 1990, Figure 3, p.250)

O Corão explicita na 10ª Surata: "Ele foi Quem originou o sol iluminador e a lua refletidora, e determinou as estações do ano, para que saibais o número dos anos e seus cômputos. Deus não criou isto senão com prudência; Ele elucida os versículos aos sensatos." (10:5, trad. Samir El Hayek). Na tradução de Helmi Nasr: "Ele é Quem fez do sol luminosidade, e da lua, luz, e determinou-lhe fases, para que saibais o número dos anos e o cômputo do tempo. Allah não criou isso senão com a verdade. Ele aclara os sinais a um povo que sabe."

O advento do Islão propiciou o desenvolvimento de uma astronomia "especializada" (mīqāt) aplicada às necessidades rituais (determinação da qibla, a direcção de Meca, determinação da primeira visibilidade do crescente lunar para conhecer o início dos meses do calendário, determinação das horas das orações diárias, etc.), agilizada por muwaqqits (os que "guardam o tempo"), astrónomos ao serviço das mesquitas. O calendário, todavia, passou a ser exclusivamente lunar e observacional, proibindo-se as intecalações e assim nunca sincronizado com as estações do ano. As interpretações mais tradicionalistas, que amiudadamente se impunham, somente aceitavam as tradições consideradas nativas (anwāʾ e manāzil), i.e. o sistema baseado nos nascimentos helíacos das estrelas como marcadores sazonais (que para além de calendárico era um um sistema de astrometeorologia) e o das mansões lunares, repudiando, oficialmente, qualquer veleidade astrológica (sendo que sempre existiram augúrios e práticas divinatórias populares paralelas).

Determinação do início dos meses: a teoria lunar ptolomaica manifestava razoável precisão em relação ao timings dos novilúnios e especificava o movimento da Lua em relação à eclíptica. Para prever a primeira visibilidade da Lua, é necessário descrever o seu movimento em relação ao Horizonte, o que exige o recurso a uma relativamente sofisticada astronomia esférica. (Gingerich, O., The Great Copernicus Chase and other adventures in astronomical history, Sky Publishing Corp., 1992, p. 47)

Julio Samsó (Islamic Astronomy, in Glick, T., Livesey, S. and Wallis, F., Op. cit. p.64), explica que os árabes pré-islâmicos utilizavam um calendário luni-solar e praticavam uma astronomia muito elementar, baseada nas fases lunares, no Sol, nascimentos helíacos de estrelas, etc. Em On both Sides of the Strait of Gibraltar..., Op. cit., 2020, pp.49-50, o mesmo autor salienta que esses povos estavam conscientes do calendário solar, observando a última estrela (raqīb) que se elevava no horizonte oriental antes do nascer do Sol no ponto em que este se elevaria; também observavam o ocaso acrónico (v. pág. Esfera) da estrela (naw') que tinha o seu ocaso a 180º. Estes pares de estrelas (raqīb e nawʾ) alteravam-se ao longo do ano enquanto os pontos do orto e do ocaso solares também se alteravam. O sistema dividia o ano em 27 períodos de 13 dias mais 1 de 13 dias (equivalendo a 365 dias = 1 ano). Acertava-se o calendário lunar e o solar intercalando um décimo terceiro mês lunar. Com a implantação do Islão, a intercalação foi suprimida pelo Profeta, que considerava que a tradição popular de relacionar as naw' com ciclos meteorógicos de chuvas e secas tinha conotações astrológicas ou facilmente se prestava a essas elucubrações. Cada novo mês começa obrigatoriamente com a primeira observação do crescente lunar, na sequência da chamada laylat al-shakk("noite da dúvida"), na transição para o novo mês. Entretanto, diversos expedientes matemáticos foram gizados para antecipar esse momento e conhecer a direcção do horizonte no qual a primeira visibilidade aconteceria. O meio do mês é logicamente assinalado pelo plenilúnio, al-badr.

A abordagem tradicional adaptada da época pré-islâmica continuou a ser a mais comum: Adapted primarily from pre-Islamic Arabia, folk astronomy flourished alongside mathematical astronomy over the centuries, but was far more widely known and practised. Even the legal scholars accepted it because of Kur’an, XVI, 16, ‘‘...and by the star[s] [men] shall be guided’’. There were four main applications of this traditional astronomical folklore: (1) the regulation of the Muslim lunar calendar; (2) the determination of the times of the five daily prayers, which are astronomically defined; (3) finding the kibla by non-mathematical procedures; and (4) the organisation of agricultural activities in the solar calendar. (King, David A., "Makka: as the centre of the world", in: The Encyclopaedia of Islam, 6, fac. 101-102, [pp. 180-187], Leiden: E.J. Brill, 1987; repr. in: Astronomy in the Service of Islam, Variorum Collected Studies Series; CS416, ch. X, p.7). A tradição original, não-matemática, baseava-se, portanto, apenas nos fenómenos observáveis, tais como os nascimentos (na tradição nativa, al-matla' era o ponto do horizonte onde se elevava um astro, geralmente uma estrela, importante na Anwa' e no sistema de mansões lunares), ocasos e passagens dos corpos celestes através da abóbada celeste, envolvendo também a associação destes a fenómenos meteorológicos. Assumiu como objectivos primordiais a regulação do Calendário Muçulmano e do timing das orações, a determinação da kibla (ou qibla, a direcção de Meca) através de métodos expeditos não matemáticos e ainda a organização das actividades económicas, nomeadamente a agricultura e a pastorícia, em função do ano sazonal.

As direcções da kibla (palavra que, segundo King, parece estar relacionada com "kabul", o vento de Leste) eram expressas através dos nomes dos ventos, das regiões envolventes (Síria, Iémen, etc.) e das direcções cardeais. Antecedendo o próprio Islão, a Ka'ba assumirá um papel fulcral na nova religião, enquanto axis mundi e imago mundi. Segundo a lenda, foi construída por Abraão (Ibrahim) e o filho Ismael (Ismāʻīl) segundo um paradigma celeste: al-bayt al-ma'mur (o protótipo da Ka'ba, situado acima desta no "Sétimo Céu" e "continuamente visitada pelos anjos", como mencionado na Surata 52:4).

Faces, ângulos e até diferentes segmentos da Ka'ba foram pois associados às direcções, ao ventos, às diferentes regiões do Mundo Islâmico, etc. O jurista (faqīh) Muhammad Ibn Surāqa al-‘Amiri (de origem iemenita, m. 1019 A.D.) está ligado ao desenvolvimento desta "geografia sagrada". Um esquema por si gizado, de oito sectores (definidos pelas direcções cardeais e pelos pontos do horizonte tocados pelo sol nos dois dias dos solstícios), foi divulgado por Ibn Rahik e refinado por Ibn al-Adjdabi. Outro esquema similar encontra-se, por exemplo, em escritos do egípcio al-Dimyati (séc. XII) ou em al-Fārisī (Adém, circa 1275). Os sectores estavam associados às faces e aos ângulos da Ka'ba. Outros esquemas incluíam onze ou doze sectores. Alguns esquemas mais tardios apenas grafavam os nomes das localidades em torno a Ka'ba, sem incluir qualquer informação explicativa acerca das respectivas qiblas. São exemplos os de autores como Yāqūt al-Rūmī (ca. 1225), al-Qazwīnī (circa 1250), bem como al-Ṣafāqusī (circa 1550), num belo esquema colorido incluído no seu atlas de navegação. Os esquemas foram copiados e utilizados até ao séc. XIX.

A orientação da base rectangular da Ka'ba na direcção do nascimento da estrela Canopus (designação indígena: Suhel ou Suhail, estrela associada à direcção sul, janūb; α Carinae na designação de Bayer) e do orto e ocaso do Sol no solstício de Verão, segundo diversas fontes medievais (King, "Science in the service of religion: the case of Islam", in: Impact of Science on Society, Op. cit., p.254, Fig. 6). "Shamal" e "Janub" referem-se comummente ao norte e ao sul, respectivamente (todavia, a orientação do edifício está afastada 30º desse eixo); à direita: ilustração de esquema de 8 direcções, identificando diferentes regiões geográficas em redor da Ka'ba (MS Şehit Ali Paşa 2776,2, fol. 56v, Biblioteca Süleymaniye, Istambul)

Era uma geografia sagrada integradora, na qual uma direcção, uma das faces ou um ângulo da Ka'ba, um vento, uma época do ano ou uma região geográfica eram sinónimos, (e.g., o horizonte sul, janūb, al-Yaman [o Iémen], nome da face sudeste da Ka'ba). Atentemos neste excerto de Ibn al-Ajdābī, circa 1225 (King, Sacred Geography & Qibla Sources, J. W. Goethe Univ., Frankfurt, 2019, p.21):

“In the Eastern sector to the South of the parallel of Mecca the qibla is towards summer sunset and what is close to this, which is (the direction) facing the wall of the Kaʿba going from the Yemeni Corner to the Black Corner (that is, the Eastern corner with the Black Stone). The localities in this sector are the Eastern parts of the Yemen, al-Shiḥr, India, and the parts of Southern China beyond.”

Vários métodos matemáticos aproximados (um dos quais atribuído, erradamente, a al-Battani) foram entretanto utilizados. As mesquitas eram tradicionalmente orientadas para Meca, segundo as técnicas disponíveis nessa época.

Os estudos de mesquitas históricas que têm em consideração a moderna tecnologia disponível (e.g., Gibson, Early Islamic Qiblas: A Survey of mosques built between 1AH/622 C.E. and 263 AH/876 C.E., Independent Scholars Press, 2017; Deus, A. J., Monuments of Jihad - The Thought Process of Determining Qibla Orientations by Turks, 2018) radicam, segundo King, num erro basilar: utilizam a direcção geográfica moderna de Meca e não a que podia ser determinada no passado, há 8, 9, 10 ou 11 séculos (King, Islamic sacred geography for finding the qibla by the sun and stars, 2019, Appendix.)

A abordagem científica, respaldada nos contributos estrangeiros, na Matemática e na Geometria, levantava eventuais desconfianças e intolerância. Segundo o legalista iemenita al-Asbahi (séc. XIII): "Os astrónomos retiraram o seu conhecimento de Euclides, [dos autores do] Sindhind, Aristóteles e outros filósofos, e todos eles eram infiéis." (MS. Cairo Dar al-Kutub, mikat 984, 1, fol. 6a-b). Mas nem por isso se deixou de verificar um notável florescimento científico em determinadas épocas e contextos.

A ciência Islâmica é multicultural e desenvolve-se em contextos étnicos, culturais e até linguísticos diversificados (daí a actual utilização académica do termo "Islamicate" para acentuar toda a diversidade que se abriga na umbrela da influência religiosa prevalecente). Revela influências gregas, persas e indianas (neste último caso particularmente na tradição das tabelas astronómicas [zij; pl. zijes ou zĩjãt] e na utilização dos numerais depois chamados "indo-arábicos", num cómodo sistema posicional onde a posição do algarismo no número modifica o seu valor). A Astronomia distingue-se, antes de mais, por uma preocupação com a consistência física dos modelos e com a relação entre estes modelos e a observação (Morrison, R., Islamic Astronomy, in: Lindberg, D. and Shank, M., Op. cit., p.109 et seq.).

Num testemunho da proficiência matemática, verifica-se o tratamento de funções trigonométricas como quantidades algébricas manipuláveis através de fórmulas, não apenas enquanto linhas geométricas.

A tradição indo-iraniana, com origem grega pré-ptolomaica (nomes de diversos tratados indianos denunciam a proveniência mediterrânica) começou a penetrar terras Islâmicas no período Omíada (a partir de c. 679), com grande desenvolvimento durante o califado de al-Mansur (754–775). Durante o califado de al-Ma‘mun (813–833) dá-se um ponto de viragem com a introdução da astronomia ptolomaica e a tradução do respectivo corpus. A civilização Islâmica produziu traduções, comentários, astrolábios, tabelas com os respectivos cânones explicativos e desenvolvimentos matemáticos, nomeadamente o aperfeiçoamento dos métodos numéricos, um antigo e difícil desafio. Alguns dos nomes das estrelas que hoje utilizamos estavam gravados nos astrolábios, designações provenientes da tradição erudita (que por norma prevaleceu sobre a autóctone nomenclatura beduína), traduzidos do catálogo de Ptolomeu. É da tradução dos textos clássicos pela intermediação árabe e dos contributos dos autores Islâmicos coevos, inicialmente a partir da Península Ibérica, que o conhecimento alimentará a Europa, por exemplo através da influente tradução do Almagesto por Gerardo de Cremona em 1175.

Segundo P. Kunitzsch, quase todas as zijes (manuais com tabelas que incluíam os cânones ou regras) usavam coordenadas eclípticas (mormente a longitude), extraídas do Almagesto, e acrescentavam uma correcção (uma constante de precessão) às longitudes das estrelas, dependendo da sua data ("epoch", como actualmente dizemos). Para além da precessão, muitos astrónomos levaram em consideração a chamada trepidação (v. infra). O valor da precessão "original" (i.e. a que Ptolomeu convencionou no Almagesto) era de 1º = 100 anos. Al-Biruni, por exemplo, usou a correcção [valor de Ptolomeu] + 11° e 10', para o ano equivalente a 880 A.D. (utilizando um valor constante de precessão corrigido pelos astrónomos Islâmicos: 1º = 66 anos). Ou seja, acrescentou 11;10º (11º e 10') à longitude "ptolomaica" de cada estrela. Raramente se construíam novas tabelas pela observação independente, tanto no Oriente como na Europa medieval. Como exemplos excepcionais, observações concretas estão na base da Zij al-Mumtahan (Lat. Tabulae Probatae, i.e. "tabelas testadas"), sob o patrocínio do califa Al-Maʾmūn, também o influente catálogo de Abd al-Raḥmān al-Sūfī. Mas geralmente corrigiam-se as longitudes numa tabela pretérita, sendo o catálogo de Ptolomeu (que no contexto Latino é o da tradução de Gerardo de Cremona) "matriz" privilegiada. Qualquer tabela que resultasse da observação seria mais tarde privilegiado enquanto base para a construção de ulteriores tabelas. (vide Kunitzsch, Paul, "Star Catalogues and Star Tables in Mediaeval Oriental and European Astronomy", Indian Journal of History of Science, 21, New Delhi, 1986, pp.113-22; repr. in: The Arabs and the Stars : Texts and Traditions on the Fixed Stars, and their Influence in Medieval Europe (Variorum Collected Studies), Routledge, 2016 [1989]).

As que maior circulação tiveram na Europa foram as Tábuas Afonsinas (i.e. "Alfonsinas", de Alfonso X, el Sabio), gizadas por astrónomos judeus e árabes. Na realidade desconhece-se actualmente qualquer versão castelhana. Somente os cânones (instruções), v. edição de Rico y Sinobas, Tomo IV (Madrid, 1866). III-83: "Libro que a por nombre el de las taulas Alfonsies". Na forma que podemos documentar actualmente, trata-se de uma colecção de tabelas planetárias e outras, em Latim, compiladas (em circunstâncias que não são bem conhecidas) em Paris nos anos de 1320. Sumamente influentes ao longo de três séculos, as tabelas surgem nessa elaboração "Parisina" por iniciativa (tanto quanto se sabe) de Jean de Murs, Jean de Lignères e Jean de Saxe (John Danko, Johannes de Saxonia). Emmanuel Poulle ("The Alfonsine Tables and Alfonso X of Castile", Journal for the History of Astronomy, 19 (1988), 97-113) argumentou que as tabelas que conhecemos como "Alfonsinas" se originaram em Paris por volta de 1327, pouca relação tendo com os astrónomos ibéricos. Para uma argumentação favorável ao carácter derivativo e uma crítica arguta dos argumentos de Poulle, v. John David North: Just whose were the Alfonsine Tables (in: From Baghdad to Barcelona. Studies in the Islamic Exact Sciences in Honour of Prof. Juan Vernet", Barcelona, 1996, pp.453-475). Os antecedentes ibéricos, nomeadamente toledanos parecem difíceis de ignorar mas as tabelas "originais" de Afonso X permanecem um "fantasma". Como Philipp Nothaft judiciosamente afirma: "(...) the idea that the Latin or “Parisian” Alfonsine Tables were the outcome of some process of adaptation carried out in Paris has the appearance of a dogma, whose justification is never provided." (Nothaft, C. P. E. (2023). A new series on Alfonsine astronomy. Journal for the History of Astronomy, 54(1), 113-118.). Serão , como Poulle defendia, pseudo-epigráficas? Nothaft refere esse "veritable elephant in the room" no estudo da Astronomia Medieval. Para uns estão na base das Parisienses, para Poulle (como vimos) nunca existiram, para Samsó (On Both Sides of the Strait of Gibraltar, 2020) as ulteriores tabelas estão (em diversas peculiaridades, como os parâmetros dos movimentos médios) inegavelmente ligadas à tradição do al-Andalus e podem ter existido dois "sets" diferentes. O debate continua.

A disseminação das edições de Paris foi notável. Os cânones explicativos de João de Saxónia foram compostos em 1327 e servirão de base à editio princeps (por E. Ratdolt, 1483). As Tábuas parisienses usavam o dia como base para as suas tabelas do motus médio dos planetas, facilmente adaptadas aos calendários (Juliano, Islâmico e Hebraico) usados em diferentes contextos culturais. Em resumo, quando falamos destas tabelas referimo-nos às declarações, regras ou cânones e às numerosas e sucessivas edições acrescentadas das tabelas numéricas latinas de Paris. Poulle salienta a sua relevância histórica:

"Dans le domaine de l'histoire des sciences, d'autre part, elles définissent, entre l'astronomie des tables de Tolède, en vigueur au X.me siècle, et celle de Copernic, une période intermédiaire bien précise pendant laquelle les astronomes ont rendu au géocentrisme sa conséquence logique: la préférence donnée à l'année tropique sur l'année sidérale." (Les tables alphonsines et Alphonse X de Castille. in: Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres, 131ᵉ année, N. 1, 1987. pp. 82-102;p. 86).

Estas tabelas adoptam a Nona esfera e as coordenadas tropicais (medidas do ponto vernal, lugar do Equinócio de Primavera no Hemisfério Norte), votanto à obsolescência as tabelas anteriores, ainda baseadas na Oitava esfera e nas coordenadas siderais (das estrelas concretas).

N.B.: O valor da correcção das longitudes siderais adoptado no catálogo alfonsino de estrelas dos Libros de la ochava espera, bem como em algumas edições impressas das tabelas.era = Valor de Ptolomeu + 17;08º (17º e 8')

As sucintas tabelas com listas de estrelas para utilização no astrolábio (também úteis para outros instrumentos, e.g., quadrantes, globos celestes), introduzidas na Europa a partir de traduções de exemplares árabes, foram importantes tanto na transmissão de aspectos técnicos como na de vocabulário específico, por exemplo a nomenclatura das estrelas. Segundo Paul Kunitzsch (Op. cit., 1986, p.119), a mais antiga no contexto latino foi uma lista com 27 estrelas, datável de finais do séc. X. Uma das suas coordenadas era a mediatio coeli (i.e., o grau da Eclíptica que culminava simultaneamente com a respectiva estrela).

Para os astrónomos islâmicos, Arin era o meridiano de referência: "Arin, de uma distorção no Árabe ('ryn, em vez de 'zyn = Uzayn), do nome da cidade indiana de Ujjayini. Parte da astronomia árabe-islâmica foi inspirada por textos indianos bem cedo traduzidos na corte dos califas em Baghdad. Daí Ujjayini enquanto lugar no centro do mundo, no meridiano zero e no equador, penetrou nos textos astronómicos e geográficos árabes, sendo ulteriormente transmitida ao ocidente medieval." (Kunitzch, P., On the Authenticity of the Treatise on the Composition and Use of the Astrolabe Ascribed to Messahalla, Archives Internationales d'Histoire des Sciences, 31. Wiesbaden, 1981, p.58, n.70 [trad. nossa]). Ou seja, trata-se do primeiro meridiano dos astrónomos indianos. Segundo North (Chaucer's Universe, Op. cit., 1988, p.160), algumas listas geográficas latinas referiram Arin [ou Aryn] como tendo latitude nula e uma longitude de 90º "do Oeste". Na tribulação das traduções, o lugar também foi pontualmente confundido com o próprio "centro da Terra", ou seja, do Universo (enquanto referência idealizada, convencional).

Em questões cronológicas, J. Samsó sublinha (Islamic Astronomy, Op. cit., p.54) que a utilização de determinadas eras cronológicas se revestia de uma lógica astronómica. A Era de Nabonassar era a mais citada no Almagesto de Ptolomeu, onde também se encontram as de Filipe (i.e., Phillipus III Arrhideus, meio-irmão de Alexandre Magno, aparentemente usada apenas para fins astronómicos e com uma variante na historiografia árabe [v. também Hallo, William W., "The Concept of Eras from Nabonassar to Seleucus", Journal of the Ancient Near Eastern Society, 16 (1), 1984] e as dos imperadores Augusto, Adriano e Antonino. Nas "tabelas manuais" de Teão (Θέων, Theon) encontra-se principalmente a de Filipe (e o Calendário Egípcio), mas a Era de Diocleciano também é mencionada. Al-Battānī, na sua zīj (manual de tabelas e cânones) utiliza as de Filipe, Alexandre, a Hijra (Hégira) islâmica e a de Yazdijird (de origem persa). A Era do Dilúvio é curiosamente inserida no contexto indo-iraniano das tabelas de al-Khwārizmī pois corresponde, por coincidência, com o início de um ciclo hindu (o Kaliyuga, no ano -3101), v., por exemplo, D. Pingree, "History of Mathematical Astronomy in India", in: Dictionary of Scientific Biography, XV, New York, 1978, p.555.

Ilustração do modelo planetário ptolomaico utilizando orbes (Nasir al-Din al-Tusi’s al-Tadhkira fi ‘ilm al-hay’a. - Staatsbibliothek, Berlin, MS. Or. oct. 3568, detalhe fol. 17a - CC BY‑SA 4.0)

Embora hoje "politicamente incorrecta", a opinião de A. Pannekoek tem, no longo prazo, fundamento: a Astronomia no contexto Islâmico almejou somente a verificação e optimização do trabalho dos seus predecessores; teoricamente não foi além dos veteres antiqui e quando divergiu de Ptolomeu, foi quase sempre para retornar a Aristóteles. (A History of Astronomy, Dover Publications, 1989 (1961), pp. 169-170). Sendo matemáticos extremamente dotados e tendo assimilado técnicas indianas, promoveram importantes contributos, desde a introdução dos numerais "indo-arábicos" até à substituição do cálculo das cordas de Ptolomeu pelo dos senos da Trigonometria (as Tabulae Sinuum, tabelas de cordas e arcos, utilizadas desde então). Mas os interesses e contributos foram principalmente observacionais e descritivos (as suas zijes foram extremamente influentes) e a especulação cosmológica ocupava um lugar inconspícuo. Houve, todavia, elucubrações no âmbito da chamada "hayʾa" (num dos sentidos em que a palavra foi utilizada, e.g., pelos aristotélicos do Islão quando se referiam a um eventual universo físico não-ptolomaico, v. Samsó, Op. cit., 2020, p.499). E a influência pode, discute-se, ter sido obliquamente decisiva sobre Copernicus. Mas não se lhes deve, na substância, o salto qualitativo a que se assistiu mais tarde através da "Nova Astronomia". Depois de uma época dourada (séculos IX-XIII), com extraordinários conseguimentos, a ciência em terras islâmicas cedo estiolou sob a pressão da ortodoxia religiosa (que se manifestava assiduamente, por "vagas") e do pesado conservadorismo, análogo ao que encontramos na literatura patrística dos primeiros séculos do Cristianismo. Os célebres observatórios foram (invariavelmente) efémeros e o debate de ideias condicionado por um ambiente teocrático pouco estimulante, pois tudo o que era importante já havia sido revelado e devidamente explicado, não admitindo a exegese.

Como exemplo dos equívocos "woke" repetidos nas actuais "Histórias" do Método Científico, lemos uma pertinente crítica de Thony Christie (The Renaissance Mathematicus), na sua "review" de um título de David B. Teplow. Este último descreve a ênfase 'experimental' de Roger Bacon (c.1220-1292), afirmando que Bacon aprendeu tudo com os alunos de "Spanish Moors" e que o método experimental não começou na Europa: "It is absolutely wrong to assume that experimental method was formulated in Europe. Roger Bacon, who, in the west is known as the originator of experimental method, had himself received his training from the pupils of Spanish Moors, and had learnt everything from Muslim sources. The influence of Ibn al-Haitham on Roger Bacon is clearly visible in his works." Christie comenta este dislate: "To find this ahistorical garbage in a serious book is to say the least stunning. That Roger Bacon was the first European to write about and propagate the optics of al-Haytham is true but that he had received his training from the pupils of Spanish Moors, and had learnt everything from Muslim sources, is total cobblers."

Na tradicional perspectiva que que enfatiza o importante papel intermediário da ciência escrita em Árabe, que veiculou (refinando e, eventualmente "baralhando") muito do saber da Antiguidade, um vasto acervo de ecléticos textos foi traduzido e recebido com fervor na latinidade, sugerindo um léxico e práticas estimulantes, também no que diz respeito à Astrologia:

"The system of Abu Ma‘shar and other Arabic astrologers seems to be an amalgam of older traditions, and this it was that passed into Latin astrology. It was really late Greek astrology, from the first four or five centuries of our era, coloured by its passage through Persian and, to a lesser extent, Indian hands, which most filled the minds of the medieval astrologers, and only rather less the restrained art of Ptolemy’s Tetrabiblos. Not only were they attracted by all the new and strange Arabic terms — they revelled in hylegs rather than ‘prorogators’ and so forth — and also by the fashionable names, but the differences in emphasis may have made the Arabs’ astrology more exciting." (Tester, p.168).

O artisticamente refinadíssimo horóscopo da natividade do sultão Iskandar, datável de 1384 e elaborado no início do séc. XV (Kitab-i viladat-i Iskandar. The Wellcome Institute, Wellcome Collection - WMS Persian 474)

O notável florescimento da Astrologia no Islão é uma questão curiosa. Como Peter Whitfield alvitra, talvez a doutrina da 'Unicidade de Deus' (tawhid), da qual se deduz a da unicidade da sabedoria, explique porque é que uma religião "revelada", ainda mais severa e avessa a "compromissos" do que o Cristianismo, pode aceitar uma filosofia "pagã" da Natureza, como era a Astrologia. (Astrology: a History, Op. cit., 2001, p.81). Esta floresceu sob a dinastia Abássida, pois o espírito da época, através do movimento "Mu’tazilah" estava aberto a uma interpretação do mundo que defendia o primado da 'razão'. E chegou também ao ocidente do império. Ulteriormente, manifestar-se-á uma resistência e mesmo uma declarada oposição à intromissão na religião do racionalismo pagão. A partir do século XIII, a astrologia no Islão estará moribunda, declinando consideravelmente sob o impacto de restrições de origem religiosa e filosófica. (ibid., p.94). Os mais influentes autores e respectivos tratados são anteriores. Curiosamente, é a partir desta mesma época que as suas traduções influenciarão consideravelmente as práticas no Ocidente Latino.

É inegável que a tradição astronómica das regiões islamizadas (‛ilm al-hay’a, "conhecimento da estrutura/configuração" [do universo], ilm al-falak, "conhecimento da esfera celeste" e ‘ilm al-nuj¯um, "conhecimento das estrelas", aplicável tanto à astrologia como à astronomia) se revelou riquíssima nos intercâmbios e nos refinamentos (teóricos e práticos). Mas foi efémera. Por diversos motivos (sociais e religiosos) estiolou após o magnífico período entre os séculos IX-XIII (aproximadamente). Também os seus importantes observatórios (sendo o de Ulugh Beg, em Samarcanda, um exemplo paradigmático) tiveram escassa longevidade. Como se pode constatar pelas datas, as grandes referências são antigas. Todavia, ainda encontramos alguns notáveis astrónomos depois da época de al-Tusi (1201-1274), como Sadr al-Sharia al-Bukhari (c. 1347) ou Ibn al-Shatir (c. 1375). No séc. XV destaca-se o mencionado Ulugh Beg e o seu catálogo de estrelas independente (i.e. resultante de observações convretas e não de simples actualização de coordenadas, como era habitual).

Sábios judeus sefarditas perpetuaram a tradição das tabelas e dos almanaques, sendo o Almanach Perpetuum baseado em tabelas do Ha-Hibbur ha-gadol ("Grande Composição") de Zacuto (Tabulae tabularum coelestium motuum sive Almanach Perpetuum) exemplo da transição do manuscrito para a imprensa. (v. Chabás, J. & Goldstein, B. R., Astronomy in the Iberian peninsula: Abraham Zacut and the transition from manuscript to print, Transactions of the American Philosophical Society. Philadelphia, 2000.). Os cânones foram pubicados em Castelhano, supostamente por um judeu português: José Vizinho. Em Árabe documentam-se pelo menos três traduções do Almanach, popular do Magrebe (Maghrib) ao Iémen (al-Yaman) entre os séculos XVI e XIX (!), o que é revelador de um contexto que não evoluiu.

Entretanto, o sincrético "modelo" ptolomaico-aristotélico que temos acompanhado é enquadrado através da interpretação escolástica na mundividência Cristã, consequentemente na sua explicação da "Máquina do Mundo", como mais tarde exposta pelo génio de Camões, quando Tétis a descreve ao Gama:

A observação era "programaticamente" preterida relativamente à inferência e razão da lógica aristotélica. A Esfera Universal dividia-se num coração central constituído pelos quatro elementos e pelas esferas etéreas dos corpos celestes. O mundo sublunar assiste à corrupção e ao devir. As esferas planetárias são constituídas por um "éter" incorruptível e eterno, invariáveis na sua substância. O conjunto traduz-se numa organização hierarquizada, completa, imponente e inteligível. C. S. Lewis faz-nos experienciar o "modelo" pretérito, em contraste com o contemporâneo:

...Hence to look out on the night sky with modern eyes is like looking out over a sea that fades away into mist, or looking about one in a trackless forest-trees forever and no horizon. To look up at the towering medieval universe is much more like looking at a great building. The 'space' of modem astronomy may arouse terror, or bewilderment or vague reverie; the spheres of the old present us with an object in which the mind can rest, overwhelming in its greatness but satisfying in its harmony (Lewis, C.S., The Discarded Image, Op cit, p.99).

Para desfrutar do sistema na sua maturidade tardo-medieval e renascentista, guiamo-nos pelo clássico de Luciano Pereira da Silva (A Astronomia de Os Lusíadas; páginas assinaladas são da reedição de 1972):

"[Agilizou-se] a sobreposição de movimentos periódicos da forma mais simples, isto é, de movimentos circulares e uniformes. Os mais complicados movimentos celestes foram, dentro dos limites de precisão que permitiam atingir os instrumentos de observação à vista desarmada, representados com grande felicidade e sucesso pela aplicação daquele pensamento matemático. Os planetas movem-se em círculos (epiciclos) cujos centros se deslocam sobre outros círculos (deferentes) excêntricos em relação à Terra, colocada no centro do Mundo, resultando da combinação daqueles movimentos as suas estações e retrogradações. (p.71) (...) O sistema satisfaz os votos dos astrónomos ansiosos de cânones para o cálculo de tábuas de posições exactas dos planetas, tábuas que a observação confirme dentro dos limites dos erros dos instrumentos. Mas descontenta os adeptos intransigentes da Física peripatética [de Aristóteles], cujos princípios julgam ameaçados pelo autor da Magna Sintaxe [Ptolomeu]. (...) [Todavia] as várias rotações sobre epiciclos e deferentes são, segundo ele [Ptolomeu], puros artifícios de cálculo, e o único princípio que deve guiar o astrónomo na escolha das hipóteses é o da maior simplicidade. Mas não deve hesitar-se em juntar combinações mais complexas sempre que seja preciso para salvar as aparências, isto é, para levar a coincidirem as posições calculadas dos astros com as posições observadas com os instrumentos." (p.73).

"Purbáquio, nas suas Teóricas, adoptou as esferas sólidas dos árabes [que na verdade recuam à Antiguidade], feitas de quinta-essência, [rigorosamente] com as dimensões suficientes para, dentro delas, terem livre jogo os deferentes e epiciclos de cada planeta. O modelo criado para a concepção do Universo deixa, pois, de ser puramente geométrico; é um modelo físico-mecânico. É a máquina do Mundo, que ao Gama e companheiros é dado ver com os olhos corporais." (ibid., p.79).

Purbáquio (Georg von Peuerbach, Lat. Purbachius) foi o primeiro, no Ocidente, a expender de modo completo a teoria dos epiciclos, inserindo-a nas esferas aristotélicas e separando a região de cada planeta recorrendo a esferas sólidas. Gizou um célebre epítome, publicado em 1454, com as teorias planetárias apresentadas de modo coerente e integrado, que combinavam habilmente a exposição básica dos excêntricos e epiciclos de Ptolomeu com as "esferas cristalinas" e sólidas de Aristóteles, contíguas entre si. Criou um mecanismo "ajustado" que, como Arthur Berry referiu, de certo modo "escavou" e "tornou ocas as esferas cristalinas de Aristóteles de modo a criar espaço para os epiciclos de Ptolomeu".

Para uma resenha histórica da vetusta controvérsia (antiga e medieval) acerca da existência concreta das esferas, v. Pierre Duhem, Le Systeme du monde (Paris, 1913-17), Vol. II, Pt. I, chs. x-xi; Vol. IV, Pt. II, chs. viii-ix, et passim.

A "Esfera do Sol" [i.e. o aparato dos componentes da órbita do Sol] nas Theoricae de Georg von Peuerbach. Constituída por três "orbes" ou "céus" (o deferente do Sol e dois deferentes dos auges do Sol), é um dos exemplos mais simples. O círculo menor (interior) é o lugar dos planetas interiores. Aqui se situam o centro da Terra, ie, do Mundo (A) e o centro dos excêntricos e, consequentemente, da órbita do deferente do Sol (B). A negro, os dois deferentes do auge do Sol (E e F); o anel branco é o deferente do Sol (como se confinado entre duas "paredes", uma côncava e outra convexa), por onde corre o círculo CGD, com centro em B, obviamente excêntrico em relação ao centro do Mundo, percorrido pelo centro do Sol (G) no seu percurso anual pela Eclíptica. O ponto C assinala o auge (o ponto da órbita mais próximo da 8ª Esfera), D assinala o oppositum augis, ponto mais próximo da Terra, onde a velocidade é maior. São, respectivamente, o apogeu e o perigeu (Theoricae nouæ planetarum : id est, septem errantium syderum, id est, septem..., 1534)

O célebre Tratado da Esfera (c.1230) de Sacrobosco que, como Giles E. Gasper refere, era informado pela complexa herança dos comentários e críticas árabes (escritos a partir do séc. VIII) ao corpus ptolomaico, que só chegou mais tarde à Europa, foi mais tarde traduzido "em lingoagem" (i.e., no vernacular) e anotado por Pedro Nunes (1502-1578), resumindo a perspectiva geocêntrica e fazendo algumas adendas. Nunes escreveu um epítome a versão "definitiva" do sistema (que contemplava dez Esferas, sem contar com o supremo Caelum Empyreum, o undécimo céu resplandecente e invisível dos teólogos). No que diz respeito às chamadas "estrelas fixas" (no ceo oytauo ou 'Oitava Esfera'):

"Chamãsse fixas porque estão sempre em hũa mesma distancia de nos por estarẽ todas ẽ hũ soo ceo q he o oytauo: o qual per razam dellas se chama firmamento & amostrãsenos estas estrellas sempre per hũas mesmas figuras & guardã o mesmo sitio as quaes cousas nã ha nos planetas. E segũdo a comũ escola dos astrologos a nona esphera não he primeiro mobile mas segundo & ho decimo he ho primeiro: & nestes dous ceos de cima nã ha estrellas & por tanto não se comprehende pello sentido [i.e., não se vê directamente] se não per razã porque experimentamos os seus mouimentos na .8. que não sam proprios a ella." [Ou seja, infere-se a realidade das referidas esferas pelo efeitos indirectamente percebidos nas esferas inferiores, nomeadamente na 8ª.]

Rheticus (Georg Joachim, 1514-1574), na Narratio prima (uma apresentação sucinta do sistema de Copernicus) refere o "orbem stellarum, quem octavum vulgo appellamus..."

No desenho prevalecente, o Oitavo céu (o "Aplanes" dos gregos) era, portanto, o das estrelas fixas. O Nono céu, característico pela sua diafanidade, era chamado "Aqueo" ou "Cristalino". Não tinha estrelas. Considerava-se que estavam aí as arcaicas Águas Superiores mencionadas no Genesis: "Benedicite aquae quae super caelos sunt..." (trecho do cântico bíblico e litúrgico chamado Benedicite ou "Cântico das Três Crianças"). Para alguns autores mais antigos, aí teriam sido guardadas as águas para a inundação do Dilúvio Universal. Para outros, com enfoque mais cosmológico, serviam para arrefecer os céus, temperando o calor ígneo gerado pelo incessante e uniforme movimento dos céus e das estrelas. O seu movimento próprio (a Precessão dos Equinócios) era de 1 grau em cada 100 anos, segundo a opinião de Ptolomeu, de ocidente para oriente, pela ordem dos signos (Aries, Taurus,...). Para Pedro Nunes, seguindo a tendência renascentista, este movimento pertenceria à nona esfera e seria de 1 grau e 28 minutos em cada 200 anos, de modo que em 49 mil anos se cumpria a revolução. E o movimento próprio da Oitava era o da chamada "trepidação" (v. infra) que se faria em 7.000 anos.

Quanto à cinemática deste complexo modelo, no qual cada esfera recebe os movimentos das superiores e manifesta ainda um movimento próprio, reza o texto de Sacrobosco:

"Mas o primeiro mouimento moue & leua com seu ympeto todallas outras Spheras & em hũ dia cõ sua noite fazẽ per derredor da terra hũa reuolução [trata-se do movimento diurno de 24 horas, d'o ceo volubil com perpetua roda (Os Lusíadas, VII, 60)]. E porem ellas sem embargo deste mouimento: andão em contrayro. A oytaua Sphera em cem annos hum grao [a Precessão, segundo Ptolomeu]: & a este segundo mouimento parte per meo ho zodiaco, debaixo do qual cada hũ dos pranetas [planetas] tem propria sphera: em a qual anda per proprio mouimento: contra o [no sentido contrário ao] mouimento do derradeyro ceo [i.e., do Primum Mobile]: & em diuersos espaços de tempos fazem suas reuoluções. Saturno em .30. annos: Jupiter em .12. Mars em dous. Sol em .365. dias: & quasi seys oras. Venus & Mercurio quasi em outro tanto tempo, a Lua em vinte & sete dias & oyto oras."

Ou seja, o céu das estrelas fixas possui, nesta interpretação, dois movimentos (o Diurno e o de Precessão). Mas Pedro Nunes adverte:

"Isto segundo a opinião de ptolomeu porque os astrologos que depoys forã [i.e., mais recentes] acharam que este mouimẽto de occidẽte pera oriẽte pella ordẽ dos signos pertence a nona esphera: & que nã he em cem ãnos hũ grao mas em 200. hũ grao & .28. minutos de sorte que ẽ 49. mil ãnos falando naturalmẽte se cõprira sua reuolução. E o mouimento proprio a oitaua he o da trepidação que se faz em .7000. annos."

Atribui-se doravante o movimento de precessão (cujo valor difere do ptolomaico) à Nona, deixando a Oitava com um estranho movimento próprio, resultante de uma teoria de inspiração árabe e comummente aceite na época de Nunes: a trepidação ("titubatio").

O converso alemão Paulus Ricius, no séc. XVI, terá relacionado estes períodos com números bíblicos, nomeadamente com o ano sabático, aqui "amplificado" (7000x7000=49000). E Pedro Nunes adopta este valor precessional mais recente de 1º e 28' a cada 200 anos. Anteriormente, Sacrobosco ou Dante limitaram-se a seguir Ptolomeu (1º=100 anos), enquanto al-Battani (conhecido entre nós como Albaténio, c. 858–929), suficientemente lúcido para renunciar à fantasia da trepidação, chegou, por suposta comparação com valores atribuídos às observações de Menelaus de Alexandria (documentadas no Almagesto), a um valor de 1º em 66 anos, muito próximo da realidade da Precessão. Mas foi uma admirável excepção. Copernicus ainda levou a "trepidação" muito a sério no De Revolutionibus.

Accessus et Recessus- a Trepidação

"The ninth-century Arabs could not determine the precession rate with any exactness from their own measurements alone. The only hope lay in a comparison with the data handed down by Ptolemy. The straight line connecting Ptolemy's observation of A.D. 139 with the cluster of Arabic observations has a slope of 1° in 65 years. But the slope of the line connecting Ptolemy' s observation with Hipparchus's is 1° in 100 years. It therefore looked as if the precession rate had increased since the days of the Greeks. Actually, the rate had been constant at 1° in 72 years during the whole period, and the apparent variation was due solely to errors of observation. If the Arabs had ignored Ptolemy and simply calculated the precession between Hipparchus's time and their own, they would have obtained a rate very close to the true one. But of course they had no way of knowing this." (The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p.275)

Vários modelos surgiram ao longo dos séculos. Azarquiel (al-Zarqālī, al-Zarqālluh), séc. XI, discutiu três e adoptou o que se tornou 'convencional'. Foi principalmente divulgada pelo tratado De motu octave spere, tradução latina de um original árabe desaparecido. Raymond Mercier defende que a solução, como se infere das tabelas do mencionado tratado, foi concebida para funcionar especificamente com as Tábuas Toledanas e qualquer atribuição anterior ao séc. XI (Thābit ibn Qurra, a quem se atribuía o tratado, vivera quase dois séculos antes) está, afirma, fora de questão. ("Accession and Recession: Reconstruction of the Parameters", in: From Baghdad to Barcelona..., Op. cit., 1996, vol. I, p.299). Na astronomia "Alfonsina", o cálculo da diferença entre coordenadas siderais e tropicais (pois era disso que se tratava) associava essa oscilação com a mais "tradicional" componente linear (a segunda seria anual, a primeira periódica). Assim, nas disseminadas tabelas "parisinas", optou-se por um movimento duplo dos auges dos planetas (que definem a localização zodiacal das suas excentricidades): por um lado um movimento regular de precessão (com nas tabelas de Ptolomeu ou al-Battani), por outro um movimento de accessus et recessus (como nas tabelas de Toledo). A solução englobava doravante ambos os expedientes. E optou-se por registar os movimentos médios planetários na Nona esfera, numa abordagem estritamente tropical (respaldada nos equinócios e solstícios) pois esta é a esfera verdadeiramente "fixa" num sistema geocêntrico. [As tabelas de Toledo e as de al-Khwarizmi baseavam-se em posições siderais (medidas a partir das estrelas concretas) e, consequentemente, na Oitava esfera.] Mais tarde, no modelo de Peuerbach, que também procurou saber como oscilavam os pólos e os solstícios no conjunto da "mecânica" da esfera, estes últimos descreviam necessariamente uma espécie de lemniscata (curva em forma de "8").

Em resumo, "precessão" é o termo utilizado para descrever um ritmo constante no incremento das posições tropicais (referidas aos anguli, mormente ao ponto Aries) das estrelas fixas; "trepidação" refere-se a modelos de acordo com os quais a precessão é variável (podendo até assumir valores negativos para determinados intervalos de tempo, v. José Chabás e Bernard R. Goldstein, The Alfonsine Tables of Toledo, Springer, 2003, p.256). Note-se que o termo "trepidação" não surge nos textos medievais: encontramos "accesus et recessus" [Ár. al-iqbāl wa l-idbā] (Op, cit., p.217). O verdadeiro objectivo era determinar uma "precessão total" combinada. Nas tabelas siderais, considerava-se o movimento da Oitava esfera; nas tropicais (como as Alfonsinas), o da Nona, pois "framework" baseava-se nos equinócios e solstícios (longitudes medidas do ponto Aries).

Para uma abordagem da teoria tal como emergiu em textos indianos, v. David Pingree, “Precession and trepidation in Indian astronomy before A.D. 1200”. JHA 3, 1972, pp.27–35.

Ptolomeu não considerou qualquer expediente deste tipo e, no Almagesto, apenas se refere a componente linear precessional (1º=100 anos). Contudo, uma passagem do "Pequeno Comentário" às chamadas Tabelas manuais (Procheiroi kanones) do alexandrino, escrito por Θέων (Teão) de Alexandria (séc. IV), refere (cap. 12) que algumas opiniões de antigos astrónomos/astrólogos [οἱ παλαιοὶ τῶν ἀποτελεσματικῶν] faziam intervir um demorado deslocamento nas posições dos pontos solsticiais em 8º para leste e depois de volta novamente (Anne Tihon, Le “Petit commentaire” de Théon d’Alexandrie aux Tables faciles de Ptolémée: histoire du texte, édition critique, traduction, Studi e testi 282. Città del Vaticano: Biblioteca Apostolica Vaticana, 1978, pp.236–237). É muitas vezes considerada uma primeira referência à célebre "trepidação" medieval. Mas tudo o que se pode afirmar é que é legítimo interpretar a fórmula de Teão como sendo uma conversão da estrutura de referência tropical de Ptolomeu numa estrutura de referência sideral, cogitação fortemente suportada pela predominância de longitudes siderais na astronomia dos papiros e nos textos astrológicos antigos, pelo menos até ao séc. III (Alexander Jones, "Ancient Rejection and Adoption of Ptolemy’s Frame of Reference for Longitudes", in: Jones, A. (ed.), Ptolemy in Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century, Springer, 2010, pp. 15-17). A única referência antiga alternativa parece surgir no séc. V em Proclus (Hypotyposis 3.54; v. Carolus Manitius (ed.), Procli Diadochi hypotyposis astronomicarum positionum, 1909, pp.66–68) e num scholion (glosa, comentário) do mesmo trabalho (nº 316 em Manitius, 1909, p.275).

A persistente ligação da teoria (que assumiu vários modelos geométricos) a Thābit ibn Qurra (também grafado "ben Korra"; "ben Chorath" em Delambre), o tradicional responsável por todo este "equívoco", foi liminarmente rejeitada por F. Jamil Ragep (Naṣīr al-Dīn al-Ṭūsī’s memoire on astronomy (al-Tadhkira fī ʿilm al-hayʾa), 2 vols., 1993, pp.400-408) com argumentos aceites por N. Swerdlow e O. Neugebauer (1984, I, p.43). Como Elly Dekker salienta, no século X alguns modelos de trepidação foram expendidos no Kitāb Ḥarakāt al-Shams por Ibrāhīm ibn Sinān (908–46), que curiosamente era neto do mencionado Thābit. (Illustrating the Phaenomena: Celestial Cartography in Antiquity and the Middle Ages, Oxford University Press, 2013, p.281). Esta teoria foi particularmente bem recebida no al-Andalus. Todavia, como Julio Samsó e Mercè Comes demonstraram, havia pouca uniformidade nas opiniões, proliferando diferentes modelos. Até ao séc. XV, o método mais utilizado, pela sua visibilidade, foi o incluído nas Tabelas Alfonsinas.

O movimento de trepidação seria, em princípio, próprio da Oitava esfera. Com origem na revitalização Islâmica do séc. IX, a teoria (re)nasce na sequência da tentativa de determinação do valor exacto do lento movimento de Precessão. Este somente podia ser compreendido na comparação com valores documentados numa época distanciada. Recorreu-se assim às informações de Ptolomeu (que por seu lado se baseavam na comparação com as observações de Hiparco). Os astrónomos islâmicos calcularam assim o valor de 1º=65 anos em relação aos dados de Ptolomeu (A.D. 139). Foram ludibriados pela estimativa exagerada do astrónomo alexandrino (1º=100 anos), pois se tivessem comparado directamente com o valor da época de Hiparco teriam chegado a um resultado muito próximo do real. Assim não aconteceu e gerou-se o equívoco de que a Precessão estaria a acelerar. Apesar da cautela de astrónomos como Al-Battani perante esta difícil questão escassamente provida de dados observacionais fiáveis, surge esta equívocada resposta atribuída (de modo provavelmente espúrio, como vimos) a Thābit, a partir de um tratado que subsiste apenas na sua tradução latina: De motu octave spere (v. Thomas Hockey et al. (eds.). The Biographical Encyclopedia of Astronomers, Springer Reference. 2007, pp. 1129-1130). Estava "destinado" que a Astronomia, através dos seus melhores praticantes, mergulhasse por séculos nestas investigações que radicavam em imprecisões observacionais e erros, todavia dificilmente evitáveis nesses tempos. Como J. L. E. Dreyer explicou, imaginou-se uma curiosa articulação com uma eclíptica "fixa" da nona esfera. A "fixa" intersectava o equador em dois pontos segundo um ângulo de 23º 33'; a eclíptica "móvel" (que é a observável, na oitava esfera) estava ligada a dois pequenos círculos diametralmente opostos (amiudadamente representados em antigos esquemas do modelo geocêntrico), os centros das quais coincidiam com os equinócios médios e cujos raios mediam 4º 18' 43". Os pontos tropicais móveis de Cancer e Capricornus nunca abandonavam a eclípica "fixa" mas avançavam e recuavam a extensão de 8º 37' 26"; os dois pontos que se situam a 90º destes percorriam os pequenos círculos mencionados. Assim, a eclíptica móvel alternadamente elevava-se e descia relativamente à posição da eclíptica "fixa", enquanto os pontos de intersecção do equador e da "móvel" (pontos equinociais) avançavam e recediam 10º 45', em ambas as direcções. (A History of Astronomy..., 1953 (1905), p.276). Apesar de ibn Qurra (ou do pseudo-ibn Qurra) não o referir, a variação da obliquidade da eclíptica seria necessariamente afectada. O lugar da maior declinação do Sol altera-se continuamente, pois situa-se sempre a 90º das instersecções do equador com a eclíptica fixa. A maior decinação tanto acontece em Gemini como em Cancer (Delambre, M., Histoire de L'Astronomy du Moyen Age, Paris, M.me V.e Courcier, 1819, p.74). Interpretando toda esta teoria como uma enorme e desnecessária confusão, Delambre humorizou (p.73):

"Tout ce qu’on sait et ce qu'on peut dire de cet arabe [referindo-se ao autor associado à teoria], c’est qu’il a été le Ronsard de l’Astronomie.":
Réglant tout, brouilla tout, fit un art à sa mode;
Et toutefois long-temps eut un heureux destin.

Foi uma teoria muito fluida e repleta de variantes. Combinava-se frequentemente a precessão de 1º em 100 anos (valor de Ptolomeu) com a "oscilação". Segundo J. L. E. Dreyer, na época de Alfonso X, percebeu-se que os equinócios haviam recedido muito para além do que a teoria permitia. Doravante, acreditava-se que os equinócios percorriam todo o círculo em 49000 anos, sendo o período de inequalidade da trepidação de 7000 anos, "so that in a sort of Great Jubilee year everything was again as it had been in the beginning." (Op. cit., p.278).

[Resume-se seguidamente, com um esquema, o essencial da excelente explicação passo a passo de James Evans, The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p. 274 et seq.]

Com a ajuda do esquema anterior (J. Evans: 1998, p.277), verificamos que neste sistema o Equador Celeste (AJ) é intersectado em A pela Eclíptica Fixa ("Fixed Ecliptic", que não é a real, observável, mas uma referência fictícia inscrita na 9ª Esfera). Esta referência é "fixa" em relação ao Equador, com o qual faz um ângulo de 23º 33', de acordo com a estimativa da época. O pólo do Equador é o ponto P. O coluro solsticial (PIJ), que não é o real, observável, intersecta a Eclíptica Fixa e o Equador perpendicularmente. Ademais, com centro em A (e no ponto diametralmente oposto, não mostrado no esquema) há pequenos círculos cujo raio é de cerca de 4º (4º18'). Tudo isto são estruturas de referência fixas, coerentes entre si, situadas na 9ª Esfera [v. estes pequenos círculos no penúltimo anel do esquema do Cosmographicum liber de Apianus reproduzido mais acima nesta página].

Percorrendo este pequeno círculo com centro em A está o ponto C (o princípio de Aries), movendo-se uniformemente, pelo que a amplitude do ângulo assinalado pela letra Betaaumenta gradualmente também de modo uniforme (segundo o pseudo-Thabit, percorria os 360º em 4182 anos do Calendário Islâmico, 4057 no Calendário Juliano). Do outro lado acontece algo semelhante com o princípio de Libra. Mas estes dois pontos (Aries e Libra) estão sempre opostos em relação ao Equador, quando um está a Norte o outro está a Sul e vice-versa (como o sistema mecânico das rodas de uma antiga locomotiva a vapor).

A Eclíptica real, verdadeira ou observável (chamada Móvel, "Moveable" no esquema) movimenta-se em relação ao Equador. Passa pelo ponto C (princípio de Aries) e pelo ponto oposto que assinala o início de Libra (não mostrado no esquema). O verdadeiro Ponto Aries Equinocial, observável, é a intersecção desta Eclíptica Móvel com o Equador.

O ponto D (início de Cancer) fica sempre a 90º de C e permanece sempre na Eclíptica Fixa (que sabemos ser nocional), tendo aí um movimento de avanço e recuo. Também é fictício! O verdadeiro ponto solstícial observável em Cancer está representado no esquema pelo símbolo que tradicionalmente identifica este signo e fica, naturalmente, na Eclíptica Móvel (a observável).

- Ver segundo esquema (Evans, ibid.) com exposição diacrónica do funcionamento (nomeadamente o accessus et recessus da estrela "S") preconizado por esta "criativa" teoria.

Nesta teoria, o primeiro ponto de Aries mudaria de posição, por vezes na sequência dos signos, outras vezes contra esta sequência, com um desvio máximo de 9 graus. Para terminar, convém referir que todas as estrelas e também os "auges " (apogeus) dos planetas estão plasmados na esfera da Eclíptica Móvel e sujeitos à sua movimentação.

A linha que une o apogeu e o seu oposto (perigeu) é a chamada linha dos ápsides. Era, no passado medievo chamada linha do aux (pl. auges), a palavra 'aux' vem do Árabe 'awj' ("apogeu"). Em Latim habitualmente sofre a inflexão (gen. augis, pl. auges)]

Todos os modelos foram finalmente rejeitados pelo exemplo e prestígio de Tycho Brahe (que descartou semelhante procedimento) em finais do séc. XVI, sendo uma Precessão constante fixada bem perto do valor actualmente aceite de 1º em 72 anos. A fórmula actual é: p = 50".2564 + 0".000222 t, onde "t" é o nº de anos desde o referencial 1900 (avançando ou recuando nos séculos, + ou -).

Os principais contributos da Idade Média para a Astronomia foram o desenvolvimento dos relógios mecânicos e a adopção do sistema numérico conhecido como indo-arábico (notação decimal inventada na Índia, talvez em torno de 500 A.D., na qual a posição do número mostrava que potência de 10 representava, enquanto para as posições vazias se utilizava o zero).

Os relógios mecânicos são a mais importante contribuição tecnológica medieval. Os primeiros "horológios" (como se dizia entre nós) funcionais surgem no século XIII. Não eram ainda servidos por molas mas sim por sistemas de pesos que desciam suspensos em cordas, e não eram rigorosos (David Bergamini, The Universe, "LIFE Nature Library", Time Inc., 1962, p.14). Basta referir que eram comummente acertados com a ajuda de relógios de Sol. Shakespeare humorizou com a sua imprecisão na comédia Love’s Labour’s Lost, quando Lord Berowne (ou Biron) diz (cena I, 3º acto):

"What, I! I love! I sue! I seek a wife!
A woman, that is like a German clock,
Still a-repairing, ever out of frame,
And never going aright, being a watch,
But being watch'd that it may still go right!"

Tornar-se-ão, todavia, gradualmente mais sofisticados. No século seguinte, alguns complexos relógios astronómicos mecânicos vão conseguir "capturar", emular e traduzir o grande fenómeno do Universo, abrindo o caminho para os magníficos e refinados mecanismos que vão ser construídos ao longo dos séculos seguintes. Como exemplos de vanguarda, ainda no século XIV, o instrumento concebido por Richard de Wallingford, descrito no Tractatus Horologii Astronomici, de 1327 [vide monografia de referência de J. D. North, implementada a partir do estudo do MS Ashmole 1796: "God’s Clockmaker: Richard of Wallingford and the Invention of Time" (London: Hambledon, 2005)] ou o Astrarium de Giovanni de' Dondi (1318-1389).

O Astrarium, terminado em 1362, demorou dezasseis anos a construír. O seu complexo mecanismo de rodas dentadas traduzia os movimentos astronómicos, nomeadamente os planetários. Nesta reconstituição (Smithsonian Institution), os mostradores que vemos em cima representam, respectivamente, os movimentos de Marte, Sol e Vénus; o mostrador central mais abaixo é um relógio de 24 horas.

Com a prensa de tipos móveis de Gutenberg (c. 1440), a disseminação da informação incrementa a discussão de novas ideias:

The literature of the Middle Ages was handwritten. Writing a book could take months or years and it was done quietly, mostly in secluded monasteries, and also at universities, but here for academic circles only. The authors of the Middle Age were not seeking to reach the public. Literature served the purposes of remembering and preserving, of edifying (in the case of religious literature), and of transmitting knowledge (in the case of scientific literature). But in Early Modern Times Societies in many European countries, especially in Italy and in Germany, were in a state of ferment political, artistic, and religious. Literature was now intended to dominate through new ideas, personal opinions of the authors, was intended to influence society and bring about change. This desire to argue and agitate could only be realized by mass media. And that was now made possible by the so-called “pamphlets”, a result of the new printing technology. (Gustav-Adolf Schoener, The Flood of 1524: The First Mass-media Event in European History, in: Esoterica, vol. IX, Michigan State University, East Lansing, Michigan, 2007, p.168)

Como J. Pacheco resumiu, conjuga-se a universalidade consubstanciada na invenção da tipografia (depois da mais limitada xilogravura, gravação em madeira) com o uso do Latim como língua internacional, concluíndo que: "a inovação de Gutemberg vai alterar a estrutura das relações culturais, políticas e económicas na Europa." (A Divina Arte Negra e o Livro Português: Séculos XV e XVI, Vega, s/d (1988), p.35).

No século XV, muitos textos clássicos voltaram a estar disponíveis nos originais e muita produção contemporânea ganha visibilidade. Incidentalmente, a estética renascentista procurava debalde nos modelos ptolomaicos a "harmonia" que o redescoberto Platão afirmava ser apanágio do Kósmos. Filosoficamente, as qualidades literárias dos seus diálogos e o seu elegante desenho matemático começavam a suplantar o naturalismo aristotélico.

Seguindo de perto a síntese de Noel Swerdlow (Astronomy in the Renaissance, in: Astronomy Before the Telescope, Op. cit., 187 et seq.), as peripécias que conduzem a uma "nova astronomia" começam a esboçar-se com a recuperação e exposição, por Johannes Müller de Königsberg (latiniz. Regiomontanus, João de Monte Régio, 1436-1476), dos métodos matemáticos e observacionais de Ptolomeu (bem como de alguns acréscimos feitos por autores Islâmicos), ainda no quadro da física da revolução das esferas como causa dos movimentos celestes. Esse génio do cálculo procurou incrementar a precisão, denunciando as anomalias e disparidades observáveis nos fenómenos, mormente os desfasamentos entre o calculado e o efectivamente observado. O próprio nunca imaginaria a enorme mudança que precisaria acontecer. Os erros por si apontados revelaram-se tão sérios que as soluções vão precisar de Tycho, Kepler, do perspicillum (telescópio) de Galileu e da total reformulação da Astronomia nos finais do séc. XVI e início do seguinte.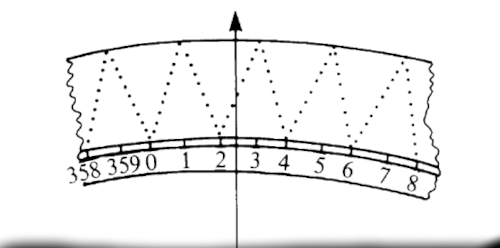

Brahe usou o sistema de pontos transversais (em ziguezague) nas graduações dos instrumentos introduzido por Johann Hommel (Homilius) ou por um tal Scultetus, mas B. R. Goldstein afirma que esta escala oblíqua recua a Levi ben Gerson, o inventor do chamado "Báculo de Jacob". Permitia leituras com maior precisão. Na ilustração, valor seria 2.4 (Thurston, Op. cit., fig. 10.7). Ver ilustração numa edição de 1598 da Astronomiae Instauratae Mechanica de Tycho Brahe.

O Nónio
Pedro Nunes apresentou este sistema no De Crepusculis (1542). Uma ideia engenhosa (v. ilustração do seu principio; E. Fourrey, Curiosités Géométriques, Paris, 1907), que podia ser acoplada a qualquer astrolábio ou quadrante. Num quarto de um "círculo completo", de raios arbitrários e diferentes, desenhavam-se 44 arcos de 90° cada, dividindo o maior em 90 partes, os seguinte em 89, 88, 87 e assim por diante. O último em 46. E colocavam-se os números em todas essas divisões. Como Dreyer explicou na sua biografia de Tycho Brahe (A Picture of Scientific Life and Work in the Sixteenth Century, Dover, 1963 [1890], p.329), os círculos eram divididos de modo que a alidade em qualquer posição (de visada) tocava (com maior ou menor precisão) uma marca de divisão num dos 45 círculos. A indicação dessa marca seria multiplicada por 90/n, onde n era o número de divisões no arco em que a marca tocada pela alidade se encontrava. Infelizmente, não era nada prático, pois não é fácil dividir um arco em 87 ou 71 partes iguais, e o observador geralmente ficaria em dúvida sobre qual divisão estava mais próxima da alidade. A utilização era onerosa e amiudadamente pouco precisa pois, segundo G. Bigourdain, aconteciam erros até 10' ou 12' (L'Astronomie: Evolution des idées et des Méthodes, Paris, E. Flammarion, 1920 [1911], p.120). Jean-Baptiste Delambre (Histoire de la Astronomie au Moyen Âge, pp.402 et seq.) explicou a complexidade da utilização e a necessidade de uma construção rigorosíssima. Investigou meticulosamente e apresentou de forma tabelada os erros que o método devolvia, consoante a escolha da subdivisão num dos 44 arcos e da fracção em causa (e.g., décimas, quartos). Conclui: "L'auteur n'a jamais eu la prétention de faire trouver l'angle à la seconde: mais pour l'avoir en minutes, il faudrait que l'angle exprimé en minutes fût exactement divisible par l'un des quarante-quatre diviseurs" (p.405). Tycho Brahe chegou a adaptar o sistema a três dos seus instrumentos mas abandonou-o de seguida, optando pelas chamadas "transversais". E assim o nónio foi descartado. A (diferente) solução inventada por Pierre Vernier em 1631 (com algumas sugestões de Clavius publicadas na Opera Mathematica [Mogúncia, 1612]), mostrou-se mais simples, precisa e eficiente. Ainda é utilizada.

Regiomontanus escrevera um Epitome do Almagesto, que fora muito mais do que uma simples descrição resumida da metodologia do alexandrino, antes uma espécie de "recensão crítica". Depois elucida, optimiza e publica textos acerca das ferramentas essenciais. Primeiro vem a Trigonometria, alicerce de toda a computação, no seu De triangulis omnimodis ("Dos triângulos de todos os tipos"). Também calculou enormes tabelas de senos para cada minuto de arco. A disponibilização destas tabelas rigorosas será muito importante. Cálculos precisos não são possíveis sem tabelas trigonométricas precisas. E, com a precisão, as anomalias tornam-se mais óbvias. Depois vem a Astronomia Esférica, geometria e trigonometria dos círculos da Esfera Celeste, essenciais para a determinação das horas dos nascimentos, culminações e ocasos, conversão de coordenadas, resolução de componentes de paralaxe, etc. Enfim, não menos importante, para todas as aplicações astrológicas (limites das casas, direcções dos significadores, projecções, etc.). Assim sendo, calculou as Tabulae directionum. Ainda as Tabulae primi mobilis com soluções para triângulos esféricos rectângulo com intervalos de 1 grau, bem como problemas demonstrativos da sua utilização. Seguem-se mais ferramentas, como o seu Kalendarium ou as ambiciosas Ephemerides para 32 anos, com as posições diárias dos luminares e dos planetas, bem como os aspectos astrológicos (Colombo, na sua viajem histórica, fez-se acompanhar pelas Ephemerides, bem como pelo Almanach Perpetuum de Zacuto.). Entretanto, Bernhard Walther (1430-1504) foi um dos primeiros a fazer observações sistemáticas e precisas, continuadas pelo seu colaborador Johannes Schoner que as publicou e que serão depois usadas por astrónomos como Tycho.

Os métodos antigos serão ainda, como veremos, fielmente aplicados pelo célebre Copernicus, que os estendeu à teoria heliocêntrica. Para ele (ao contrário da opinião comum), nunca esteve em causa a negação da dualidade aristotélica das "naturezas": a etérea do movimento circular e a sublunar corruptível, do movimento rectilíneo. Nesse particular, uma mudança mais radical virá com Tyge (latiniz. Tycho) Brahe (1546-1601), cuja instrumentação melhorada e vasto acervo de observações [ou considerationes, palavra que possuía na época esse significado técnico] de precisão inaudita optimizarão os métodos existentes, enquanto a sua argumentação provará a inexistência das esferas sólidas, nas quais a Astronomia se respaldava desde a Antiguidade. Assim, no De Mundi Aetherei recentioribus phaenomenis (1588) rejeitava-as e mantinha-as apenas enquanto expediente útil: "...e as [esferas ou "orbes"] que foram concebidas pelos autores ["Artifices"] para salvar as aparências ["pro saluandis Apparentiis"] existem apenas na imaginação, para que a mente conceba os movimentos que os sidéreos cumprem no seu curso e, por intermédio da geometria, determinar numericamente os seus movimentos pelo uso da aritmética. (...) Claro, quase toda a antiguidade e também muitos filósofos modernos acham certa e têm por certa a ideia de que os céus sejam formados de uma substância dura e impenetrável, que esta seja separada em várias esferas, e que os corpos, fixados em algumas destas esferas, assim revolvam ["circumgyrantur"]. Mas esta opinião não corresponde à verdade..." (Tychonis Brahe opera omnia, ed. J.L.E. Dreyer, Tomus IV [1922], 222.24-35 [trad. nossa]):

"He [Tycho] observed and measured and did both more patiently and more accurately than any man before him. As regards specific points, he proved that a bright comet was several times as far away from the earth as the moon is, hence that comets were astronomical and not meteorological phenomena. He proved that the star of 1572 was a fixed star, hence that changes go on in the far-away “sphere” of the fixed stars. He determined the precession of the equinoxes to be 51 seconds of arc per year and showed it to be continuous; in short, he killed the “trepidation of the equinoxes.” He produced perfect positions for 777 stars, but he did not finish his catalogue." (Willy Ley, Watchers of the Sky: An Informal History of Astronomy From Babylon to the Space Age, Viking Press, 1964 (1963), p.92).

A necessidade de encontrar um novo enquadramento físico e o resultado das observações sistemáticas de Tycho (precedidas pelas efectuadas por Bernhard Walther e pelo observatório instalado pelo Landgrave Guilherme [Wilhelm] IV de Hesse (1532-1592) em Kassel) levarão mais tarde Kepler a ir muito além de todos ao descobrir novos princípios para a descrição precisa dos movimentos dos corpos celestes, baseados em premissas completamente diferentes.

De Revolutionibus... (Norimbergae, Apud Ion. Petreium, Anno 1543; exemplar da 1ª edição do acervo da Biblioteca da Ajuda (BA 35-XI-5)

Nicolaus Copernicus (Mikołaj Kopernik em Polaco; Niklas Koppernigk em Alemão, 1473-1543) propôs, como sabemos, um modelo heliocêntrico (ou melhor helioestático, já veremos porquê) que baniu a Terra do centro do Universo, todavia continuando a acreditar firmemente na circularidade dos movimentos e nas esferas "sólidas" do passado, deste modo recorrendo obrigatoriamente a epiciclos. A teoria não resultou de novas observações, foi antes o resultado intelectual de uma demanda por uma mais bela e harmoniosa (no sentido pitagórico e platónico) estruturação do sistema planetário. A extensa pesquisa de Owen Gingerich demonstrou que para a maioria dos astrónomos da época, o maior conseguimento da teoria de Copérnico foi a eliminação do punctum aequans, satisfazendo o antigo princípio estético de que os movimentos celestiais deveriam ser uniformes e circulares, ou explicados por componentes uniformes e circulares (The Book Nobody Read..., Walker & Company, 2004). O Ad lectorem (não autorizado) adicionado por Andreas Osiander (que acompanhou a impressão do De Revolutionibus...), declara que "o dever do astrónomo é registar, através de competentes e diligentes observações, os movimentos celestes, tendo depois que propor as suas causas, ou melhor, hipóteses, pois não se pode almejar conhecer as verdadeiras razões..." [trad. nossa]. Assim defendia a teoria enquanto modelo matemático, amenizando a profunda implicação filosófica que de facto representava. A intenção de Copernicus, que o próprio enfatizou, era preservar o movimento circular uniforme adulterado nos modelos ptolomaicos. Nesse desiderato técnico foi, segundo algumas opiniões, provavelmente influenciado (por vias sinuosas e ainda desconhecidas) pela chamada "Escola de Maragha", estabelecida na Pérsia do séc. XIII (vide Swerdlow, N., Copernicus and Astrology, with an Appendix of Translations of Primary Sources, Perspectives on Science, vol. 20, no. 3, MIT, 2012, p.372). Mas esta argumentação não nos parece suficientemente convincente.

Todavia, o cenário coperniciano parece, apesar das consequências, ser pouco inovador ou eficiente. Convém relembrar que Copernicus não colocou o Sol no centro mas perto do centro e que, no seu sistema, a Terra não se movimenta como os restantes planetas (é o único que não tem epiciclo). Otto Neugebauer (On the Planetary Theory of Copernicus, 1968; .PDF, 665KB), sempre acutilante e competente, desconfia da interpretação contemporânea prevalecente: "the ever increasing modern tendency toward hero worship on the basis of "ideas" and disrespect for technicalities". Para ele, "...the Copernican theory is only a formal transformation of the Ptolemaic theory." (p.103), pois todos os procedimentos adoptados têm a sua réplica no Almagesto. Acrescenta que o objectivo não foi abolir o aequans mas, tal como os antecessores Islâmicos (e.g., Ibn al-Shatir, al-Tusi), demonstrar que um epiciclo secundário seria capaz de produzir o mesmo efeito da utilização do famigerado punctum. [Ibn al-Shatir (Damasco, c.1350) conseguiu eliminar não apenas o aequans mas outros círculos que levantavam objecções, abrindo caminho para um sistema mecanicamente mais aceitável. Num quadro geocêntrico, antecipou soluções matemáticas - todavia não conceptuais - de Copérnico. Mas parece ter sido desconhecido na Europa.] E o modelo tornou-se, na realidade, ainda mais complicado do que o que pretendia substituir. Neugebauer salienta (como alguns antigos matemáticos de vanguarda como Vieta [François Viète, 1540-1603] já haviam feito) que os procedimentos adoptados são arcaizantes, sempre procurando emular Ptolomeu. Como em todos os modelos "circulares", a determinação dos parâmetros planetários exigia 3 posições médias e 3 verdadeiras, necessárias para caracterizar o círculo ou órbita. Foi assim desde Apolónio até Kepler. Osiander (no já mencionado prefácio) acaba por ter razão ao considerar estarmos somente perante um modelo cinemáticoe não uma explicação dos fenómenos. Ainda segundo Neugebauer, a matemática de Copernicus não é brilhante, há muitos erros, metodologias incoerentes e utilização de informação datada e imprecisa. Vale a pena seguir a detalhada exegese técnica (todavia demasiado complexa para o típico historiador contemporâneo). Como maior contribuição de Copernicus, o grande historiador da Brown University assinalou a abertura do caminho para a determinação das dimensões absolutas do sistema planetário. Em síntese, sem Tycho Brahe e Kepler, nada de matematicamente relevante se teria extraído da teoria:

Modern historians, making ample use of the advantage of hindsight, stress the revolutionary significance of the heliocentric system and the simplifications it had introduced. In fact, the actual computation of planetary positions follows exactly the ancient pattern and the results are the same. The Copernican solar theory is definitely a step in the wrong direction for the actual computation as well as for the underlying cinematic concepts. The cinematically elegant idea of secondary epicycles for the lunar theory and as substitute for the equant - as we now know, methods familiar to a school of Islamic astronomers - does not contribute to make the planetary phenomena easier to visualize. Had it not been for Tycho Brahe and Kepler, the Copernican system would have contributed to the perpetuation of the Ptolemaic system in a slightly more complicated form but more pleasing to philosophical minds. (p.103)

Copernicus inseriu a seguinte nota de Plutarco (em grego no original) na carta ao Papa Paulo III (prefácio do De Rev.):

"Outros pensam que a Terra está fixa. Mas o pitagórico Filolau diz que ela gira em órbita à volta do fogo [tratava-se de um "Fogo central", não do Sol], num círculo oblíquo à semelhança do Sol e da Lua. Heraclides do Ponto e o pitagórico Ecfanto atribuem movimento à Terra, não de maneira a sair da sua posição mas girando como uma roda do Ocidente para Oriente, à volta do seu centro" (As Revoluções dos Orbes Celestes, A. Dias Gomes e Gabriel Domingues (trad.), Fundação Calouste Gulbenkian, 3ª Edição, 2014).

Ecfanto, bem como o discreto Hicetas (que talvez seja o Nicetus Syracusanus também referido no livro de Copernicus), podem ter sido somente personagens dos diálogos de Heraclides. Mas há referências que parecem recuar a Theophrastus, ainda contemporâneo de Heraclides (v. Pythagoreanism, in: Stanford Encyclopedia of Philosophy), tratados como históricos na posterior doxografia. Heraclides do Ponto (Ponticus), c.390-c.310 a.C., colocou a hipótese da rotação diária da Terra sobre o seu eixo e, em muitas resenhas históricas, surge amiudadamente referido como proponente de soluções heliocêntricas. Segundo Bruce Eastwood (Heraclides and Heliocentrism: Texts, Diagrams, and Interpretations, 1992), não existe qualquer fonte documental que o corrobore: "Nowhere in the ancient literature mentioning Heraclides of Pontus is there a clear reference for his support for any kind of heliocentrical planetary position" (p.256). Ou seja, estamos perante mais um exemplo de repetição acrítica.

O movimento axial era anteriormente visto como implausível (habitava-se "terra firma") e supostamente contrariado pelo movimento dos projécteis, como as setas. Não prioritariamente por argumentos astronómicos. Celio Calcagnini, que conheceu Copernicus em Ferrara, sugere (de modo todavia vago) a rotação da Terra: "Quod Caelum Stet, Terra Moveatur". Na Índia, por exemplo, Brahmagupta (no tratado Brāhmasphuṭasiddhānta, 628 A.D.) declara que Aryabhatta defendia que a Terra executava um movimento de rotação axial, opinião que refuta. Segundo Giorgio Abetti, Schiaparelli acreditava que esta ideia era proveniente de fontes gregas (History of Astronomy (trad, de Betty Burr Abetti), Abelard-Schuman, 1952, p.25). Como se sabe, a demonstração definitiva da rotação da Terra acontecerá somente em 1851, através da célebre experiência do Pêndulo de Foucault (Jean-Bernard Léon Foucault, 1819-1868), cuja alteração gradual no alinhamento determina que o planeta se desloca sob o plano de oscilação livre desse pêndulo. A experiência aconteceu no Panteão de Paris e utilizou um pêndulo com 67 metros de altura e, como peso, uma esfera de 28 kg.

Copernicus manteve-se sempre "próximo" de Ptolomeu e da tradição geral: "A renovação da teoria cósmica consistia numa transcrição do sistema ptolomaico, copiando os dados e observações e atribuíndo-lhes outros nomes: aquilo a que se chamava deferente de Marte' era agora chamada a sua 'órbita real'". (Pannekoek, Op. cit., p.193; trad. nossa). Manifesta excessiva reverência pelos autores pretéritos e, por isso mesmo, torna-se propenso a aduzir complicações como a trepidatio (precessão alternadamente lenta e rápida, um enorme equívoco da astronomia medieval), a que vai procurar responder complicando ainda mais o que já o era sem essa inexistência. A "renovação" e "simplicidade" do sistema eram fictícias. O seu livro revela um astrónomo tradicional, com ideias que acreditava já terem sido propostas, nada ousado. Mesmo tendo retirado a Terra da sua posição central, sentiu-se compelido a dar-lhe um paradoxal papel fundamental no seu novo sistema: para este "funcionar" sem o punctum aequans, e em resposta ao problema do diferencial das distâncias dos planetas no afélio e no periélio (posições 1 e 3 no esquema seguinte, respectivamente a posição mais afastada e a mais próxima do Sol), não é o luminar que está, na realidade, no centro do sistema. Os planetas são ainda obrigados a percorrer um pequeno epiciclo cujo raio está relacionado com a distância do Sol ao ponto S. O centro é, entretanto, ocupado por esse ponto (S, no esquema seguinte), que é, pasme-se, o centro da órbita da Terra. Este estranho "Centro do Mundo" é, consequentemente, o centro das órbitas dos restantes planetas. Demais, o ano terrestre (o período de revolução da Terra) estava, no sistema, intimamente ligado com os movimentos dos dois planetas doravante inferiores (Mercúrio e Vénus). Ou seja, Copernicus, não tirando todas as conclusões da sua escolha "heliocêntrica", continuará a fazer passar todos os planos orbitais pela Terra, e consequentemente as linhas dos nodos (o que perpetuou as consideráveis dificuldades na comparação com as observações, por exemplo, das latitudes dos planetas interiores).

Em resumo, os planetas orbitam o centro da órbita da Terra e não o Sol. Esta circunstância arrevesada compromete o que Copernicus afirma, no início do De Revolutionibus, quando argumenta que o lugar de tão proeminente astro (o Sol, a que chama lucerna mundi) deveria ser o centro do Universo. O sistema não é, efectivamente, heliocêntrico, apenas heliostático. (vide e.g., Pannekoek, Op. cit., p.193 et seq.).

O ponto S, e não o Sol, assinala o centro do Universo coperniciano; fonte: Pannekoek, A., A History of Astronomy, Op. cit., p.194

Copernicus fez uma síntese de um sistema heliocêntrico com o aparato geométrico da astronomia de Ptolomeu, do qual nunca se afastou. No seu Comentariolus (1514), concorda com "os Antigos", quando estes afirmavam como seria absurdo se os corpos celestes não se movessem uniformemente em círculos perfeitos. Segundo Zdenek Kopal, Copernicus foi o último desses grandes 'antigos' - um companheiro espiritual de Hiparco ou Ptolomeu (Widening Horizons, Man's Quest to Understand the Structure of the Universe, Taplinger Publishing Co., 1971, p.52). Kopal acrescenta que algumas das ideias inovadoras dos ulteriores auto-denominados "copernicianos" deixariam Copernicus horrorizado. Mas, apesar de conservador, foi o primeiro a tentar essa síntese. Aí reside a sua estatura na História da Astronomia.

Kepler terá afirmado que Copernicus "nem sabia quão rico era", e que "mais tentou interpretar Ptolomeu do que a Natureza". De facto, esteve longe de desenvolver aquilo a que hoje habitualmente chamamos "Sistema Coperniciano" (o seu sistema não era, de facto, exactamente aquilo que actualmente assim nomeamos) mas, em todo o caso, foi pretexto para uma alternativa que, após imensas convulsões, viria a alterar a nossa imagem do Universo (vide Dreyer, J. L. E., Op. cit., 342 et seq.). A. Pannekoek reconhece (Op. cit., p.193) que significou uma perturbação da mundividência vigente e que, com o disseminar da ideia, acabou por influenciar o pensamento moderno desde então. Como Massimo Cimino nos recordou, historiadores e filósofos salientaram a alteração de categoria filosófica alcançada pelo trabalho de Copernicus ao desviar o enfoque ptolomaico na tradução das aparências dos movimentos dos corpos celestes, para uma afirmação da realidade dos próprios movimentos. (The Importance of the "Precession" and the "Lunar" Theories in the Internal Structure of the Revolutionibus, in: Colloquia Copernicana III - Astronomy of Copernicus and Its Background, Toruń 1973 [publ. Ossolineum, 1975], p.137)

As novas tabelas Pruténicas (i.e. "prussianas", em honra do duque da Prússia, protector do seu autor, Erasmus Reinhold), Tabulae prutenicae em Latim, publicadas em 1551 (reimpr. em 1562, 1571 e 1585) basearam-se nos métodos do De revolutionibus.

O sistema de Copérnico (detalhe) na Harmonia Macrocosmica (lâmina 5), de A. Cellarius (1660)

O sistema foi defendido por Michael Maestlin (1550-1631), Thomas Hood (1556-1620) e Galileu Galilei (1564-1642), entre outros. Galileu será importante em diversas abordagens. Antes do italiano, um objecto em repouso era considerado como estando na sua situação normal na natureza. Surge então o conceito de 'Força' e de 'Movimento Uniforme'. Contra os argumentos dos detractores da rotação da Terra, o sábio constatou que as aves e a própria atmosfera partilhavam a rotação e assim a acompanhavam por inércia. No Saggiatore ("Ensaiador"), Galileu declara que o "Livro da Natureza" se escreve em linguagem matemática.

Entretanto, em 1587, Tycho Brahe apresentou uma interessante alternativa geo-heliocêntrica (v. ilustração infra) de "compromisso" entre os sistemas ptolomaico e coperniciano. A hipótese cosmológica de Tycho procurou concitar as vantagens da abordagem heliocêntrica, mantendo todavia a Terra fisicamente colocada no centro do Universo, apesar da desvantagem de a órbita de Marte ser obrigada a intersectar a do Sol. Como Brahe havia provado à saciedade, não havia qualquer impedimento físico pois a observação dos cometas e da nova de 1572 comprovavam que não existiam esferas sólidas que transportassem os planetas nas suas órbitas. Tycho conceptualizou um medium mais fluído do que as esferas. Galileu, adepto do heliocentrismo, ficará exasperado quando, ajudando a provar empiricamente a obsolescência do sistema ptolomaico (pois observou com o seu tubo óptico fenómenos que antes ninguém havia observado), não conseguirá todavia desacreditar o de Tycho (e seus derivados, como o de Nicolaus Reimers Baer, conhecido como "Ursus", ou o de G. Battista Riccioli). [O sistema de Ursus, que Tycho acusou de plágio, deixava as estrelas fixas imóveis e fazia a Terra rodar no seu eixo, ao contrário do do dinamarquês; outras diferenças: as estrelas fixas estariam a diferentes distâncias e a esfera do Sol estava encapsulada na de Marte, não a intersectando, como acontecia no modelo de Tycho. O Fundamentum astronomicum de Reimers foi publicado em Estrasburgo em 1588]. As fases de Vénus, por exemplo, impossíveis no antigo modelo ptolomaico, estavam doravante naturalmente explicadas pois ambos os planetas a que agora chamamos "interiores" giravam em torno do Sol. Nas regiões Católicas, muitos astrónomos, nomeadamente jesuítas, adoptaram confortavelmente o sistema de Tycho ou uma ou outra variante.

Brahe promoverá observações sistemáticas e precisas nos seus excelentes observatórios. Os seus antecessores contentavam-se em trabalhar com os dados das observações disponíveis, que chegavam do passado, fazendo observações somente quando inevitável e com instrumentos pouco precisos. Tycho alterou tudo isto. Construiu equipamentos de primeira qualidade, recorreu a metodologias rigorosas na observação, comparação e registo dos dados. Coligindo preciosa informação, desvelará as insuficiências do modelo prevalecente esbatendo a distinção entre as duas naturezas (sublunar e celestial), demonstrando que os cometas "atravessam" as supostas esferas (observou em particular o grande cometa de 1577) e determinando a ausência de paralaxe da "Nova Estrela" (Nova Stella) de 1572 em Cassiopeia, hoje chamada "Supernova de Tycho" (SN 1572). Este fenómeno extraordinário contradizia a imutabilidade aristotélica dos céus etéreos e incorruptíveis. Os fenómenos prodigiosos (cometas, etc.) eram até então explicados recorrendo a supostas "exalações" da atmosfera, coisas que aconteciam no contexto sub-lunar. Obviamente era um explicação errada. Todavia, excepto para os "resistentes" mais ardilosos, que recorreram a argumentos pseudo-teológicos de intervenções ad hoc da divindade (discussão de Fr. António Teixeira no seu Epitome das noticias astrologicas para a medicina, 1670, pp. 41-4; .PDF 498KB), nada podia escamotear as evidências: os céus também são palco de mudança e alterações. Não há duas naturezas distintas.

No que diz respeito ao papel da Igreja enquanto suposto "entrave" à teoria heliocêntrica, Thony Christie (na já citada review de um livro de David B. Teplow) esclareceu com propriedade:

"The Catholic Church only got sensitive about heliocentricity when in 1615, Galileo and Paolo Antonio Foscarini started telling it how to interpret the Bible, not a wise thing to do in the middle of the Reformation/Counter Reformation. Scholars were free to discuss or publish these models as long as they treated them hypothetically their actually scientific status at the time, and not as established fact. The suggestion of heliocentricity was never formally declared heretical, to claim otherwise is a myth. Galileo was not charged with heresy but with breaching a Church injunction not to hold or teach the theory of heliocentricity (as fact). He was found guilty of grave suspicion of heresy and not heresy, a completely different offense. Galileo in no way confirmed Copernicus’ result, he wasn’t able to. What results? Copernicus published a hypothesis, which was unsupported by the available empirical facts at the time."

Denuncia, adiante, o "modo hagiográfico" (the hagiography mode) e mitificador que assumem todos os comentários acerca de Galileu e da sua defesa do sistema de Copérnico:

"In the Dialogo [i.e. "Dialogo sopra i due massimi sistemi del mondo"] Galileo produces a lot of polemic and hot air but very few real arguments supporting the Copernican model, because he doesn’t really have any.". No referido Dialogo, Salviati (alter-ego do autor), argumenta em favor do sistema heliocêntrico.

Detalhe de ilustração do ms. Vossianus. Aratea (compêndio de conteúdos astronómicos, principalmente baseados do poema de Aratus) Carolíngia (séc. IX) que inclui textos e diagramas respaldados na astronomia de Martianus Capella e Plinius (o Velho) [clicar na imagem para aceder a versão mais ampla]. A Terra está no centro, com a Lua um pouco abaixo à sua direita; note-se que Mercúrio e Vénus orbitam o Sol (à esquerda). A ilustração apresenta, através das órbitas excêntricas, os ápsides (pontos mais próximo e mais afastado da órbita) dos planetas, segundo Plínio. No caso de Mercúrio e Vénus, desenham-se esses círculos bem como os círculos heliocêntricos. (Leiden Universiteitsbibliotheek, Special Collections, ms. Voss. lat. Q.79, f. 93v). Esta cosmovisão será mais tarde equivocamente associada ao nome de Aratus, sendo assim identificada, por exemplo, no célebre atlas Harmonia Macrocosmica de 1660 (lâmina 8: "PLANISPHÆRIVM ARATEVM Sive Compages ORBIVM MVNDANORVM EX HYPOTHESI ARATEA IN PLANO EXPRESSA")

É verdade. Galileu não conseguiu avançar qualquer evidência tangível. As fases de Vénus, podiam ser facilmente explicadas. Por exemplo, recuando ao velho sistema expendido por Martianus Capella através do argumento teorético avançado no lib. VIII do célebre De nuptiis: “...eorum circuli terras omnino non ambiunt, sed circa solem laxiore ambitu circulantur” ("os seus [de Mercúrio e Vénus] círculos, de modo algum envolvem a Terra, mas circulam em torno do Sol num caminho mais amplo"), amiudadamente referido em inúmeras glosas (que criaram variantes) e representado em muitos diagramas na época Carolíngia (muito antes dos textos fundamentais de Aristóteles ou Ptolomeu estarem disponíveis). Martianus não revela a origem do importante enunciado (vide Eastwood, Bruce S., Ordering the Heavens, Roman Astronomy and Cosmology in the Carolingian Renaissance, Leiden; Brill, 2007, pp.238-9; 288 et seq.). Riccioli, no séc. XVII, dizia que se tratava do "Sistema dos Egípcios" (esta atribuição foi relacionada com o comentário de Macrobius ao Somnium Scipionis). Mas também foi associando a Vitruvius, Beda, etc. Andreas Argolus, astrólogo e professor em Pádua publicou um tratado (Pandosion sphaericum, 1644) e adoptou esse sistema. A atribuição a Heráclides do Ponto (Ἡρακλείδης ὁ Ποντικός), particularmente seguida pelos académicos no séc. XIX (e.g., T. L. Heath, Pierre Duhem) carece de evidências. Plínio, quando discutiu Vénus e Mercúrio (Nat. hist., II, 72–73) havia descrito ambos os planetas (de modo algo estranho) como estando "debaixo do Sol", oscilando relativamente a este mas "nunca o cruzando".

Do ponto de vista dos Teólogos, a verdadeira questão não era o sistema propriamente dito mas o método para assegurar o conhecimento: a questão era se o "Livro da Natureza" poderia, de alguma maneira, rivalizar com as infalíveis Escrituras Sagradas enquanto caminho para a Verdade. (Owen Gingerich, The Great Copernicus Chase and other adventures in astronomical history, Sky Publishing Corp. and Cambridge University Press, 1992, p.113).

Surgem argumentos que expõem a absurdidade de um movimento diurno da gigantesca esfera celeste em torno de uma pequena Terra estacionária. Segundo as opiniões que Robert Burton [1577-1640] nos transmitiu no seu extenso "cosmos literário" (Anatomy of Melancholy...):

"What fury is that, saith Dr. Gilbert [autor do De magnete, v. infra], sufficient force, as Cabeus [Niccolò Cabeo] notes, that shall drive the Heavens about with such incomprehensible celerity in 24 hours, when as every point of the Firmament, and in the Equator, must needs move (so Clavius calculates) 176,660 in one 246th part of an hour: and an arrow out of a bow must go seven times about the earth whilst a man can say an Ave Maria, if it keep the same pace, or compass the earth 1,884 times in an hour, which is beyond human conceit : fleeter than a dart and a wind-swift arrow. A man could not ride so much ground, going 40 miles a day, in 2,904 years, as the Firmament goes in 24 hours ; or so much in 203 years, as the said Firmament in one minute ; which seems incredible." (The Anatomy of Melancholy [ed. F. Dell & P. Jordan-Smyth, 1930, p.423])

Contudo, o sistema de Copernicus levantava por sua vez novos problemas. Um destes era o da dimensão do Universo. Se a Terra orbitava em torno do Sol, a deslocação deveria, independentemente da estimativa do diâmetro da órbita, determinar um efeito de paralaxe nas estrelas observadas (devido às alterações da perspectiva nas diferentes posições da órbita, doravante por vezes muito afastadas entre si). Este efeito não era observado (como sabemos, as estrelas estão muitíssimo mais longe do que então era concebível). Tal como o sistema ptolomaico, o novo sistema também não explicava as desiguais velocidades observadas nas diversas fases do percurso de cada um dos planetas (pois nessa época ainda não se imaginavam as órbitas elípticas).

Johannes Kepler (1571-1630), com uma relação complexa com argumentos religiosos, astrológicos e com uma apetência matemática "neo-pitagórica", estudou as órbitas planetárias (baseado nos extensos dados observacionais de Tycho Brahe) e concluiu, a partir do esforçado estudo da órbita e Marte, leis que definitivamente as explicam, provando serem elípticas. Uma genial e absolutamente fundamental mudança de paradigma que ratificou o novo sistema heliocêntrico (mudança tão radical que Galileu nunca conseguiu acreditar nessas elipses, mantendo-se fiel à confusão dos desnecessários epiciclos; ler, por exemplo, a resposta que endossou a uma missiva de Federico Cesi em Junho de 1612). Segundo Z. Kopal: Most biographers of Kepler have been irritated by Galileo’s obtuseness in matters of cosmology, while the admirers of Galileo find it difficult to conceal their embarrassment. For although Astronomia Nova [o livro de Kepler] was on Galileo’s desk from 1609 (he received a ‘complimentary copy’ from Kepler), its contents seem to have been completely ignored by Galileo, for whom planetary orbits remained circles until the end of his life. (Widening Horizons..., Op. cit., p.82). Galileu não foi capaz de abandonar um "cripto-copernicianismo" nem conseguiu aduzir argumentos relevantes e definitivos em favor de algumas ideias correctas que expendeu, por exemplo aquelas relacionadas com os movimentos da Terra. Apesar da sua descoberta do isocronismo do movimento de um pêndulo (1589), a simples e famosa experiência do Pêndulo de Foucault (que provou a realidade da rotação do nosso planeta) ainda demoraria quase três séculos.

O movimento de Marte no céu acontece do modo seguinte: quando a Terra e o planeta se aproximam num mesmo sector das suas órbitas, em função da posição do Sol, Marte é observado da Terra num movimento cada vez mais lento até parecer parar no céu (contra o fundo de estrelas). Após este momento estacionário, recomeça o seu movimento na direcção oposta (retrogradação), mas retorna ao seu movimento "normal" algum tempo passado após a oposição. Esta "laçada" é aparente é somente um efeito de perspectiva: a Terra é mais rápida e apanha e ultrapassa o planeta mais afastado do Sol. Uma dificuldade consiste no facto de que o intervalo entre duas oposições é variável.

O astrónomo Christen Sørensen (dito Longomontanus) tentou enfrentar, a pedido de Tycho, as complexidades matemáticas do cálculo desta órbita. Mas Kepler era mais competente e persistente, tendo também a sorte de estarem reunidas duas condições: por um lado, a excentricidade relativamente forte da órbita de Marte (cujo comportamento praticamente irreconciliável com a antiga teoria determinou o enorme empenho no seu estudo), que colocou o matemático na trilha da utilização da oval e depois da elipse; por outro lado, a comparativamente fraca excentricidade da órbita terrestre. Como Z. Kopal resume, foi Kepler - não Copernicus - quem colocou o Sol no centro do Sistema Solar e descreveu as órbitas planetárias através de um modelo simples e exacto, com enorme alcance (Op. cit., p.66).

Como Arthur Berry explica, Kepler experimentou hipóteses e mais hipóteses, combinações de excêntricos, epiciclos e ponto equante. Até que chegou a um modelo que somente diferia 8' [minutos angulares] dos registos das observações. Mas o matemático sabia que os registos de Tycho eram precisos e, com a honestidade intelectual que o caracterizava, decidiu continuar a investigar, começou de novo e concluiu que a explicação deveria residir num qualquer tipo de oval. Finalmente experimentou a elipse: a simplicidade desta secção cónica devolvia resultados perfeitos com o Sol ocupando um dos focos da elipse descrita por Marte.

A Astronomia Nova, publicada em 1609 (uma das mais extraordinárias obras científicas de todos os tempos, que expende duas das três Leis dos Movimentos planetários; a terceira surge no Harmonices Mundi de 1618) é, como qualquer trabalho de Kepler, um exercício honesto e transparente, quase um diário científico das suas investigações nesses anos de 1602-1604. Ao contrário de Newton, explicou o processo, a metodologia, os erros e os recomeços, e reconhecia generosamente os contributos (algo em que Newton ou Copernicus foram sempre relutantes). E o que dizer de Galileu, sempre atento a honrarias e lucros?

Como Kepler concluiu, um planeta move-se mais depressa na sua órbita quando mais perto do Sol e mais lentamente quando mais afastado. Na ilustração (com a excentricidade exagerada), planeta demora o mesmo tempo a percorrer as distâncias A-B e C-D. (Ridpath, I., Skywatching (Go series), Hamlyn, 1987, p.13)

As Leis de Kepler
- A 1ª Lei descreve as órbitas dos planetas em torno do Sol, numa órbita elíptica, com o Sol num dos focos;
- A 2ª Lei assegura que o segmento de recta que une o Sol a um planeta varre áreas iguais em intervalos de tempo iguais;
- A 3ª Lei indica que o quadrado do período de revolução de cada planeta é proporcional ao cubo do raio (médio) da respectiva órbita. Portanto, quanto mais distante o planeta estiver do Sol, mais tempo levará para completar a translação.

A velha cosmologia baseada nas esferas e em modelos geométricos vinculados à necessidade do movimento circular será descartada em detrimento de uma visão física, dinâmica. É o grande salto qualitativo. Na batalha contra os equívocos epistemológicos do passado (os "axiomas" do movimento circular e do movimento uniforme), Kepler emerge como a grande figura da Nova Astronomia. Não existindo esferas nem "compartimentos", o amplo espaço vai acomodar as órbitas elípticas explicadas nas suas três Leis. A segunda destas conhecerá diversas formulações, sendo que Newton utilizará mais tarde aquela que doravante prevalecerá (conhecida como "lei das áreas"): "Num referencial fixo no Sol, a recta que une o planeta ao Sol varre áreas iguais em tempos iguais".

Todavia, é curioso verificar a complexidade de uma época na qual um matemático tão influente como Kepler é também, numa das suas facetas, "not a mathematician of the modern, Leibniz-Newton kind, but a Ficino-mathematician, of the Neo-Platonist, Cabalistic type." (Tester, Op. cit., p.233).

Kepler procurou avidamente princípios baseados na harmonia e na analogia. No Mysterium Cosmographicum (1596, adenda em 1621), num rasgo quase místico, investigou respostas integradoras relacionando os poliedros regulares teorizados no Timaios (os chamados Sólidos Platónicos: tetraedro, cubo, octaedro, dodecaedro e icosaedro) associados pela Física Aristotélica aos quatro elementos e ao quinto elemento incorruptível) com as órbitas planetárias, em busca do "Divino Plano". Encaixados e inscritos em orbes esféricos revelariam a base geométrica do Universo heliocêntrico. Há uma ressonância pitagórica mas Kepler estava a fazer algo mais: a articular a sua geometria com quantidades mensuráveis. Prezava ainda, talvez acima de tudo, as supostas harmonias musicais dos planetas (baseada nas proporções, não nas distâncias concretas), essência da "Divina Harmonia do Universo" (Harmonices Mundi, Linz, 1619). Uma música contínua, "a várias vozes", perceptível pelo intelecto, não pela audição. Para Kepler e seus contemporâneos, o mundo, como as Sagradas Escrituras, é um livro que canta a glória de Deus. Estas consonâncias e proporçóes harmónicas inseriam-se, todavia, ao contrário das da tradição pitagórica, numa framework heliocêntrica.

Como Pannekoek resumiu, assiste-se, doravante, e irrevogavelmente, a uma nova metodologia científica que se estende à generalidade das disciplinas:

"In Tycho Brahe’s and Kepler’s work the new method of scientific research is embodied — the method of collecting data from experimentand observation, and from them deriving rules and laws which form the body of science. They were not the only ones; at the turn of the century, in every field of knowledge, investigators appeared: Simon Stevin and Galileo studied mechanics, the laws of equilibrium and motion, Gilbert studied magnetism, Vesalius studied anatomy, Van Helmont studied chemistry, and Clusius studied botany." (Op. cit., p.242).

Com a Terra "deslocada" para a sua nova condição, o edifício teórico aristotélico deixou de explicar fisicamente os fenómenos. Antes, os elementos procuravam o seu "lugar natural". Agora as teorias prevalecentes do peso e movimento eram insuficientes, precisava-se de uma nova Física que explicasse os movimentos da Terra e porque é que os seus habitantes não sentem a "estonteante" sensação da velocidade. O De Revolutionibus de Copernicus não apresentava respostas. Seria necessário percorrer todo um percurso até Newton para responder a muitas questões e transformar a Astronomia de uma ciência de Geometria numa ciência da Física.

Aristóteles acreditava que qualquer corpo exigia uma força actuante contínua para perpetuar o seu movimento, e que somente poderia efectuar um único tipo de movimento de cada vez. A teoria já era contestada por alguns autores medievais. No início do século XIV, Jean Buridan afirmou que um corpo (e.g., um projéctil) não exigia a acção contínua e ininterrupta de uma força mas apenas um ímpeto ("impetus") inicial. Mais tarde, Galileu mostrou que, ao contrário do afirmado na doutrina aristotélica, os corpos de peso diferente caem à mesma velocidade. Também demonstrou que os corpos podem executar mais do que um movimento em simultâneo, e comprovou que o trajecto de um projéctil é uma curva (parábola) e não dois movimentos rectilíneos sucessivos. Mais tarde Newton estabelecerá as suas três Leis do Movimento, sendo as duas primeiras extensões das conclusões de Galileu. A primeira (a da inércia), também confirmada por Descartes, estabelece que um corpo perpetua o movimento ou a quietude a não ser que uma qualquer força actue sobre ele. Segundo Newton, dois corpos atraem-se com uma força cuja intensidade é inversamente proporcional ao quadrado da sua distância e directamente proporcional ao produto das suas massas. Foi o colapso da explicação aristotélica e a abertura de uma nova Física abrangente.

A "Nova Estrela" de 1572 em Cassiopeia, assinalada pela letra "I" (Brahe Tychonis [1573] Tychonis Brahe, Dani De noua et nullius aeui memoria prius visa stella, iam pridem anno à nato Christo 1572, Hafniae, Impressit Laurentius Benedict). Aquando da descoberta, estava (astrologicamente) no grau 7 de Taurus.

Quem criou (ou capitalizou) o telescópio foram os ópticos holandeses Hans Lipperhey (c.1570-c.1619) e Sacharias Janssen (1588-ca. 1630). Também o praticamente desconheciso Jacob Metius. Em 1608, Lippershey (a grafia correcta é Lipperhey) regista a patente de um instrumento "para ver coisas longe como se estivessem perto". A técnica de polir lentes para óculos (os chamados "occhiali") já se praticava em Itália em finais do séc. XIII. No séc. XV já se banalizara a utilização dos vidros colocados numa estrutura e pousados no nariz, com ainda usamos. Todavia, uma lente deste tipo não é um telescópio, que exige no mínimo duas lentes. A lente afastada deve ser convexa, como era a dos ochialli; a lente ocular, próxima do olho, pode também ser convexa (inverte a imagem) ou pode ser côncava. Há poucas referências fiáveis anteriores a Lippershey, que chamou kijker (observador) ou kijkglas ao novo equipamento, publicitando as suas vantagens no uso militar e naval, por exemplo. A sua disseminação foi célere. Galileo Galilei (1564-1642) chamou à sua invenção (i.e. adaptação) perspicillum (um neologismo latino). Em Italiano é chamado cannocchiale (vertido como canóculo em Português). Em França também era chamado "La lunette de Hollande".

A designação óbvia ("telescópio") foi criada três anos depois por Giovanni Demisiani. O esboço telescópico da Lua feito por Thomas Harriot e datado de 26 de Julho de 1609 é, provavelmente, o primeiro desenho de um corpo telescópico, precedendo Galileu quase quatro meses (Nick Kanas, Solar System Maps: From Antiquity to the Space Age, Springer/Praxis Publishing, 2024, p.146). Mas é Galileu quem inaugura a observação telescópica sistemática do céu. Descobre, em paralelo com Simon Mayr, latiniz. Marius (1573-1625), os quatro principais satélites de Júpiter (Medicea Sidera, como lhes chamará, os "Circulatores Jovis" de Hevelius; prevalecerão os nomes mitológicos escolhidos por Marius). Observa ainda as fases de Vénus e outros fenómenos (que, à maneira da época, vai divulgando em linguagem codificada, de modo a mais tarde defender a prioridade das suas descobertas (recorria-se à publicação de logogrifos e anagramas para salvaguardar a descoberta enquanto se investigava e confirmava). Galileu foi useiro e vezeiro neste método.

Retrato de Simon Marius, do seu Mundus Iovialis, 1614. Representa-se um telescópio e, em cima, à esquerda, um esquema de Júpiter e dos seus satélites

Um exemplo de Christiaan Huygens (1629-1695) é sobejamente conhecido. O planeta Saturno, na época o mais longínquo, era caracterizado como monosphaericus ou trisphaericus, pelo seu aspecto no telescópio. Huygens descobriu a natureza da sua verdadeira morfologia e utilizou um criptograma para divulgar a sua descoberta: "aaaaaaacccccdeeeeeghiiiiiiillllmmnnnnnnnnnooooppqrrstttttuuuuu". Era usual, como vimos, após descobrir algo que exigisse sequente investigação, recorrer-se a um anagrama (transposição de letras), evitando que alguém "roubasse" a primazia da descoberta. O cientista anunciaria-a laconicamente sob a forma de anagrama cujo significado só ele conhecia. Quando fosse conveniente, desvendaria o "segredo". Três anos depois, seguro da sua conclusão, Huygens revelou o enigma: Annulo cingitur, tenui, piano, nusquam cohaerente, ad eclipticam inclinato ("É rodeado por um anel, fino, plano, que não o toca em qualquer sítio, inclinado com a eclíptica"). O seu "Systema Saturnium" foi publicado em Julho de 1659 mas Huygens não manteve completamente em segredo a grande novidade, confidenciando e permitindo a revelação no ano anterior, num encontro da Académie de Montmor (Paris), v. Van Helden, A., "Annulo Cingitur": The Solution of the Problem of Saturn, JHA v (1974), 155-174.

Voltando a Galileu, note-se que a sua "carreira" observacional foi, como verificaram historiadores como Z. Kopal, de uma duração (surpreendentemente) curta: basicamente entre 1609 e 1611. Um trabalho breve mas muito consequente (desaprovando a natureza etérea e incorruptível da natureza do 'éter' aristotélico). Galileu abraça a visão heliocêntrica, que não conseguirá vindicar, mas contribui com as suas observações para a pulverização da crença num universo imutável.

Cynthiae figuras aemulatur mater amorum ("A mãe dos amores [Vénus] imita as figuras [fases] de Cynthia (Artemisa, Diana, i.e. da Lua). Foi assim que Galileu, resolvido o anagrama, divulgou a sua descoberta telescópica que provava que Vénus mostrava fases, ergo orbitava em torno do Sol.

Giovanni Borelli (1608-1679) continuará a desenvolver princípios de observação e testagem das hipóteses científicas (v. A. Koyré, The Astronomical Revolution: Copernicus-Kepler-Borelli, Cornell University Press, 1973). A médio prazo, a utilização de telescópios apontadores como instrumentos de medida (com tubos longos e pequenas aberturas, i.e. pouco brilho mas razoável ampliação) será importantíssima para a precisão das observações. O italiano Francesco Generini (1630) teve a ideia de utilizar um fio de mira no plano focal. O inglês Gascoigne (c. 1640) e ainda Montanari (de Bolonha) introduzem a utilização do micrómetro para aferir com rigor pequenas distâncias angulares entre duas estrelas. Os franceses Auzout e Picard, incorporam a utilização de círculos graduados nos telescópios. Deste modo, as medições das coordenadas tornam-se muito mais precisas (Abetti, Op. cit., p.126).

No século XVII, novos princípios filosóficos substituirão a tradicional doutrina aristotélica. Dois nomes se destacam na proclamação dos novos métodos da Ciência: Francis Bacon e René Descartes. O primeiro publicará em 1620 (com o eloquente e revelador título de Novum Organon, que evoca e afirma renovar o ponderoso conjunto das obras da lógica aristotélica), uma resoluta defesa da experimentação e pesquisa como alicerces únicos da Ciência e da Filosofia. O segundo destacará o princípio crítico e a dúvida metódica (avançando através de um processo que tem como regras: evidência, análise, síntese, enumeração).

René Descartes procura dar resposta aos novos problemas cosmológicos que se apresentam. Concebe a primeira formulação moderna das leis da natureza e de um princípio da conservação do movimento. A cosmologia de Descartes, inovadora, é descrita de um modo mais burilado nos seus Principia Philosophiae (1644). A teoria pressupõe um universo repleto, um plenum de matéria. A matéria e o espaço estão interligados (são essencialmente a mesma coisa) e obedecem a um conjunto de leis de movimento. O Universo é constituído por vórtices contíguos, gigantescos redemoinhos. As particulas movimentam-se, quando uma se desloca outra ocupará o seu lugar. Tudo está ligado, o Sol, menos denso, ocupa o centro de um vórtice, os planetas são mais pesados e perpetuam um movimento circular em torno do Sol. O plenum de matéria líquida de Descartes é que determina o movimento dos corpos, que de outro modo seria rectilíneo (e.g., os cometas movimentam.se em linha recta entre dois vórtices, sendo a órbita somente inclinada se entrarem num destes turbilhões). Abre-se a inovadora possibilidade de outras estrelas serem sóis e também centro de outros sistemas. Se o vórtice de uma estrela definhar (letra "N" na gravura seguinte), o astro pode caír num vórtice vizinho. Se aí permanecer torna-se um planeta. Caso se movimente para outro, passa a ser um cometa. Esta teoria engenhosa fascinou e contribuiu para abrir perspectivas cosmológicas futuras. Mas não prevaleceu.

Descartes considera três substâncias: a divina (eterna, perfeita e infinita. i.e. Deus), a substância pensante finita e dependente (res cogitans) e, finalmente, a matéria (res extensa). A Extensão é a característica essencial da matéria. A característica essencial ou atributo dos corpos é a extensão, quer dizer, o estar no espaço, com suas modificações ou modos: a quantidade, a forma e o movimento. Como consequência disso, os corpos submetem-se à quantidade e podem ser explicados em termos mecanicistas e a filosofia que os explica possui carácter obviamente matemático. Num argumento de tipo escolástico, o filósofo concluiu que uma vez que um 'atributo' somente existe como atributo de uma qualquer substância, não pode existir 'extensão sem matéria', ou seja, não pode haver vácuo. Em resumo, só havia um tipo de espaço e um tipo de matéria. O espaço não é variável em densidade, nem o é a matéria. Conclui que um espaço sem matéria - um vácuo - seria conceptualmente absurdo. Contudo, era uma abordagem conceptual.

Os vórtices ou "tourbillons": o Sistema Solar está representado no centro e inclui os orbes dos planetas. Os restantes rodeiam outras estrelas "fixas": ilustração representa ainda dois cometas. (Nicolas Bion, L'usage des globes celestes et terrestres, et des spheres, suivant les differens systemes du monde; précedé d'un Traité de cosmographie, 1700). [Clicar para versão completa c/ maior definição].

Contudo, a cosmologia cartesiana não havia sido formulada para poder ser imediatamente testada e comparada com observações concretas. E os seus "vórtices" não eram fruto de deduções a partir da observação. Os cartesianos podiam, por exemplo, procurar explicar o estado presente mas não podiam antecipar ou prever o posicionamento futuro dos corpos celestes, algo que a Física Newtoniana permitirá.

Em pleno século XVII permanecia a dúvida acerca da natureza da força que impulsionava o movimento dos corpos celestes. E. Brooke-Hitching (The Sky Atlas: The Greatest Maps, Myths and Discoveries of the Universe, Simon & Schuster UK Ltd., 2019) resume:

"The mystery that remained for astronomers of the mid-seventeenth century was the force that drove planetary movement. Kepler believed that, whatever this force was, it emanated from the Sun, the ‘soul’ of the universe, which bore similarity to Descartes’s torrid matter-filled system, where the celestial bodies were swept around on elliptical paths by a giant central solar vortex. Other theories were also in circulation. Kepler himself had been influenced by the work of the English physician William Gilbert, who in 1600 had published De magnete . . . (‘On the Magnet...’) in which he stated the theory that Earth was a giant attractive magnet. This explained the fall of objects back to the ground, and the behaviour of the magnetic compass."

Seriam turbilhões matéricos colidindo, análogos aos de Descartes? Mas o Universo de Descartes era caótico, com os corpos movimentando-se sem um comportamento previsível. Antes, como se lê na citação acima, Kepler ponderou uma energia 'magnética' que emanava do Sol. Foi influenciado por uma teoria publicada no De magnete (1600) por William Gilbert, que especulava que a Terra se comportaria como um gigantesco íman esférico, explicando assim a queda dos corpos e o comportamento da bússola. Mas em 1674 o prolífico Robert Hooke, ligado à Royal Society, publicou as suas influentes "suposições". A primeira propunha que os corpos celestes possuiam uma força atractiva que actuava não somente nas suas diferentes partes mas também sobre os outros corpos celestes. A correspondência entre Hooke e Newton demonstra que, em 1679, o primeiro compreendia melhor e estava mais receptivo à ideia abrangente da 'gravidade'. Essa "força atractiva", extensão da "filosofia magnética" de Gilbert e Kepler torna-se influente. E Hooke argumentou, numa palestra em 1674, que todos os corpos celestes possuem um poder de atracção ou "gravitação" na direcção do próprio centro, que lhes garante a morfologia e estrutura e também actua sobre os outros corpos que caem within the sphere of their activity ("na sua esfera de influência"). Uma sugestão auspiciosa. Mas será Newton (1642-1727), entretanto motivado, a conseguir resolver matematicamente, em três ou quatro anos, o problema das órbitas elípticas e a codificar matematicamente o importante avanço. Investigará as propostas de Hooke e ratificará a conclusão sugerida de que toda a matéria, desde uma pedra a um planeta, exerce esta misteriosa força, tudo dependendo do tamanho dos corpos e do quadrado inverso da distância, concluíndo que a Lei das Áreas de Kepler (a segunda) era uma consequência da acção de forças centrípetas.

Como Sir Edmund Whittaker explicou (From Euclid to Eddington: a Study of the External World, Dover, 1958, pp.11-2), existia uma teoria contemporânea rival da de Descartes, inspirada por Pierre Gassendi, religioso que leccionava no Collége de France. Gassendi devotou imensos esforços a tentar provar que a fé Católica não era incompatível com a filosofia Epicurista. Em oposição ao plenum cartesiano, defendeu a teoria de átomos movimentando-se no vazio, que Epicuro (c. 300 a.C.) havia (supostamente) adoptado de Leucipo e Demócrates (c. 400 a.C.). De acordo com a teoria, os elementos últimos da matéria são pequenos corpúsculos indivisíveis, variáveis no tamanho e na forma, mas não na sua constituição. A importância da perspectiva de Gassendi reside, em grande parte, no facto de ter sido adoptada por Newton. Uma perspectiva "atomista" e um espaço absoluto.

O paradigma do século XVII será "mecanicista". Existiam mecanismos cada vez mais complexos e a "filosofia mecanicista", também conhecida como "corpuscular" ganhava adeptos (e.g., Gassendi, Boyle, Huygens, Newton). Concebe-se a constituição da matéria (em oposição às teorías físicas aristotélicas) segundo uma inspiração atomista, adaptada às leis deterministas da mecânica de Galileu e Newton. Sustenta-se que as características dos corpos e seus fenómenos se explicam pelos movimentos de partículas (indivisíveis ou não, segundo os autores): os corpúsculos ou átomos.

"The outlook of the later Middle Ages had been dominated by Aristotle, and that of the Renaissance by Plato. But in the period following, the ‘mechanical philosophy’, alternatively known as the ‘corpuscular philosophy’, became increasingly attractive. It had originated with the Greek atomists, who explained the different qualities we perceive in the bodies around us as being the ways our senses interpret the movements of unchanging particles; and this appealed to an age that found a refreshing clarity about explanations that used concepts like speeds and shapes, concepts that were mathematical at least in principle." (Hoskin, The History of Astronomy, Op. cit., 2003, p.59)

Ou seja, depois da prevalência da interpretação aristotélica (que enforma toda abordagem até advento da Nova Ciência) e do fascínio renascentista com Platão (e, convém dizê-lo, com o Neoplatonismo, o Pitagorismo, o Hermetismo e toda a suposta "filosofia perene" (prisca sapientia)), doravante, com o interesse crescente numa "filosofia mecanicista" conhecida alternativamente como "corpuscular", redescobrem-se antecedentes "compatíveis" nas teorias dos chamados atomistas gregos (e.g., Leucipo, Demócrito) para os quais universo era composto por partículas indivisíveis chamadas "átomos" e pelo "vazio", sendo que os átomos, diferindo (somente) na forma, tamanho, combinação o movimento, formavam toda a diversidade de tudo o que existe.

Newton ficara, num primeiro, momento fascinado pela cosmologia cartesiana e será somente através dos estímulos das inovadoras sugestões de Robert Hooke e da verificação das já conhecidas Leis de Kepler que avançará do equivoco do plenum cartesiano para a concepção de um Universo "espaçoso" que obedece à gravitação (a mútua atracção entre os corpos celestiais, como Hooke supunha), doravante com carácter universal. As Três Leis de Newton (base para o entendimento do comportamento estático e dinâmico dos corpos) permitirão explicar os fenómenos do Sistema Solar, as marés, até prever o retorno de um cometa que celebrizará o influente Edmond Halley, que "decifrou" a sua periodicidade (Halley fez observações meteorológicas e magnéticas, mapeou marés e procurou explicar a direcção dos ventos e as monções como consequências da rotação terrestre, publicando as suas conclusões em 1686). A aberração da luz (provocada pelo movimento orbital da Terra, de que constitui prova ou evidência) e a nutação (que se deve a uma pequena oscilação periódica do eixo de rotação da Terra) devem ser tidas em conta para obter medições astronómicas correctas e efectivamente precisas: estas duas descobertas fundamentais devem-se a James Bradley (1692–1762), que foi Astronomer Royal a partir de 1742). Assim, tornou-se possível medir com aproximação na ordem dos segundos de arco (1" é uma quantidade muito pequena, representando 1/100mm num círculo com 2 metros de diâmetro).

Voltaire, nas suas "cartas escritas de Londres" (Lettres philosophiques ou Lettres anglaises, publ. 1734), comparou, com a sua habitual argúcia, as explicações cartesianas (ainda comuns em França) com as newtonianas, já aceites na Inglaterra, que serão vindicadas (v. Quatorzième Lettre, da edição de F. A. Taylor [Basil Blackwell, 1965], .PDF, 279KB).

Em plena revolta das colónias americanas, Thomas Paine (no seu "incendiário" panfleto Common Sense, de 1776), utilizou ideias e metáforas de inspiração newtoniana, prática comum nos precursores modernos da Democracia ("democrata", no contexto, tinha conotação pejorativa) e do Liberalismo (um anacronismo pois termo somente se começa a usar no século XIX). defendeu a Revolução Americana (que no início era mais um protesto do que uma manobra independentista) num discurso repleto de referências newtonianas, e.g., “In no instance hath nature made the satellite larger than its primary planet.”. Paine defendia a igualdade de todos os homens (ao contrário dos que defendiam que a representatividade dependia da propriedade e dos bens; Kant, por exemplo, chegou a sustentar que empregados e mulheres, por dependerem de outrém, careciam de personalidade civil), e era obviamente contra a monarquia (ao contrário de Hobbes que, apesar do pensamento de vanguarda, acreditava na necessidade de uma garantia de "coesão" contra a anarquia, na figura de um soberano; ou de Locke que somente salvaguardava que os poderes de um monarca deviam ser limitados). Paine foi uma figura interessantíssima e "inclassificável". Os princípios newtonianos terão uma influência decisiva tanto no Iluminismo como na posterior filosofia Positivista, no desdém pelas metafísicas e no primado da articulação entre observação e razão. As "ondas de choque" newtonianas estenderam-se a outras áreas, por exemplo às supostas "leis" da Psicologia (respaldadas em estatísticas) ou à Economia (Adam Smyth no seu The Wealth of Nations (1776) defende a não intervenção nos mercados, de modo a que os preços se acomodem "naturalmente").

A Mecânica é a ciência das forças e movimentos. Isaac Newton (1643-1727) publicou os seus Principia (Philosophiæ Naturalis Principia Mathematica) e compatibilizou a mecânica terrestre com a mecânica celeste, na sua Teoria da Gravitação Universal. Nas palavras de G. Abetti: "(...) Thereafter the celestial bodies were considered in a unit frame, subject to the same physical and mechanical laws. These laws could be applied to the study of the shape and movements of the planets, satellites, and comets, as well as to the study of the position and distribution of the stars in the Milky Way." (The History of Astronomy, Op. cit., p.10). Isto pressupunha a falência definitiva do modelo aristotélico das "duas naturezas" distintas (a dos céus incorruptíveis e a do mundo sublunar, dos quatro elementos, da geração e corrupção). Quando publicado (1687), o trabalho de Newton foi recebido com hostilidade no meio filosófico. A ideia de uma espaço e tempo absolutos e a "acção à distância" era entendida como uma "qualidade oculta" e a acção da gravitação no espaço vazio era algo que se antagonizava com o plenum cartesiano, ainda em voga. Efectivamente, a teoria de Newton, respaldada em complexidades matemáticas, comprovava os efeitos de uma força misteriosa que ainda não se podia explicar. Mas será gradualmente aceite.

Em relação às 'estrelas fixas', Newton manteve uma postura "teologicamente correcta" e inflexível, deixando-as de fora das suas investigações. Deus criou-as como um cenário ideal, de simetria, eventualmente intervindo para as manter assim. Newton tinha estas complexidades. Mas tarde, em 1802, Herschel, verificou que componentes de estrelas duplas previamente observadas por si, tinham entretanto alterado as suas posições. Seria a gravidade a força actuante? Somente em 1827 é que o Francês Félix Savary conseguiu confirmar que as duas estrelas do sistema Xi Ursae Majoris se moviam em órbitas elípticas em torno do centro comum de massa. Entretanto, a observação dos enxames ou aglomerados também conduzia à conclusão lógica do processo pelos quais estes se formavam, a saber: a força gravitacional. (The Cambridge Illustrated History of Astronomy, Op. cit., p.235).

Página de título da primeira edição (1687) dos Principia (Philosophiae naturalis principia mathematica; fonte: St Andrews University Library; For QA35.P8)

Bibliograficamente, a "trilogia" fundamental da chamada Revolução Científica é constituída pelo De revolutionibus orbium coelestium de Copernicus (1543), pela Astronomia Nova ΑΙΤΙΟΛΟΓΗΤΟΣ seu physica coelestis, tradita commentariis de motibus stellae Martis ex observationibus G.V. Tychonis Brahe de Kepler (Heidelberg, 1609) e pelos Philosophiæ Naturalis Principia Mathematica de Newton (1687). Antes, com o estímulo de Halley, Newton escrevera em 1684 a monografia De motu corporum in gyrum, codificando matematicamente o que os cientistas de vanguarda no séc. XVII já acreditavam que se verificava no movimento dos corpos numa órbita. Neste resumo incompleto, abordámos momentos fundamentais do percurso: o De Revolutionibus de Copernicus e os seus defensores, e.g., Rheticus, Regiomontanus, as observações mais precisas de Tycho (compiladas nas Tabulae Rudolphinae, as novas tabelas de Kepler dedicadas ao Imperador Rudolfo II), as Leis de Kepler que definem órbitas elípticas e não circulares, o desenvolvimento da observação equipada, bem como o desenvolvimento das leis do movimento e da inércia por Galileu e, culminante, a Gravitação Universal de Newton. A admiração pelo génio ficou grafada no "couplet" de Alexander Pope: Nature and nature’s laws lay hid in night.
God said, Let Newton be!, and all was light.

O enorme Newton era extremamente complexo. Segundo John Maynard Keynes (o célebre filósofo e economista), que teve acesso ao seu espólio, foi "o ultimo dos mágicos" (manuscrito-base do texto utilizado nas conferências do Trinity College e Royal Society Club, 1936; trad. João Zanetic, .PDF, 1.91MB).

Embrenhado em assuntos místicos, alquímicos e de cronologia bíblica, Newton acreditava na "ciência astronómica" do (mítico) Centauro Quíron e também que Pitágoras já detinha um conhecimento abrangente da mecânica do Universo, que transmitiu de modo encriptado. O sábio inglês personifica uma época de transição, paralelamente apto a descodificar as "verdades ocultas" na Natureza e nas Escrituras. Vide, por exemplo, Karin Figala, Newton's Alchemy, in: I. Bernard Cohen and George Edwin Smith (eds.), The Cambridge Companion to Newton, Cambridge University Press, 2004, 37; Josephson-Storm, J., The Myth of Disenchantment: Magic, Modernity, and the Birth of the Human Sciences, University of Chicago Press, 2017, p.43 et seq., ch. 2, passim). Não esqueçamos que o próprio Robert Boyle (1627-1691), um dos fundadores da Química, também foi um alquimista. [A Alquimia tradicional, com o seu labiríntico simbolismo e literatura repleta de metáforas e complexas imagens, era a demanda da chamada Pedra Filosofal (para almejar a Crisopeia, a transformação dos metais vis em metais nobres, e da Panaceia ou "elixir da vida", promotor da saúde). Uma prática do âmbito da Filosofia Natural que estabelecia uma hierarquia da matéria e se fundamentava na ideia de "gestação" (análoga à dos seres vivos) dos minerais e metais, que aconteceria no seio da Natureza e os faria evoluir no caminho da perfeição plena (e.g., os metais plenamente maturados seriam sempre metais nobres); bem como na correspondência Macroscosmo-Microcosmo (Quod est inferius est sicut quod est superius). As operações alquímicas (que em conjunto constituiam a Magnum Opus) eram faseadas e enalteciam processos como a destilação e o isolamento de uma substância primordial ou "quitessencial", a da Criação. Respaldava-se nas polaridades (ou complementaridades) e na ideia de aperfeiçoamento que o alquimista, emulando a divindade, precipitava ou acelerava, ajudando a Natureza no seu trabalho e aperfeiçoando-se espiritualmente em simultâneo. De resto, os elementos e os princípios dicotómicos e complementares do Mercúrio e do Enxofre (Sulfur) (interpretados simbolicamente) estão na sua base, bem como a cristalização no "corpo" (o Sal). A tria prima referida por Paracelsus. Encontra-se na Meteorologica (lib. III) de Aristóteles referência à origem dos minerais a partir de um "vapor aquoso" (da Água) e de um "fumo terroso" (da Terra), que foram ulteriormente associados nos textos da tradição hermética, nomeadamente os atribuídos a Geber (Jābir ibn Ḥayyān, autor do séc. VIII), aos dois referidos princípios "consagrados". Acresce que, já em Aristóteles, quando expurgada da 'forma' a matéria-base é sempre a mesma, uma matéria primeva. O filósofo postulava a já mencionada ideia de maturação (ou aperfeiçoamento) operada no seio da natureza.]

Modelo mecânico do Sistema Solar ("Orrery"). O primeiro destes 'planetários' foi, provavelmente, inventado sob o patronato de Charles Boyle (4th Earl of Orrery), daí o nome em Inglês. Demonstravam, de uma perspectiva externa, as revoluções dos planetas e, por vezes, dos seus satélites. Um Tellurium era um modelo "abreviado" que incluia somente o sistema Sol-Terra-Lua. De um modo interessante, estes mecanismos traduzem a percepção setecentista de um Universo enquanto mecanismo racionalmente concebido. (Detalhe do "Grand orrery" (Wh.1275), construído por George Adams, c.1750; Whipple Museum of the History of Science, Cambridge)

Um planeta em dois pontos da órbita. O vector "v" da velocidade é constante mas altera sistematicamente a direcção devido à aceleração "a" na direcção do Sol, no centro (Wyatt, Stanley P., Principles of Astronomy, Boston, Allyn and Bacon, 1964, fig. 7.7:1)

No início do séc. XVII surgem as tabelas de logaritmos, que muito facilitavam os cálculos (John Napier em 1514, Henry Briggs, que as adaptou ao sistema decimal e Adriaan Vlacq, que as completou e publicou em 1628 com a assistência de Ezekiel de Decker). Também se dissemina a utilização de fracções decimais. Antes da invenção dos logaritmos, o algoritmo conhecido como "Prosthaphaeresis", usado no final do século XVI e início do XVII, era a única maneira conhecida que podia ser largamente utilizada para rapidamente aproximar o resultado de uma multiplicação.

Numa interessante aplicação das novas ferramentas, o dinamarquês Ole Rømer (1644-1710), trabalhando no Observatório de Paris, verificou um desfasamento na observação dos eclipses das principais luas de Júpiter (particularmente nos da mais próxima do planeta, Io), relativamente às rigorosas previsões de G. D. Cassini, o director do observatório. Mostrou que a velocidade da luz, sendo enorme, era finita [essa velocidade era tradicionalmente considerada infinita, algo "instantâneo", e nem sequer ponderada até essa época.] O método: os eclipses dos satélites de Júpiter eram observados a partir da Terra adiante do timing previsto matematicamente quando o planeta (e os seu cortejo de "luas") estava mais próximo mas mais tarde do que o timing computado quando Júpiter se encontrava mais distante. Rømer concluiu logicamente que a luz demorava mais a chegar quando o planeta se encontrava no ponto mais afastado da sua órbita e o inverso quando estava mais próximo. Em 1676 extrapolou a velocidade utilizando o valor da Unidade Astronómica aceite na época (a média entre o afélio e periélio da Terra, ou seja, entre o ponto mais afastado e o mais próximo da órbita em torno do Sol). Chegou a um valor equivalente a cerca de 200,000 km/seg. (2/3 do real). Provou assim que esta velocidade era finita. Foi a primeira medida efectuada de uma quantidade universal.

Segundo alguns historiadores, e.g., Jan Teuber, Ole Rømer og den bevægede Jord – en dansk førsteplads? (2004), o próprio Rømer nunca publicou os resultados e a extrapolação foi feita por outros autores, nomeadamente por C. Huygens, a partir dos dados coligidos por Rømer.

O matemático francês Pierre-Simon, Marquês de Laplace (1749-1827) foi quem deu o nome de Mecânica Celeste ao conjunto das aplicações da teoria da gravidade, que descreve a força de atracção entre objetos com massa. Mas como funciona realmente esta força no espaço? Será necessário esperar por Einstein. Em todo o caso, esta foi uma época de progressos incomparáveis. O génio matemático deste mesmo Laplace ou de Johann Carl Friedrich Gauss (1777-1855), o mathematicorum princeps que abriu tantos novos campos de investigação matemática (contribuindo especificamente para a Astronomia com importantes trabalhos de mecânica celeste e teoria da determinação de órbitas). Também as observações e descobertas de William Herschel (o ocasional descobridor de Úrano que fundou a astronomia sideral, catalogando os objectos do céu profundo, prescrutando a estrutura da "Galáxia" em termos de distribuição das suas estrelas), ou o contributo importantíssimo dos trabalhos de notáveis como, por exemplo, Euler, Bessel, Lagrange ou F. G. W. Struve.

William Herschel foi um dos mais notáveis e incansáveis observadores de todos os tempos. Foi acompanhado pela sua irmã Caroline e seguido pelo seu filho John Herschel. E sabemos como este trabalho podia significar "immensi labores et graves vigilie", como já se queixava Paolo Toscanelli no século XV. Leonhard Euler (1707-1783) parece ter sido o primeiro a concluir que, como consequência da Lei da Gravitação Universal, um planeta não descreve "rigorosamente" uma elipse em torno do Sol mas ambos descrevem elipses em torno do centro de massa comum, o mesmo acontecendo com os planetas e seus satélites. Friedrich Wilhelm Bessel mediu a primeira medida da paralaxe trigonométrica de uma estrela, 61 Cygni, efectuada entre 1836 e 1838), chegando ao resultado de que a estrela estaria a 10,3 anos-luz do Sol. Joseph-Louis Lagrange estudou o "problema dos três corpos", envolvendo a interacção Terra-Lua-Sol, os movimentos dos satélites de Júpiter e é conhecido pelos chamados "Pontos de Lagrange" (ou "pontos de libração", que são pontos de equilíbrio para objectos de pequena massa sob a influência gravitacional de dois corpos massivos em órbita). A presença de matéria cósmica foi pressentida por Halley por volta de 1720 mas a primeira formulação científica de uma teoria de absorção interestelar deve-se a F. G. W. Struve em 1847. Struve baseou-se no mapeamento das estrelas em diferentes partes do céu levada a cabo por W. Herschel. O padre Angelo Secchi fez comentários tempestivos acerca da existência destas "massas", que interpretou correctamente como "nebulosidades escuras", em 1877 (v. Abetti, pp.292-93). Edward Barnard confirmará fotograficamente estas presenças e, em 1919, publicará o artigo "On the Dark Markings of the Sky".

Wright - An Original Theory or New Hypothesis of the Universe

Demócrito de Abdera (456-370 a.C.), em consonância com as suas ideias filosóficas, considerava a Via Láctea um conjunto de estrelas ténues e não uma nuvem ou um reflexo (antecipando-se dois milénios a uma explicação da sua natureza). Thomas Wright (1711-1785), que influenciará Kant e Lambert, foi um dos primeiros a sugerir um Universo hierarquicamente estruturado. Nesta ilustração, descreveu a Via Láctea como um de infinitos "sistemas estelares". (An Original Theory or New Hypothesis of the Universe, London, H. Chapelle, 1750)

Assim que se compreendeu que o Sol era uma estrela como tantas outras, astrónomos e filósofos começaram a procurar explicar a origem ou formação dos planetas como algo intimamente relacionado com essa estrela. Laplace, na sua Exposition Du Système Du Monde (1796) contemplou uma hipótese visionária para a origem do Sistema Solar: na chamada Hipótese Nebular (já esboçada pelo filósofo Immanuel Kant), o sistema evoluíra a partir de uma massa globular de gás incandescente revolvendo em torno de um eixo de rotação atravessando o seu centro de massa. Esfriando, contraiu-se. Anéis sucessivos saíram de sua periferia e, finalmente, condensaram-se para formar os planetas, enquanto o Sol representava o núcleo central remanescente. A hipótese constituía uma explicação racional para os movimentos planetários, que se situam aproximadamente num mesmo plano e se desenvolvem na mesma direcção. Segundo W. Ley (Watchers of the Sky: An Informal History of Astronomy From Babylon to the Space Age, Viking Press, 1964 (1963), p.461), as duas propostas eram, em rigor, diferentes: Kant postulava uma matéria original informe e caótica; a hipótese de Laplace começava com uma nebulosa primordial com uma concentração, um "sol", no seu centro. Todavia, os autores do séc. XIX associaram ambas as teorias: "Kant-Laplace".

Laplace apresentou essa hipótese com alguma reserva ou desconfiança (défiance), sem lhe atribuir a seriedade do trabalho inspirado pela observação e pelo cálculo: "Quelle est cette cause primitive? j'exposerai sur cela , dans la note qui termine cet Ouvrage, une hypothèse qui me paraît résulter avec une grande vraisemblance, des phénomènes précédens; mais que je présente avec la défiance que doit inspirer tout ce qui n'est point un résultat de l'observation ou du calcul." (Exposition..., V, ch. VI)

Mais tarde, já no séc. XX, James Jeans (1877-1946) elaborou uma teoria (que já tinha antecedentes) muito dinâmica, na qual um encontro entre o Sol e uma estrela "intrusa" que passava nas imediações resultou, devido à perturbação gravitacional, na libertação de uma "língua" de matéria que se estendeu do Sol. Após o afastamento da estrela, essa matéria fluida separou-se e cada uma das porções tornou-se gradualmente num planeta. A teoria revelou debilidades e foi sendo abandonada.

A origem do Sistema Solar (através da explosão de um proto-Sol), em diferentes etapas, segundo Emanuel Swedenborg. Assumindo-se como místico dialogante com anjos e demónios, a sua obra Prodromus Principiorum Rerum Naturalium... (Leipzig & Dresden, F. Hekelium, 1734) é, todavia, totalmente baseada nos princípios científicos rigorosos do empirismo.

A hipótese prevalecente da "nebulosa" foi mais tarde adaptada às então chamadas "nebulosas espirais" (as actuais "galáxias") entretanto observadas com maior detalhe estrutural através de telescópios cada vez mais potentes e que se acreditava serem sistemas planetários em potência numa fase da sua formação. Outras teorias surgiram entretanto mas tornava-se evidente que nas "nebulosas espirais" se enfrentava uma escala muito maior, mesmo não se sabendo ainda quão vasta. Surgiram opiniões no sentido de considerar estas espirais (particularmente a "nebulosa" de Andrómeda) como verdadeiros "universos" independentes.

Conhecida gravura do "Leviatã" de Parsonstown (Birr Castle, Irlanda), enorme reflector construído por William Parsons ou Lord Rosse (3rd Earl of Rosse) em 1845 (aqui retirada de The Story of the Heavens (Second Edition), Cassell & Company, 1886) de Sir Robert Stawell Ball). No desenho da direita, Lord Rosse representou a morfologia espiral da "nebulosa" M51, em Canes Venatici (Phil. Trans., vol 160, 1850). Foi a primeira "nebulosa espiral" identificada e ainda não se sabia que se tratava de um "universo-ilha", um longínquo objecto extra-galáctico. A partir do desenho passou a ser informalmente conhecida como Whirlpool ("Redemoinho"), M51 no célebre catálogo de Charles Messier

Desenvolvimentos no séc. XIX e no início do séc. XX. A transformação da Astronomia em Astrofísica

Assitiremos aos ulteriores avanços da instrumentação nos anos de oitocentos. Convém, antes de mais, recordar que na última década do século XIX se assiste a uma verdadeira "explosão" na Física: Raios-X, o átomo, a radioactividade. Ao longo so século foram sendo inventadas e adoptadas novas tecnologias (e.g., fotografia, espectroescopia/espectrografia) e novas metodologias para a determinação das distâncias cósmicas. Curiosamente, no século XIX, com a constatação do movimento ondulatório da luz, os físicos reabilitarão uma espécie de plenum na substância do éter. Como o estro de Lord Balfour referiu: "they invented the aether in order to provide a nominative for the verb ‘to undulate’" (Whittaker, Op. cit., pp.13-4). Paralelamente, desenvolve-se o estudo acerca da natureza do átomo. Mais tarde, percebeu-se que a Galáxia não era 'única' (algo pressentido por pensadores pretéritos como Kant, no séc. XVIII, e finalmente comprovado pelas investigações do redshift detectado no espectro da luz proveniente das galáxias por Edwin Hubble em 1924).

"In 1750 Thomas Wright of England conceived of the Milky Way as a finite and flattened assembly of stars and speculated that it was not isolated in space. He believed that the little dim clouds were other similar stellar systems, far away and unresolved. In 1755 Immanuel Kant, the German philosopher, extended Wright’s notions to the theory of island universes. Assuming the Milky Way to be a circular disk of stars and other Milky Ways to be strewn at random far from each other in space, Kant reasoned that some such disks would be seen edge-on as highly elongated ellipses and that others would be seen face-on as circles. He also pointed out that the nebulae could not be resolved into individual stars because of their enormous distances. Nevertheless, the disks themselves were big enough to appear not as points but as patches of finite angular size. The ideas of Wright and Kant accounted for the observations of nebulae in a rational way, but proof of their general validity had to wait nearly two centuries for the construction of great reflecting telescopes." (Wyatt, Principles of Astronomy, Op. cit., p.484).

Henry Draper (1837-1882), pioneiro da astrofotografia, junto de um refractor equipado para fotografia astronómica nos anos de 1860 ou no início da década seguinte (Hastings Historical Society)

Quanto à fonte da energia do Sol e das restantes estrelas, a pista fundamental foi descoberta independentemente em 1938 por dois astrofísicos: Hans Bethe e Carl von Weizsacker. Resumidamente, o hidrogénio é transformado em hélio e energia é libertada nesse processo. É a origem da radiação do Sol. Como sabemos, o hidrogénio é a substância mais leve e abundante do Universo.

Se a energia do Sol tivesse origem na combustão química, não poderia ser mantida por mais do que alguns milénios. No século XIX, Lord Kelvin (William Thomson) e Hermann von Helmholtz sugeriram que o astro gradualmente se comprimia, libertando energia nesse processo e assim explicando a energia expelida ao longo de milhões de anos. Daqui se inferia que o diâmetro deveria diminuir ao longo desse período. Somente mais tarde, após a descoberta da radioactividade (por Henri Becquerel em 1896), se abria caminho para o posterior entendimento da verdadeira natureza do que acontece no Sol (e nas outras estrelas).

Francisco da Costa Lobo (1864-1945), do Observatório a Universidade de Coimbra será entre nós pioneiro e terá um papel fundamental na internacionalização da nossa astronomia, na abertura à Astrofísica e às novas tecnologias entretanto utilizadas (Vitor Bonifácio, “Costa Lobo (1864-1945), the Coimbra Spectroheliograph and the Internationalisation of Portuguese Astronomy”, Cahiers François Viète [Online], III-3 | 20; aceder),

O estudo do Sol, a estrela mais proxima, será, sem surpresa, a motivação para o aparecimentto da Astrofísica. Joseph von Fraunhofer (1787-1826) concebeu um instrumento composto por vários prismas, óptica de colimação e uma fenda fina e alongada, através da qual podia passar a luz. Com este, estudou o Sol. A par do químico William Hyde Wollaston (1766-1828), será pioneiro na revelação do espectro e dos chamados raios de absorção. Fraunhofer foi o primeiro a obter e medir comprimentos de onda das linhas do espectro solar. O estudo da composiçao da luz havia começado, em termos científicos, com Newton. Na imagem, um desenho do próprio Fraunhofer representando linhas do espectro solar e assinalando, em cima, curva de intensidade em diferentes zonas (H. Roscoe, Spectrum Analysis, London, 1870). Um princípio fundamental é o da uniformidade da natureza: tal como as leis de Newton se aplicam universalmente, também as leis que determinam o comportamento do Hidrogénio, do Cálcio e dos restantes elementos. O espectroscópio pode pois, como diz Allan Chapman, "trazer as estrelas distantes para serem estudadas no laboratório". Dezenas de milhares de spectra estelares estarão disponíveis por volta de 1910 e serão pacientemente analisados e elucidados por técnicas altamente qualificadas como Williamina Fleming, Antonia Maury ou Annie Jump Cannon.

Esquema dos componentes principais de um espectroscópio, por Gustav Kirchoff: o tubo "A" é um colimador óptico que tem no foco uma ranhura cuja largura é ajustada por meio de um parafuso; esta pode ser iluminada por uma fonte de luz (e.g., a imagem de uma estrela). O feixe de luz paralelo passa através dos sucessivos prismas (no exemplo vemos quatro prismas, que habitualmente eram de vidro espesso ou quartzo; cada um dispersava mais a luz recolhida, resultando num espectro maior com linhas de Fraunhofer mais conspícuas e fáceis de medir). Os raios são tanto mais desviados quanto mais elevada é a sua frequência. A luneta ("B"), que se move ao longo de um disco, permite observar os diferentes comprimentos de onda da luz dispersada. (Untersuchungen über das Sonnenspectrum und die Spectren der chemischen Elemente, 1, Berlin, 1862). A ilustação seguinte, um desenho de Allan Chapman, explica o funcionamento básico do espectroscópio (Comets, Cosmology and the Big Bang - A History of Astronomy from Edmond Halley to Edwin Hubble, Lion Hudson, 2018, fig. 17.1). Quando, ainda no séc. XIX, se acoplou uma câmara ao espectroscópio surgiu o espectrógrafo, capaz de captar a imagem do espectro analisado)

Henrietta Leavitt (1868-1921) verificou que determinadas estrelas variáveis com o mesmo período que estudou na região da chamada Pequena Nuvem de Magalhães tinham a mesma magnitude aparente. Assim, sabendo que estas estavam todas praticamente à mesma distância do Sol, extrapolou que todas as estrelas desse tipo, com o mesmo período de variação, deveriam ter a mesma magnitude intrínseca. Descobriu pois a importante relação luminosidade-período de variação destas estrelas pulsantes. Harlow Shapley demonstrou que esta relação era típica de um determinado tipo de variáveis de curto período, cujo modelo mais conspícuo era a estrela Delta da constelação Cepheus (δ Cephei), cuja regular variabilidade havia sido documentada pelo Inglês John Goodricke em 1784. As variáveis Cefeidas, pela sua previsibilidade, tornar-se-ão um cómodo e eficiente método para a medição de longas distâncias, autênticas "velas-padrão", pois quando detectadas em objectos distantes, a relação do seu brilho aparente e periodicidade permite calcular a sua luminosidade absoluta (Emilio Segrè Visual Archives, Shapley Collection, Physics Today Collection, Niels Bohr Library & Archives, AIP; photograph, Margaret Harwood). O diagrama à direita foi apresentado por Leavitt no seu importante paper (Harvard Circular, no. 173, 1912). Em 1952, Walter Baade (1893-1960) descobriu que existiam, na verdade, duas populações de Cefeidas (as "clássicas" e as de tipo II). Isto redundará na correcção dos resultados anteriormente obtidos.

E a teorização do nascimento, vida e morte das estrelas abrirá perspectivas cosmológicas antes insuspeitadas. Uma classificação abrangente das estrelas da Galáxia em "populações" (Population I, II e uma hipotética III, mais antiga e que já não podemos observar) foi gizada pelo mencionado e influente W. Baade em 1944, desenvolvendo uma ideia já avançada anteriormente por Jan Oort. Esta classificação das estrelas baseia-se em características como a sua localização, tipo de órbita no sistema galáctico e elementos pesados presentes na sua constituição ("metalicidade"). Estas características dependem da idade da Galáxia quando as estrelas se formaram, pelo que as "Populations" I, II e III contém estrelas que se formaram em épocas progressivamente mais recuadas.

O Universo expande-se e ganha tridimensionalidade quando analisado em etapas sucessivas, da Geometria à Física, como J.-P Verdet explica [resumo traduzido]:

O ponto de partida é o Sistema Solar; o método é geométrico e a base é a órbita da Terra: em intervalos de seis meses, a Terra ocupa duas posições separadas por 300 milhões de quilómetros. Permite medições de paralaxe. Na etapa seguinte, a base utilizada é o deslocamento aparente do Sol em relação a certas estrelas, determinando a velocidade aparente na esfera celeste (de afastamento ou aproximação), usando o efeito Fizeau-Doppler, percebendo as direcções nas quais as estrelas aparentam mover-se (o movimento próprio das estrelas havia sido descoberto em 1718 por Edmond Halley). A terceira etapa utilizou a física das estrelas: o brilho aparente, ou magnitude m, de uma estrela é uma função do seu brilho absoluto, ou magnitude absoluta M, e da sua distância. Surgem catálogos baseados na análises do espectro das estrelas (coligidos no Harvard College Observatory), bem como a esquematização desenvolvida independentemente por Hertzsprung e Russell, patente no diagrama hoje identificado pelos seus nomes. Em 1912, Henrietta Leavitt publicou um artigo onde apresentou a relação matemática relacionando o período e a magnitude aparente de um determinado tipo de estrelas variáveis (as Cefeidas, nomeadas segundo o exemplar "típico" originalmente estudado: a estrela Delta Cephei). Tinha acabado de descobrir uma nova maneira de relacionar a magnitude aparente com a absoluta e, portanto, conhecer a distância. Tornou-se possível determinar a distância de um objecto onde se encontre uma cefeida. Posteriormente, E. Hertzprung estudou as distâncias destas variáveis estatisticamente, a partir dos seus movimentos próprios. No passo seguinte, verificou-se que o espectro luminoso de um astro nos dá a sua velocidade radial. Move-se para o violeta se a estrela se aproxima, para o vermelho se ela se afasta. Este fenómeno de grande escala (teoréticamente interpretado como um efeito Doppler) permitiu retirar ilacções quanto às distâncias e, consequentemente, quanto à expansão do Universo. É ao trabalho de V. Slipher, E. Hubble e M. Humason que devemos a determinação das maiores distâncias acessíveis. (Une Histoire de l'Astronomie, op. cit., Troisième partie, 3, 4).

Refira-se também, na estimativa de distâncias, a relação entre o período de pulsação e a magnitude absoluta das estrelas do tipo RR Lyrae (a "estrela modelo" situa-se na constelação boreal de Lyra), que as transforma em excelentes velas padrão, particularmente no interior da Via Láctea.

Na imagem superior, o chamado método das Paralaxes Estatísticas observa a convergência aparente, num ponto do céu, das estrelas de um mesmo enxame estelar que se afastam de nós (reparar na analogia com o efeito de perspectiva); em baixo, o efeito Doppler-Fizeau descreve a alteração no comprimento da onda emitida por uma fonte em movimento ou medida por um observador em movimento, em função da velocidade relativa fonte-observador. (ilustr. retiradas de: Roy, Jean-René, L'Astronomie et son Histoire, Presses de l'Université du Québec/Masson, 1982)

Este entendimento do Universo é relativamente recente. Em 1914, Arthur Stanley Eddington, que virá a ser um dos mais importantes astrónomos da primeira metade do séc. XX, ainda era obrigado a reconhecer: "Direct evidence on whether the spiral nebulae are within or without our stellar system is completely lacking." (Stellar Movements and the Structure of the Universe). Até 1915, o sistema da Galáxia estava ainda em conformidade com o chamado modelo "Herschel-Kapteyn", com cerca de 1000 a.l. de diâmetro e cerca de 3000 a.l. de espessura, com concentração num plano e na direcção do centro. As primeiras indicações quanto à rotação deste sistema datam já de 1922 (por E. F. Freundlich e E. von den Pahlen) mas foi somente comprovado através do trabalho de Lindblad e Oort estudando os diferenciais nos movimentos de estrelas próximas. O Alemão Carl Wirtz (1876-1939) foi o primeiro a sugerir (em 1924) que os redshifts medidos no espectro das "nebulosas extra-galácticas" (como então se designavam as galáxias) seriam deslocamentos 'Doppler' indicativos de movimentos radiais (Kopal, Op. cit., p.148)

Hoje sabemos que as galáxias são as unidades organizacionais básicas do Universo. Supõe-se que as nuvens de hidrogénio e hélio (os elementos químicos leves, produzidos no Big Bang) se condensaram para formar as primeiras gerações de estrelas que, agregando-se, criaram estruturas comparáveis ou mesmo similares aos enxames globulares. Estas coalesceram em galáxias. Nestas, a fusão nuclear em estrelas maciças deu origem a elementos químicos mais pesados, libertados através da explosão de supernovas no medium interestelar. Nas nuvens de gás e poeiras assim formadas, nasceram e nascem as novas gerações de estrelas.

Demais, o Universo surge em expansão e ganha dimensões avassaladoras. A recessão é mais evidente quanto mais distantes estão as galáxias observadas. Os estudos pioneiros são publicados por Vester Slipher no Lowell Observatory e Edwin Hubble, cujo primeiro paper descrevendo a relação entre redshift (desvio para o vermelho no espectro electromagnético) e distância (comprimento de onda proporcional) data de 1929. Também uma referência a Ernst Öpik (1893-1985), que publicou, antes de Hubble, um paper com uma estimativa da distância da galáxia de Andrómeda (com maior aproximação do que a do astrónomo americano) e também demonstrando a sua exterioridade relativamente à Via Láctea (entre outras descobertas relevantes, e.g., a chamada Nuvem de Öpik-Oort, hipotética região esférica de planetesimais voláteis na periferia do Sistema Solar, onde se acredita estar a origem dos cometas).

Um notável precursor da teoria de suporte ao modelo cosmológico prevalecente foi Georges Lemaître (1894-1966). Este sacerdote e astrónomo havia sugerido, em 1927, ainda antes da constatação da expansão do Universo por Edwin Hubble, a possibilidade teórica de compreender retrospectivamente um Universo em expansão, recuando no tempo até ao ponto a que chamou "Átomo Primevo".

As conhecidas teorias de Albert Einstein (1879-1955) têm como antecedente (por analogia) as elucubrações de Michael Faraday (1791-1867) e James C. Maxwell (1831-1879), que relacionaram a electricidade, o magnetismo e a luz num mesmo fenómeno, o campo electromagnético. Einstein, por seu lado, estuda o campo gravitacional e publica a sua Teoria Geral da Relatividade em 1915. Abrirá perspectivas cosmológicas e abalará o nosso anquilosado entendimento das categorias do espaço e do tempo.

Albert Einstein (1879-1955) com alguns cientistas americanos (o segundo é Edwin Hubble; seguem-se St. John, Albert Michelson, o próprio, William Campbell e Walter Adams). Crédito: Carnegie Institution of Washington, Pasadena (in: Sugimoto, Kenji, Albert Einstein: A Photographic Biography, Schocken Books, 1989)

Numa sugestão absolutamente genial, Einstein afirma que o campo gravitacional não é uma característica do espaço, é o próprio "espaço-tempo", um "material" em si mesmo, um "tecido" que nos rodeia e que é deformado pela massa dos corpos. O espaço-tempo associa o conceito do espaço geométrico de três dimensões com o contínuo temporal unidimensional. Substitui as pretéritas noções autónomas, sendo doravante o cenário comum dos fenómenos físicos. A Teoria da Relatividade Restrita de Einstein estabelece o carácter "não absoluto" do Tempo (dilatação: os intervalos de tempo marcados por um observador em repouso são sempre maiores que os intervalos de tempo marcados por um observador em movimento com velocidade aproximada à da luz) e a sua associação com o movimento, portanto com o Espaço. Na Relatividade Geral, a gravitação surge como propriedade geométrica do espaço-tempo. Explica ainda como a matéria e a energia deformam o espaço-tempo e como os objectos se movem segundo essa nova geometria.

O espaço-tempo deforma-se quando existe matéria. Como exemplo, o Sol deforma o espaço em seu redor e assim determina o movimento dos planetas. A luz também é afectada, permitindo estudar a magnitude do efeito lenticular que é a curva provocada pela gravidade quando a luz de um objecto distante é desviada por outro mais próximo, como foi comprovado pela primeira vez no célebre eclipse total de 1919, e desde então inúmeras vezes.

Em 1936, Karl Jansky (1905-50) descobre de modo fortuito a radiação rádio proveniente da Via Láctea (especificamente da região de Sagittarius) e abre o caminho para o desenvolvimento da Radioastronomia (imagem da antena direccional e rotativa utilizada; fonte: Bell Telephone Laboratories). Em 1944, o engenheiro Grote Reber (1911-2002) escreveu um artigo científico que expunha a detecção de radiação rádio no Sol. Localizou, ulteriormente, intensas fontes de rádio em Cassiopeia e em Cygnus (a poderosíssima galáxia Cygnus A é uma das mais fortes fontes rádio que conhecemos). Se no 'visível' detectamos facilmente as fontes mais poderosas, convém não esquecer que o mapa do céu é muito diferente noutras frequências do espectro electromagnético.