| A S T R O N O M I A |
|
|
|
descrição e sistemas de coordenadas
"O céu é esférico e move-se esfericamente" (Almagesto, I.2). Esta é a premissa fundamental da astronomia grega. Embora se fundasse, por vezes, em especulações de natureza filosófica ou mesmo mística, era também sugerida pela observação do céu. James Evans (The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p.75), afirma que para um observador mais inocente, o céu parece uma abóbada. Os antigos Egípcios representavam-no por um hieróglifo que parecia sugerir um edifício estilizado, com um tecto extenso e baixo. Contudo, embora as estrelas em si mesmas não nos forneçam pistas relativamente à morfologia do céu, os seus movimentos sugerem, de facto, que se trata de uma esfera: uma esfera enorme mas não infinita, o "maggior corpo" de Dante (Paradiso, 30.39). As estrelas deslocam-se em círculos paralelos, ascendem no oriente, culminam e descem no ponto oposto. Ainda mais sugestivo é o movimento das estrelas circumpolares, descrevendo os seus círculos em torno de um ponto específico. O tratado Περὶ κινουμένης σφαίρας (Perí kinouménis sphaíras: "da esfera em movimento") é o mais antigo tratado matemático completamente preservado que temos da Grécia antiga. O seu autor, Autólico de Pitane (Αὐτόλυκος ὁ Πιταναῖος) foi contemporâneo de Aristóteles. Os
modelos matemáticos mais antigos (Autolycus [c.330 a.C.], Euclides
[c.300 a.C.] e Theodosius [c.100 a.C.]) que elencam as propriedades e
movimentos da esfera, demonstram como o conceito pode explicar os
padrões variáveis dos nascimentos e ocasos do sol e das estrelas, bem
como a diferença de duração dos dias ao longo do ano. [Refere-se aqui o dia artificial, intervalo entre o nascimento e o ocaso do Sol (o dia natural era resultado do movimento diurno da esfera celeste e corresponde na realidade, como sabemos, ao período de rotação do nosso planeta).] Como Elly Dekker
resume (Illustrating the Phaenomena: Celestial Cartography in Antiquity and the Middle Ages,
Oxford University Press, 2013, p.5), o conceito tornou-se parte essencial das
teorias cosmológicas de filósofos como Platão e Aristóteles, e não mais
deixou de o ser: "The model of the rotating sphere provided a mathematical definition for the axis of rotation of the sphere of the universe and its extremities, the northern and southern celestial poles. Connected with this polar axis are series of parallel circles perpendicular to it (the Equator, the tropics and the ever-visible and ever-invisible circles), a series of semicircles extending from pole to pole (colures) and the so-called oblique circles (the ecliptic and the horizon). [...] The apparent daily motion of a star takes place along a fixed parallel. Its intersections with the horizon are its points of rising and setting." (Dekker, 2013, loc. cit.). Essa concepção resultou no chamado "modelo de duas esferas" (v. Bowen, A. & Goldstein, B., A New View of Early Greek Astronomy, Isis, vol. 74, No. 3 [Sep. 1983], p.333), no qual a esfera interior representa a Terra e a exterior o orbe das estrelas fixas. É, ainda hoje, o esquema privilegiado em qualquer abordagem didática da astronomia esférica.
Todos estes círculos eram uma ficção conveniente. Francisco Vicente de Tornamira explicava: "...es cosa puesta en razon que en el cielo no ay ningunos circulos ni orbes, sino que son fingidos y inventados con mucho cuydado y ingenio por los doctos y antiguos Astrologos, junto con el cortamiento de muchas lineas y figuras solo para dar nos a entender y enseñarnos los diversos movimentos de los cuerpos celestes, y sus aparencias y lugares, que sin esto no lo podian hazer. Lo qual ha sido negocio de mucha industria y aprovechamiento: de manera que lo podamos con demonstraciones ver con los ojos, y tratar con las manos como en Reloxes, y en los Astrolabios, Spheras y otros instrumentos mathematicos, que mas parece cosa divina que humana. Necessaria fue pues la invencion de los Epiciclos, Eccent[r]icos, auges y deferentes: y la variedad de los circulos y lineas que se hallan en las Theoricas de los Planetas, lo qual todo a causa que toda ça machina celestial es cõntida, se ha de entender que es imaginado y artificio o para buscar los ditos movimentos, os segun se ha dicho: dela suerte que en la Hydrographia, y arte de marear las lineas de los vientos, y rumbos q estan en las cartas para hazer la navegaciõ. En la Geographia las climas y parallellos, y sus distinciones para el sitio de los lugares, y variedad de las horas. Y en la Cosmographia, la posicion de las Zonas para enseñar los temperamentos de las regiones, con que diremos que todas las diversidades de circulos que dizé que ay en el cielo son ymaginarios, a si por su muchedumbre, como porq[ue] no vemos sus cuerpos, como [vemos] los de los planetas." (Chronografia, Repertorio de los Tiempos..., Pamplona: Thomas Porràlis de Savoya, 1585, pp- 21-22) Deste modo, o globo (spera solida) constituía no passado uma poderosa ferramenta pedagógica. Representava o Universo e a sua utilização evitava o conhecimento das minudências trigonométricas. Os exemplares mais antigos baseavam-se numa estrutura 'eudoxiana', com os coluros passando no meio (e não no início) das respectivas constelações zodiacais e ainda sem a divisão duodecimal da eclíptica (Dekker, Op. cit. p.432).
Esquema em corte representando os círculos fundamentais (paralelos e oblíquos) para uma latitude de 36º N. A "esfera local" inclui os dois paralelos que limitam (respectivamente) o céu circumpolar (sempre visível) e o céu sempre invisível. Os círculos oblíquos são dois: o Horizonte e a Eclíptica. (Dekker, ibid., p.6)
A Sphaerica, a teoria da esfera (Lat. sphaera; "sphaira", translit. do Gr. σφαίρα) e dos seus círculos, aplicava-se particularmente à Astronomia e à descrição do céu e dos fenómenos resultantes da sua rotação diária, nomeadamente os nascimentos e ocasos das estrelas. Uma disciplina utilizada ao longo dos muitos séculos desde a sua origem grega. Segundo A. Pannekoek, era parte da Geometria, a ciência das linhas e ângulos, círculos e outras figuras, suas relações e propriedades, doutrina teorética estudada e cultivada pela sua beleza intrínseca (A History of Astronomy, Dover Publications, 1989 (1961), p.159 [trad. nossa]). Um "monumento" às verdades abstractas: "If we call Greek astronomy the oldest, indeed the only real, natural science of antiquity, we must add that it was geometry materialized; the only field, truly, where geometry could materialize." (ibid.). A esfera enquanto instrumento constitui o expediente técnico mais óbvio: a alcora, do Ar. "der-alcorçi" segundo os Libros del Saber... editados por M. Rico y Sinobas em 1863-7). a "esfera del trono de las estrellas", i.e. o globo celeste. Entre nós, chamavam-lhe poma ou espéra. Reduzida à sua estrutura fundamental resulta na armilar (de "armila", "er-alhalac", segundo os Libros). Na Índia, os globos eram conhecidos como golayantra ("máquina-globo") ou golabandha ("banda" ou "faixa-globo").
Esfera
armilar "Santucci" (detalhe). Construída entre 1588 e 1593, esta esfera
de grandes dimensões e profusamente decorada foi encomendada por
Ferdinando I de' Medici (Grão-Duque da Toscânia), dela ficando encarregado Antonio Santucci. Representa a "Máquina do Universo"
segundo o modelo ptolomaico. Museo Galileo, Florença (Inv. 714)
A ideia de um Universo esférico pode ser atribuída a filósofos dos séculos VI e V a.C., como Pitágoras ou Parménides. Mas o primeiro que manifesta um entendimento claro e completo da Esfera Celeste é Eudoxus (Εὔδοξος, c. 370 a.C.), Desde o séc. IV a.C. que a esfera ["artificial" ou "matemática" como mais tarde se dirá] constitui a base para o entendimento dos fenómenos celestes observáveis. Como referido, os primeiros tratados acerca das propriedades e movimentos da esfera recuam a Autolycus (c. 330 a.C.), Euclides (c. 300 a.C.) e Theodosius (c. 100 a.C.), e demonstram como o conceito pode explicar os padrões variáveis dos nascimentos e ocasos ou a variação da duração dos dias e das noites. As medições precisas parecem recuar à época de Timocharis (Τιμόχαρις, primeira metade do séc. III a.C.) e Aristilo (Ἀρίστυλλος, c. 270 a.C.), como provado pela informação disponível acerca das declinações estelares (Dekker, op. cit., p.10). O desafio matemático da esfera tornar-se-á evidente: na superfície de uma esfera trabalha-se com senos, cordas e raios, não com linhas rectas.
Concomitantemente, alguns relatos "extravagantes" perpetuavam dúvidas ou curiosidades respaldadas em perspectivas arcaicas. Como J. L. E. Dreyer (A History of Astronomy from Thales to Kepler, reimpr. Dover, 1953 [1905], p.172) exemplificou [trad. nossa]: "...não nos devemos surpreender que um escritor crédulo como Ctésias [médico e historiador natural de Cnido radicado na corte do persa Artaxerxes II, autor de uma "Indica" e de uma "Persica", a primeira exclusivamente baseada em relatos indirectos], no início do século IV [a.C.] pudesse reportar que a partir de certas montanhas na Índia o Sol se via dez vezes maior do que na Grécia, ou que Posidónio condescendesse em refutar a ideia popular entre os habitantes das costas atlânticas de que o Sol se punha no oceano com um barulho sibilante [referência encontra-se em Estrabão: Geogr. [Geōgraphiká], III, 1, 5, apud Posidonius (cf. Posidonius 1: The Fragments (ed. L. Edelstein & I. G. Kidd), Cambridge, 2nd ed., 1989, Fragm. 119)], bem como o testemunho de Artemidoro de Éfeso [um adivinho do séc. II a.C.] de que em Gades [actual Cádiz] o Sol, no seu ocaso, parecia ter cem vezes o tamanho habitual [Estrabão, ibid (pp.8-11 no 2º vol. da ed. Loeb, 2006 (1923)]. Também não é estranho que o poeta Lucano faça o Atlântico ao largo da costa ocidental da Líbia [i.e. África] ser aquecido pela descida do Sol, enquanto as nuvens empurradas pelos ventos de leste através da Espanha [i.e. Península Ibérica] são travadas pela abóbada sólida do céu. Mesmo Virgílio [Publius Vergilius Maro], quando descreve o curso do Sol através do Zodíaco, tem dúvidas se no outro hemisfério "o silêncio da noite reina para sempre e a escuridão se adensa sob o manto da noite, ou se a Aurora vem até nós de lá ao mesmo tempo em que a luz avermelhada vespertina acende ali os seus últimos fogos. [Georg. I, linhas 247-251: Illic, ut perhibent, aut intempesta silet nox, semper et obtenta densentur nocte tenebrae, aut redit a nobis Aurora diemque reducit; nosque ubi primus equis Oriens adflavit anhelis, illic, sera rubens accendit lumina Vesper]."
Descrição da Esfera no Opusculo de Astrologia en medecina, y de los terminos y partes de la Astronomia necessarias para el uso della...,
de Juan de Figueroa, 1660. O autor refere a "esfera substancial", dividida em
10 "céus" (ou 11, com o undécimo "Empíreo" teológico) e a "esfera
acidental" ou local (i.e.
localização geográfica concreta). dividida em duas partes pelo
Horizonte. Explica a diferença entre os lugares que se situam no
"horizonte recto" (geograficamente situados no Equador Terrestre, com
ambos os pólos da esfera situados sobre a linha de horizonte e onde o
Equador Celeste faz ângulos rectos com o horizonte) e os restantes,
que se situam na chamada "Esfera Oblíqua" (um dos pólos está
sempre sobre o horizonte, outro sempre abaixo, e o Equador Celeste faz
com o horizonte ângulos que não são rectos: um é agudo e outro obtuso).
Refere-se obviamente aos ângulos segundo os quais o Equador Celeste
"corta" a linha de horizonte nas latitudes para norte e sul do Equador. Estes determinam a
ponderação dos tempos ascensionais segundo "ascensões rectas" ou
"ascensões oblíquas", respectivamente (v. infra). O texto elenca, seguidamente, os
10 círculos que se imaginam no côncavo e
no convexo da Esfera: 6 grandes círculos ("magnos": a "Equinocial", i.e. Equador, o "Zodíaco", i.e.
a Eclíptica, os Coluros Solsticial e Equinocial [texto apresenta lapso], o Meridiano e o Horizonte) e 4
menores (os Trópicos e os círculos Árctico e Antárctico). Adiante
refere a obliquidade da Eclíptica e como na "esfera oblíqua" este
círculo constitui medida do movimento dos planetas e do orto
(nascimento, Lat. ortus) e ocaso (occasus) das estrelas fixas, sendo os diferentes
ângulos causa da "inequalidad" dos dias e das noites, da mudança dos
tempos e da irregularidade do orto e do ocaso dos Signos.
"Esfera recta" (debaixo da Equinocial, onde esta intersecta perpendicularmente o horizonte) e "esfera oblíqua" (qualquer outra latitude geográfica) são, segundo Olaf Pedersen, termos provavelmente provenientes da utilização dos globos desde a Antiguidade. "Esfera paralela" será a circunstância do observador situado sob um dos pólos. Os "Horizontes" nas esferas recta, oblíqua e paralela (Nicolas Bion, L'usage
des globes celestes et terrestres, et des spheres, suivant les
differens systemes du monde; précedé d'un Traité de cosmographie, 1700)
Segundo Douglas A. Kidd (ed., trans.), Aratus: Phaenomena, Cambridge Classical Texts and Commentaries, Cambridge University Press, 1997, p.348): "It may well have been Eudoxus who introduced these circles into the geometry of the celestial sphere, though the equator and the ecliptic are implied in Plato’s Timaeus myth as the circles of the Same and the Different (36c). All four are described by Autolycus (late fourth century) in his De Sphaera quae mouetur (cf. J.-P. Brunet, AAC* 73-82) and by Euclid in his Phaenomena (cf. P. Chiron, AAC 83—9)". Nos autores "pioneiros", mais antigos, a própria Via Láctea é incluída como um dos "círculos". * AAC: L’astronomie dans I’antiquite classique, Actes du Colloque tenu a l’Universite de Toulouse le Mirail 21-23 octobre 1977 (Paris 1979) Excursus: a Via Láctea Em Grego: γαλαξίας κύκλος, translit. galaxías kúklos, o "círculo leitoso (ou lácteo)". Era um dos onze círculos que os antigos gregos identificavam no céu: o zodíaco, o meridiano, o horizonte, o equador, os trópicos de Capricórnio e Câncer, os círculos Árctico e Antárctico os dois coluros. (Condos, T., Star Myths of the Greeks and Romans..., Phanes Press, 1997, p.110). Em Árabe, é traduzida como al-falak al-labani ou al-da'ira al-labaniyya mas era nessa cultura originalmente chamada al-Madjarra, que parece significar um "sítio ou caminho onde algo era puxado ou arrastado", segundo Paul Kunitzsch. No Próximo Oriente o fenómeno astronómico era associado a palha ou joio. Noutras culturas foi um rio, foi o caminho das almas, etc. Nos Libros del saber... lê-se: "...et llámanla en griego galaxia, et en latin via noctea, que quier dezir la carrera de la noche." (edição Rico y Sinobas, Tomo I, p.43). Também aí se refere o "Caminho de Santiago". Na China Antiga, era thien ho, "o Rio do Céu", "argênteo" (prateado). Aristóletels ensinou que se tratava uma "exalação vaporosa" no ar, um fenómeno que pertencia ao mundo sublunar. Outros, como Demócrito e comentadores como Olimpiodoro acreditavam que era um fenómeno longínquo, na esfera das estrelas. Entre os árabes, encontramos deduções interessantes como as de Ibn al-Haytharn (m. circa 432 AH/ 1041 AD) que considerou, correctamente, que se tratava de fenómeno estelar e distante. Também Al-Biruni, no seu Cânone Masúdico (al-Kãnun al-Mas'udi, c.1030 AD) argumentou que não se observa qualquer interferência quando a Lua e os planetas passam nessas regiões do céu, o que decerto aconteceria se se tratasse de fenómeno sublunar como os aristotélicos defendiam. Acrescentou que "al-madjarra" partilhava das peculiaridades das estrelas (como descritas por Ptolomeu), a saber: encontram-se na mesma esfera e guardam invariavelmente as mesmas distâncias e relações entre si. Resumo: desafios e conseguimentos da abordagem matemática até ao início da Idade Moderna No
passado, foi
necessário harmonizar muitos ciclos diversos e as observações precisas
eram difíceis. Os equipamentos eram rudimentares e no céu não havia uma
grelha desenhada com coordenadas, como vemos nos mapas ou nas apps
de astronomia. O horizonte local era uma referência para os pontos onde
o Sol e Lua tinham os seus ortos e os seu ocasos. Depois, a "esfera
matemática" grega tornou-se a solução mais conveniente, até
"obrigatória",
com os seus
pólos, os seus círculos (a equinocial, os coluros, a eclíptica, os
trópicos...) e suas eventuais intersecções. As estrelas (com a excepção
dos luminares e das "errantes", os planetas) pareciam fixas, nasciam e
desapareciam sempre nos mesmos pontos do horizonte,
e podiam funcionar como um "pano de fundo" ou cenário para o corpos
mais conspícuos. O seu nascimento helíaco (i.e.
primeira visibilidade antes do nascer do Sol) habilitava-as como
marcadores sazonais. Mas os céus, sob escrutínio, revelavam-se repletos
de "inequalidades": tudo
se alterava e era difícil ancorar as medições a"sítios"
concretos: a inclinação da própria eclíptica (onde acontecia o curso
dos planetas e luminares) e até uma "precessão" ou "antecipação"
verificada nos
equinócios, que alterava as longitudes eclípticas das estrelas
supostamente "fixas". Esta era tão lenta que a sua aferição constituiu
um
desafio por muitos séculos: seria homogénea ou variável? Avançava e
recuava, segundo uma (equívoca) "trepidação"? Mas acontecia de facto
qualquer
deslizamento dos equinócios e os séculos acumulados aumentaram o
"problema". O movimento dos "errantes" era ainda mais estranho, com
irregularidades, retrogradações, etc. Bem cedo, nascera na filosofia
grega o princípio da
suposta perfeição dos movimentos circulares, a esfericidade e o
consequente
conceito geométrico de "órbita". Na Mesopotâmia vigorava há muito tempo
um modelo linear e "bidimensional"
agilizado através de séries e interpolações exclusivamente aritméticas,
respaldadas em demoradas e pacientes observações e registos. Nas nas referidas órbitas gregas, a ponderação de elipses ou outras
curvas
"extravagantes" seria filosoficamente pouco sustentável, e assim se
imaginaram epiciclos e deferentes e centros desfasados: pontos imaterias e fictícios, literais "excentricidades". Os
aristotélicos/averroístas estrebucharam durante séculos mas tudo se harmonizava
nessa
desarmonia que multiplicava os expedientes artificiais mas acautelava relativamente bem a
previsão das posições observadas dos
planetas e dos
luminares: "sozein ta phainomena" era o lema. O enfoque era na tradução dos fenómenos, das aparências, e na astrometria. Se estes modelos
repletos de excêntricos, epiciclos e pontos fictícios (como o aequans
de Ptolomeu) eram percebidos numa óptica realista ou apenas
instrumentalista é um debate interessante. As doutrinas filosóficas e
as crenças religiosas e astrológicas "interferiam" nas cogitações
astronómicas. Estabeleciam limites, sugeriam ciclos cronológicos amplos e divinamente inspirados,
postulavam uma "geometria sagrada". O contexto intelectual
não permitia ponderar seriamente alternativas geométricas ou
ponderações cosmológicas alternativas, apesar de um ou outro
precedente. Mas uma Terra pesada e inamovível parecia evidente, e não
se observava paralaxe evidente nas "estrelas fixas", o que aconteceria
se a Terra rodasse em torno do Sol (um dos "problemas" apontados ao novo
sistema de Copernicus). Ainda não se concebiam as enormes
proporções que o Universo depois assumirá.
Deixemo-nos guiar pelas aparências e imaginemos que o nosso planeta é rodeado por uma abóbada esférica que gira à nossa volta, de Leste para Oeste, no intervalo de um dia, tendo como eixo de rotação uma recta imaginária que é o prolongamento do eixo do nosso planeta. As estrelas não estão espalhadas pelo céu, antes equidistantes e fixadas nessa esfera. Em
comparação com a Esfera Celeste, a dimensão da Terra é considerada
diminuta, como um ponto. Por isso, as constelações mantêm os seus
padrões mesmo quando observadas de regiões do planeta muito distantes
entre si. Toda
a astronomia até ao final do séc. XVI se baseava na observação a olho
nu, facto muitas vezes subestimado. As dificuldades na observação e na
obtenção de resultados precisos teria de ser compensada com empenho,
observações assíduas e prática na estimativa da amplitude das mudanças
das posições dos corpos celestes e
o acesso a observações similares registadas ao longo de um período tão
extenso quanto possível. Estas seriam condições determinantes para a
obtenção de resultados significativos.
Tempo e persistência. Recorreu-se à sombra do gnómon ("ponteiro"), o mais simples
dos instrumentos (um apontador vertical sobre uma base), mais tarde
globos com
os círculos principais da esfera, um
qualquer instrumento de pontaria para efectuar, entre outras, medições
de alturas. Não é improvável que nas medições angulares se recorresse,
a princípio, às mãos e dedos com o braço estendido, bem como à sombra de uma pessoa. Depois, a soluções
igualmente simples mas mais engenhosas, do antigo merkhet
Egípcio com o seu prumo aos quadrantes, armilas e balestilhas
utilizados até há alguns séculos. E tudo isto naturalmente num contexto
geocêntrico, o dos fenómenos ou aparências, com a Terra estacionária e
o céu numa regular rotação diurna. Depois temos outros ritmos
relacionados com os luminares, o Sol e a Lua, que definem os padrões
fundamentais e as medidas do tempo: o dia, o mês, o ano das estações...
são as regularidades fundamentais.
Todas
as estrelas partilham um movimento contínuo e uniforme na direcção
este-oeste; enquanto algumas percorrem órbitas amplas e estão visíveis
durante grande parte da noite antes de mergulharem no horizonte oeste,
outras fazem um percurso menor e estão visíveis menos tempo. Outras,
entretanto, estão sempre visíveis, circulando em torno do pólo. Por
fim, estrelas diferentes estão proeminentes em diferentes épocas do
ano, voltando ao mesmo sítio em anos sucessivos.
Os nascimentos e ocasos observáveis das estrelas podem ser assim definidos (D. R. Dicks, Early Greek Astronomy to Aristotle, Cornell University Press, 1970. p.13 [trad. nossa]): - Nascimento helíaco ou heliacal (nascimento matinal observável): primeira visibilidade no horizonte leste antes do nascer do Sol. A estrela está suficientemente avançada em relação ao Sol para se poder observar e, em dias sucessivos, o seu período de visibilidade aumenta. - Nascimento acrónico (Lat. ortus vespertinus, o nascimento vespertino observável): última visibilidade da estrela que nasce logo após o pôr-do-Sol. Em noites sucessivas, a estrela nasce no horizonte leste enquanto ainda há demasiado brilho solar; torna-se observável apenas mais tarde durante a noite. - Ocaso cósmico (ocaso matinal observável): a primeira vez em que observamos a estrela no poente mesmo antes do nascer do Sol. Nas noites anteriores, a estrela ainda não alcançou o horizonte oeste antes do nascer do Sol; está observável durante a noite. - Ocaso helíaco (ocaso vespertino observável): último ocaso observável antes do nascer do Sol. Nas noites sequentes, a estrela terá chegado ao horizonte oeste enquanto ainda há demasiado brilho solar. Estrela estará acima do horizonte durante o dia. No
intervalo entre o ocaso helíaco (ou heliacal) e o sequente nascimento
helíaco, a estrela permanece invisível durante a noite. Ao longo de
outros períodos, a estrela pode estar observável dependendo da época do
ano, da sua posição em relação ao Sol e da latitude do observador (do
seu horizonte particular). A chamada Precessão dos Equinócios (fenómeno descoberto por Hiparco [Hipparkhos, c.190-c.120 a.C.]) determina que, ao
longo dos séculos, as estrelas observáveis numa determinada época do
ano se alterem. É o deslizar gradual do ponto Vernal através das constelações ou o inverso, se preferirmos a perspectiva medieval.
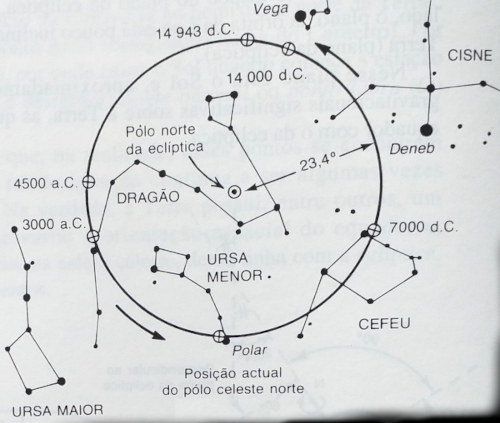 Efeitos da Precessão e "percurso" do pólo norte celeste, descartando o muito menor efeito de nutação (causado por alterações cíclicas na órbita lunar, que faz com que a orientação do eixo da Terra tenha um percurso legeiramente oscilante, não exactamente circular). O ciclo precessional demora cerca de 25800 anos. Há quase 5000 anos, para os construtores Egípcios do Império Antigo, o pólo estava próximo da estrela que conhecemos como Thuban (α Draconis na designação de Bayer). A arqueologia encontra vestígios na orientação de detalhes arquitectónicos em estruturas dessa época recuada, atendendo à importância simbólica atribuída a essa região pivotal do céu e às estrelas "que não pereciam" (i.e. circumpolares). Esquema recolhido da excelente Introdução à Astronomia e às Observações Astronómicas (2ª ed.) de Máximo Ferreira e Guilherme de Almeida (Plátano, Edições Técnicas, 1995, p.132)
Já Lucano (Marcus Annaeus Lucanus, séc. I AD), no poema épico "Farsália" (Pharsalia ou De Bello Civili,
lib. III) mencionava a navegação pelas estrelas (tendo anteriormente avisado que não se
utiliza o Zodíaco pois este não é fixo, i.e. nasce e põe-se, "enganando os
pobres marinheiros"): Há quinhentos anos, aquando da nossa expansão marítima, a estrela Polar estava afastada do pólo cerca de 3.5º, daí a necessidade do "regimento" (chamado "do Norte" ou "da Polar"), conjunto de regras que permitia, em função da posição da estrela no círculo diurno, aplicar uma correcção e determinar o norte verdadeiro em função da configuração dessa "estrela do norte" com as que estavam nas imediações). Hoje, Polaris está apenas a cerca de 1º do pólo e o valor da sua elevação (medida com um qualquer instrumento de alturas) permite conhecer a latitude geográfica (a que os nossos marítimos chamavam ladeza) quase de imediato com razoável aproximação.
Distância polar da estrela α Ursae Minoris (Polaris) nos anos centenares relevantes para o nosso tema: Segundo
Fontoura da Costa, os marinheiros portugueses dos séculos XV ao XVII
usaram duas qualidades de instrumentos náutico-astronómicos: os que
forneciam directamente a altura angular do astro observado (como o
astrolábio, o quadrante, etc.), e os que davam a altura mediante a
relação de dois elementos lineares (como a balestilha e as tavoletas ou
tábuas da !ndia [com as quais os portugueses tomaram contacto quando
chegaram ao Índico]). (A Marinharia dos Descobrimentos, Lisboa: Agência Geral das Colónias, 1939, p.18)
Figura humana representada no pólo norte da Esfera Celeste no Reportório dos Tempos de Valentim Fernandes (edição de 1528), nomeando os rumos principais: cabeça (norte), ombro esquerdo, braço esquerdo, etc. [Considerou-se, desde cedo entre nós, a figura humana voltada para o observador.] Gravura indicava as alturas da Polar
em Lisboa, quando a guarda dianteira da Ursa Menor (formada pelas estrelas β e γ da posterior notação de Bayer) chegava ao
correspondente rumo [N.B.: nesta figura somente estão correctos os valores respeitantes aos rumos N (cabeça), SE (abaixo do braço esquerdo) e S (pé), v. Luís de Albuquerque , Navegação Astronómica, Comissão Nacional para as Comemorações dos Descobrimentos Portugueses, Lisboa: 1988, p.25]; à direita: roda com regimento da Estrela do Norte
segundo o Livro de Marinharia de João de Lisboa. A prioridade na utilização
da Ursa Menor na navegação era atribuída, desde a Antiguidade, aos Fenícios ("Phoenices primi, famae si creditur...").
Saliente-se que só algumas das regras (posicionais) se poderiam usar em
cada noite, e as regras utilizáveis variavam obviamente com a época do ano. O
historiador Gabriel Ferrand defendeu que a indicação da altura da Polar
em isba (polegadas) para a
determinação da latitude de um porto era, sem dúvida, uma prática
antiga no Oceano Índico (Introduction à l'Astronomie Nautique Arabe,
Paris: Paul Geuthner, 1928, p.155 et seq.).
Aí se praticaria principalmente uma navegação por alturas iguais,
leste-oeste e vice-versa. Também usada no Atlântico, esta técnica teria
em conta a posição das guardas da Ursa Menor caso utilizasse a estrela Polar (e
recorreu alternativamente a outras estrelas conhecidas).
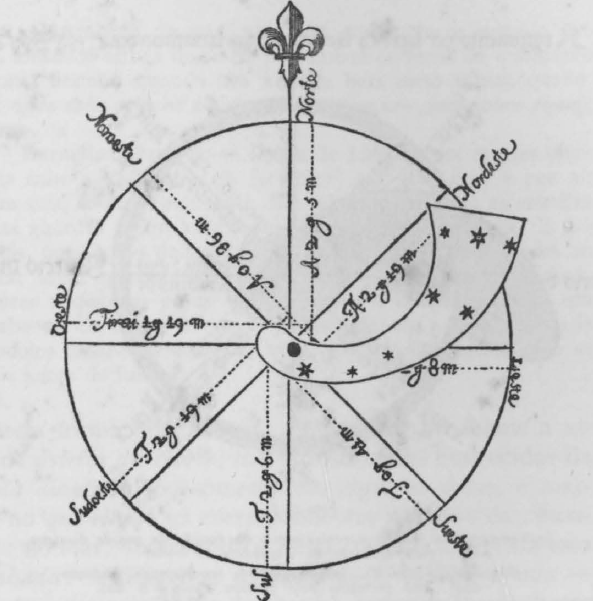 Instrumento rotativo com a figura da Buzina ou Bozina para facilitar a leitura (Regimento do Norte, por Luís Serrão Pimentel). Usava-se a estrela a que se chamava Major Frater (β, Kochab) ou os Dos Frares ("dois irmãos"). A guarda dianteira era a estrela β, a guarda traseira era a estrela γ, a terceira guarda a estrela 5 (ulterior designação de Flamsteed)
Quando as guardas, a chamada "Boca da Bozina" (i.e. estrelas β, γ e 5 UMi) não estivessem observáveis, ou como complemento, recorria-se a outras estrelas. As nossas fontes destacam duas: João de Lisboa (c.1470–1525) referiu uma estrela a que chamavam "Meca" no Tratado da Agulha de Marear. Segundo o Professor Luís de Albuquerque (Navegação Astronómica, Lisboa: Comissão Nacional para as Comemorações dos Descobrimentos Portugueses, 1988, pp.39-40), esta seria a estrela γ (Gamma) Cephei. O texto original é confuso mas Albuquerque clarifica-o: quando as guardas estão na linha leste-oeste (ou a guarda dianteira, i.e. a estrela β, Kochab, na linha abaixo do leste [Albuquerque refere "oeste" mas deve ser um lapso]), a "Meca" (ou novena) e a estrela Polar estão em linha com o pólo, e a diferença (ângulo horário) entre as linhas pólo-Meca e pólo-Kochab seria de 9 horas (=135º; 1 hora equiv. 15º). 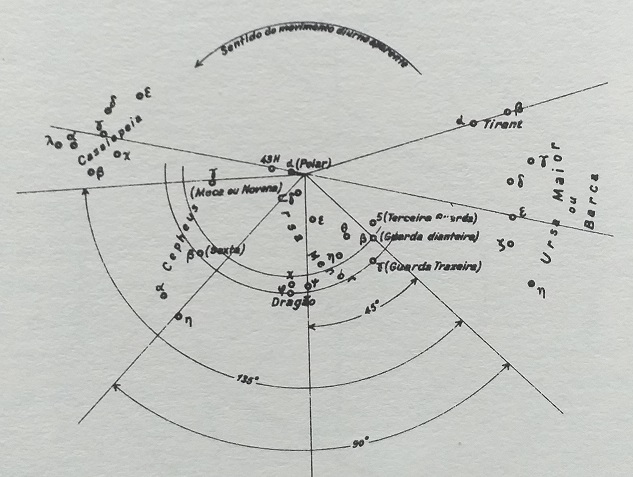 As estrelas setentrionais referidas em textos náuticos portugueses do séc. XVI (Luís de Albuquerque, Navegação Astronómica, Op. cit., 1988, Fig. 10) Também surge, num Regimento da declinação do sol e no conhecido atlas de Lázaro Luiz, uma "regra do Norte" que, segundo Fontoura da Costa (A Marinharia dos Descobrimentos, Lisboa, 1939, p.57), não se encontra em documentos anteriores. Segundo o atlas de 1663 do mencionado cartógrafo: "Ha hua estrela muito chegada ha ho norte a qual tem esta fegura [v. ilustração seguinte] quamdo vai a seu lugar tomase haa altura a ela quãdo as guardas vão abaixo da linha de noroeste hora & mea, & ela vai ao braso de leste [a] altura que tomardes ne[s]sa estais & quammdo as guardas vão hua hora & mea esta o gião no braso do este da altura que então tomardes nesa estareis, por q[ue] não a tirar nem meter por Rezaon destar ho norte no e[i]xo e ho giaom esta neste does lugares taõ alto como o norte"  Posições da estrela Gião segundo Lázaro Luiz (in: Fontoura da Costa, op. cit., Fig. 32) Fontoura da Costa confessa não possuir elementos para a identificação dessa estrela "Gião" (questionando se o nome se relacionaria com "Julião" ou "Guião"). Luís de Albuquerque (op. cit., p.41) confirma que seria "Guião", nome grafado numa anotação marginal na folha do atlas. Acrescenta que é possível interpretar o texto e identificar assertivamente esta estrela como a "43 H" (seguindo uma antiga classificação de J. Hevelius) em Cepheus (historiador utilizou o já antigo atlas celeste de Richard Schurig: Tabulae caelestes continentes omnia stellas coeli..., 2ª ed., Leipzig, 1909). De facto, a única estrela "chegada ao Norte" que responde às condições descritas, ficando "...tão alto como o Norte" é a ulteriormente catalogada como SAO 181 (HD 5848; TYC 4623 1236), em Cepheus, cuja magnitude equivale a 4.2. Está, de facto, próxima (~3 graus) da Polar (α UMi na notação de Bayer) e seria observável num céu razoável. Que o teria sido, prova-o o esquema que acima se disponibilizou do intrumento rotativo de Serrão Pimentel, pois desenha a figura da constelação incluíndo claramente a estrela 5 UMi (SAO 8024), de magnitude equivalente, nas guardas. Se esta se observava, também a outra o seria. Em resumo, nas duas posições das guardas postuladas na regra, a estrela gião ficaria numa mesma linha de alturas com α UMi, à direita e à esquerda desta (respectivamente) na perspectiva do observador voltado para Norte. Neste sentido, o texto constituía, na realidade, um regimento para esta estrela particular, enquanto "marcador" da altura correcta, permitindo a medição imediata da elevação do pólo. Contudo, o método seria somente complementar e válido, quando exequível, apenas em dois momentos da rotação diurna (referimo-nos ao dia natural, de 24 horas) da Bozina. 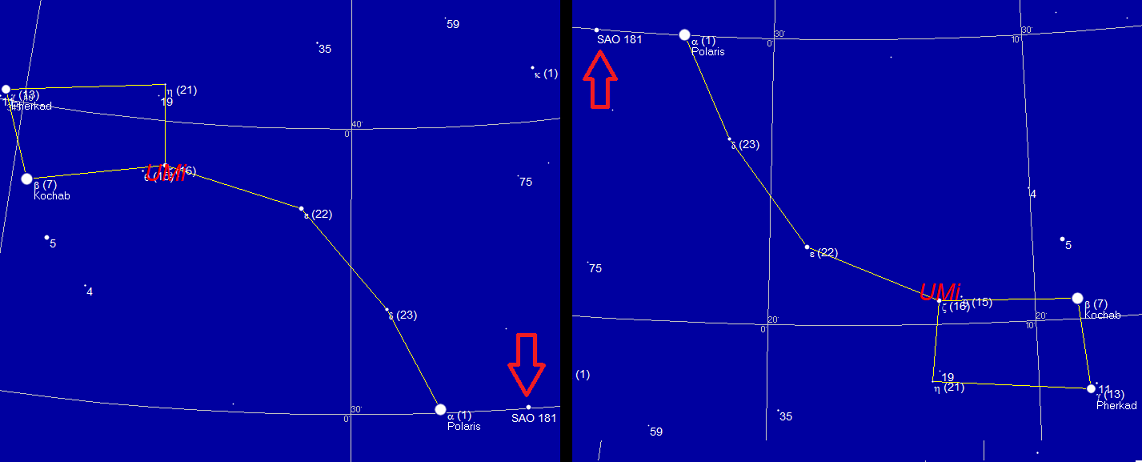 Simulação recorrendo ao programa SkyMap Pro para a epoch 1550 AD. A estrela "Gião" surge indicada pela seta.
Entretanto, coligem-se outras de estrelas, com indicações (regras) para com a sua ajuda determinar a latitude (boreal ou austral). Os nomes não estavam normalizados e podiam ser, por exemplo: "a mais austral do Rabo da Baleia", "Alveida ou Testa de Aries", "Cabra no Hombro de Carreteiro", "a do meio dos Três Reis Magos", "Canopo ou Leme da Nau", "a menos boreal do Leme da Barca", "a Lúcida da Lira", etc. As seis estrelas designadas numa precoce relação de João de Lisboa eram: "Azeviche" ou "Spica", "Vega", "Denebagide", "Ras Delauege", "Altir" e "Calbalatear". Posteriormente reconheceu-se a vantagem da utilização da altura meridiana do Sol (respaldada na informação astronómica, i.e. a altura do Sol para determinada ladeza (latitude) ao longo dos dias do ano, registada nos conhecidos regimentos do norte e do Sol). Utilização da declinação do Sol ao meio-dia, ou altura do pólo ao meio-dia, medindo (com o chamado astrolábio náutico ou com o quadrante) a altura do astro no ponto culminante ("pesar o sol"). Tratava-se da determinação da latitude a partir da maior altura do Sol, desde que conhecida a declinação do astro na data da observação. O método já se encontrava no De Compositione et Utilitate Astrolabii, do pseudo-Messahalla, todavia somente para latitudes a norte do Trópico de Câncer. Muitos outros astrólogos árabes e judeus medievais se ocuparam do problema. (Luís Albuquerque, Estudos de História, vol. III, col. "Acta Universitatis Conimbrigensis", Universidade de Coimbra, 1975, p.117 et seq.). Podemos a seguir ler um resumo das regras (casos gerais) da declinação do Sol a partir da "versão condensada" por Duarte Pacheco Pereira (Luís Albuquerque, Estudos de História, vol. III, Op. cit., p.135). φ designa a latitude do lugar, δ a declinação do Sol e h a sua altura meridiana:  No clássico Admiral of the Ocean Sea (Boston, Little Brown and Company, 1942), Samuel Eliot Morison refere como Cristóvão (Cristoforo) Colombo se enganou um par de vezes na aferição da latitude pela Polar durante a sua primeira viagem. Pior, tudo indica que se enganou na estrela cuja altura devia medir. Não se tratava de um desvio da agulha de marear pois o próprio Colombo é um pioneiro no registo desse problema e escreve a 30 de setembro de 1492: "las agujas noroestean una cuarta [de hora]". Era o incompreendido problema da declinação magnética (o "ferro de norte a sul", que era "cevado" na "pedra de cevar", i.e. magnetita), como refere João de Lisboa, desviava-se da sua direcção (o seu nordestear e noroestear); tampouco se tratou de uma questão de longitude (a "altura de leste-oeste" ou "longura" dos nossos marinheiros de outrora; a sua imprecisa determinação estava sujeita à estima, com carta e métodos expeditos que se baseavam na experiência dos capitães e pilotos, sem relógios ou cronómetros antes do primeiro protótipo fiável criado pelo Inglês John Harrison somente no século XVIII. (v. Fontoura da Costa, A Ciência Náutica Portuguesa Na Época Dos Descobrimentos, Comissão Executiva das Comemorações do Quinto Centenário da Morte do Infante D. Henrique, 1958, p.72). Despertou muito interesse, em Portugal e no estrangeiro, um "engenhoso" método pela variação da agulha (i.e. declinação magnética somada ao desvio). João de Lisboa, por exemplo, afirmava pela experiência que tal seria possível a partir do "meridiano vero" (que passava entre algumas ilhas dos Açores e em Cabo Verde), onde a agulha apontaria exactamente o norte geográfico, sendo possível pela variação proporcional da agulha conhecer a "altura de leste-oeste" em léguas. Tratava-se de um equívoco e essa determinação era obviamente impossível. D. João de Castro verificou na prática a inutilidade do método pois "as variações que fazem as agulhas não é por diferenças de meridianos" (Roteiro de Lisboa a Goa, 1538). Mas o "mito" continuou e até Mercator se debruçou acerca do tema. Na sequência desta ponderação, é a Cristóvão Bruno (Borro, Borri ou Burro) que se deve o primeiro esboço de uma carta de isogónicas (primeiro quartel do século XVII). Entretanto, foi possível (em algumas circunstâncias) aproveitar o conhecimento de regiões de linhas isogónicas, onde se sabia que a agulha era fiável, formando faixas regularmente estreitas na direcção aproximada norte-sul. Não sabemos se a opinião do biógrafo de Colombo, que lemos um pouco acima, é a mais plausível. Em caso afirmativo demonstra uma dificuldade inesperada na observação concreta, sempre uma possibilidade quando as condições não são as ideais (horizonte obstruído, nuvens...), relacionada com a latitude, o que é algo inesperado. Segundo Morison, em Moustique Bay (Haiti), Colombo mediu a altura da estrela "Er Rai" (ou Errai, Gamma Cephei), supondo ser a Polar (Op. cit., p.284). No local que se chamará Puerto Gibara (21° 06' N) quase duplicou a latitude determinada (obtendo 42° N), o que o próprio considerou estranho. Morison descreve diversas interpretações e propõe que se tratou de uma confusão entre a Estrela Polar e Alfirk, em Cepheus: "The reasons for this colossal error have much exercised the pundits. Navarrete postulated an imaginary, nonexistent quadrant that read double. Magnaghi argued that Columbus was trying to throw the Portuguese and others off the scent. Las Casas believed that the scribe copied “21” as “42.”The real explanation is simple: Columbus picked the wrong star. He was “shooting” Alfirk (β Cephei), which in November bore due north at dusk; mistaking her for Polaris, whose familiar “pointers” were below the horizon. Columbus knew perfectly well that latitude 42° N was fantastically wrong. He had earlier noted in the Journal that Guanaham was on the same parallel as the Canaries; and in his printed Letter on the First Voyage he gives the mean latitude of his new discoveries as 26° N. But, as he remarked rather plaintively in his Journal, “The North Star” (that is, Alfirk) “looks as high as in Castile.” (pp.258-59) Também as conjunções, as distâncias lunares e os eclipses eram muito conhecidos pelos meados do século XVI, mas mantinham-se sem utilidade prática, especialmente por falta de instrumentos e de tábuas. (ibid., p. 68). O tradicional método de alturas-distância implicava uma avaliação da extensão do grau do meridiano. Já vimos que os pilotos Portugueses mediam a altura meridiana do Sol e deduziam a latitude com a ajuda das tabelas da declinação do luminar (conferindo com o valor para a data concreta no calendário). Era particularmente importante quando se atravessava a equinocial e se deixava de ver a "Estrela do Norte". Quanto à interpretação do "novo" céu austral, o veneziano Cadamosto (1432-1488) acreditava que este manifestaria, de algum modo, por simetria, a presença de um "carro" (espelhando a Ursa Maior boreal, conhecida popularmente como "barca", "carro" ou "carro de David") e de uma hipotética "Estrela do Sul" assinalando o pólo. Esta perspectiva enquadrava-se na mundividência coeva. Entretanto, Vespúcio (Amerigo Vespucci, nascido em Florença em 1454), durante as suas viagens ao sul, associou as estrelas da Cruz (o Cruzeiro do Sul, pela primeira vez descrito como constelação na famosa carta de Mestre João Faras, enviada das Terras de Vera-Cruz a D. Manuel em 1500) às quatro "estrelas brilhantes" (simbolizando as quatro virtudes cardeais) descritas por Dante Alighieri nos céus que o poeta avistou quando voltou à superfície após percorrer as cavernosas regiões infernais.  O
nocturlábio permitia determinar a hora durante a noite. Num disco
rotativo interior seleccionava-se a estrela de referência e alinhava-se
esta com a data específicano disco exterior. Apontava-se a estrela escolhida
(muitas vezes Kochab, na Ursa
Menor) a partir do centro do instrumento com o ponteiro. A intersecção
deste braço com um limbo graduado em horas indicava a hora eque se queria determinar.
Utilização do nocturlábio, Manuel de Navigation, Jacques de Vaulx, Le Havre, 1583 (BnF, département des Manuscrits, Français 150, f. 17)
A Longitude no Mar Tratava-se de um problema muito complexo, essencial para (em conjunto com a latitude) encontrar precisamente o "ponto no mar", sem ser por estimativa. Na realidade não existia qualquer método. Duarte Pacheco escrevia, em 1505, no seu Esmeraldo de Situ Orbis (cap. 8): "...os graaos da longura se contam de ouriente em oucidente a que os marinheiros chamom lest e oest & por ser difícil podem se saber por nom terem ponto firme & fixo [origem fixa] como som os pollos que unem ha ladeza nom curo de nisto mais fallar." Em mar aberto, estimava-se o percurso efectuado (rumo-distância) avaliando a velocidade do vaso e com a ajuda das cartas, da agulha e da ampulheta. Também, obviamente, a observação de qualquer ponto de referência (quando disponível). A experiência do piloto ou capitão era importante. Depois usaram-se cordas que se estendiam, com nós regularmente espaçados (com uma prancha flutuante numa extremidade) e a ampulheta para calcular a velocidade num determinado intervalo de tempo (v. ilustração seguinte). Era o chamado método da "barquinha". Mas eram sempre métodos expeditos e imprecisos. Em resumo, a chamada fantasia ou estimativa (da velocidade do vaso e medindo o tempo) foi durante séculos o único processo de que o piloto dispunha para avaliar a distância navegada. A barquinha é de uso mais recente, disseminando-se apenas no séc. XVII. Entre nós, usou-se como referência da "longura" o meridiano a passar pelo Cabo de S. Vicente (que era considerado também o de Lisboa). A medição do tempo era muito imprecisa. O tempo a bordo era indicado por relógios de areia, de meia hora. Um relógio de sol só poderia ser usado na elevação do pólo (latitude) para a qual havia sido construído, ou devolveria resultados errados. Mas, segundo Fontoura da Costa, havia os "universais" com um prato horizontal com uma pequena agulha magnética (para poderem funcionar paralelamente ao horizonte) e um disco das horas móvel, para poder ficar paralelo ao equador na latitude em que se empregavam. (A Marinharia dos Descobrimentos, p.376). Os relógios de areia eram preferidos e continuaram a ser utilizados até ao séc. XVIII. Quanto à sua (im)precisão, citamos Simão d'Oliveira: "Em 2 ou 3 dias passante de quarto de hora a que segundo este modo respondem 3 graos e 45 minutos..." (Arte de Navegar, Lisboa: Pedro Crasbeeck, 1606, p.145). Entretanto, diversas estratégias foram surgindo para obviar este problema. A observação dos eclipses (que em longitudes diferentes se observam em simultâneo mas a horas locais diferentes) era complicada. São fenómenos que apenas acontecem esporadicamente e mesmo em terra é difícil determinar o seu ponto médio. Galileu advogou a utilização dos movimentos dos satélites de Júpiter (que, apesar das dificuldades, James Bradley [1692-1762] tentará utilizar). Sem cronómetros, a ideia mais prometedora foi, sem dúvida, a da utilização da Lua, com a sua rápida progressão diária (quase 13.2°, i.e. 1/27 da circunferência do céu). Mas para isso, precisavam estar reunidas várias condições: instrumentos precisos para medir o ângulo entre a Lua e uma estrela de referência escolhida, um catálogo estelar rigoroso e tabelas precisas dos movimentos da Lua. Demasiado difícil combinar estas exigências e observar a bordo de um navio, pois seria necessário apontar ambos os corpos (a Lua e uma estrela) simultameamente com o bastão. Demais, um erro de alguns minutos na medida do ângulo no céu produziria um erro 27 vezes maior na longitude terrestre do local de observação deduzido. Sabia-se bem que um relógio seria muito mais eficiente. O de pêndulo fora inventado por Christian Huygens em 1656 (descrito na obra Horologium Oscillatorium). A partir daí, diversas tentativas foram patrocinadas, ao mais alto nível, para produzir cronómetros adequados à utilização no mar (um ambiente extremamente exigente: temperatura, pressão, humidade, movimento). Se um cronómetro de bordo errasse um minuto, o diferencial em longitude seria de apenas 1/4º (pois 1º = 4 minutos de tempo). Mas o desafio náutico era muito complexo devido, por exemplo, à aceleração provocada pela temperatura e pela dilatação dos metais, cujos coeficientes foram, obrigatoriamente, tidos em consideração pelos melhores relojoeiros (e.g., Harrison, Lapaute, Berthoud). John Harrison (1693-1776) foi quem resolveu directamente o problema para o Almirantado Inglês, criando relógios que foram ulteriormente testados e adoptados. O seu protótipo "H4" foi testado com sucesso numa viagem a Barbados, nas Antilhas. O método baseava-se na diferença de tempo (da qual se deduzia facilmente a longitude) relativamente à hora concomitante de um meridiano de referência, seguindo uma teoria muito simples já antes avançada pelo astrónomo, cartógrafo e construtor de instrumentos Gemma Frisius (1508-1555). De facto, a única resposta satisfatória foi o cronómetro, como será mais tarde o telégrafo eléctrico em terra. Como consequência, o cronómetro exigiu tabelas e instrumentos mais precisos, bem como um melhor controlo do tempo e da marcha dos relógios. Nos séculos XVII e XVIII, Paris era o "ponto zero", aí passando o meridiano de referência (a Revolução Francesa promove-o, a par da adopção do sistema métrico e da efémera imposição do Calendário Republicano). Entretanto, reflectindo a hegemonia britânica e a relevância do Observatório de Greenwich, a referência internacional passará (1884) a ser o meridiano dessa prestigiada instituição. 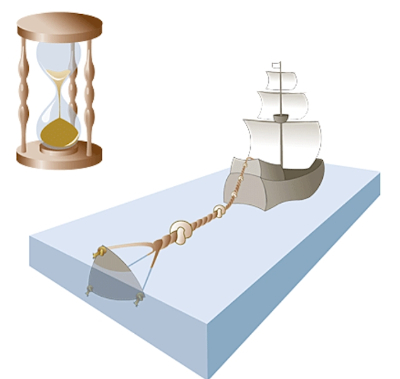 Determinação da velocidade no séc. XVII (fonte: oceanservice.noaa.gov).
Na navegação actual, 1 minuto de latitude equivale (aproximadamente) a
uma unidade chamada "milha náutica", 1.852 km. Uma
velocidade de 1 milha náutica por hora é 1 nó (Ing. "knot", abrev. kn;
kt é mais usado em em aviação)
A Esfera
Celeste
Trata-se de uma estrutura conveniente: "Observers reckoning themselves situated on the earth gazing outward to an infinitely large enclosing dome capture their situation more readily and naturally. Indeed, even today those who use astronomy for practical means (such as navigation, surveying, orienteering, and so on) routinely use this perspective. A further advantage of such a conception is that it can capture directions and relative positions of celestial bodies, without the need to consider their distances from the earth." (Clemency Montelle, Chasing Shadows: Mathematics, Astronomy, and the Early History of Eclipse Reckoning, The Johns Hopkins University Press, 2011, p.22) O Universo ”geocêntrico”, o das aparências que observamos, foi historicamente representado através da ordem e harmonia dos movimentos circulares. As estrelas consideravam-se “fixas”, equidistantes do centro (ocupado pela Terra) e plasmadas numa gigantesca estrutura esférica. A observação continuada permitiu compreender as sucessivas posições do Sol em relação ao fundo de estrelas. "La espera del ochauo cielo ["A esfera do oitavo céu", das chamadas "estrelas fixas"] es la primera en que a estrellas figuradas, et es la mas noble de todas las otras siete, de que fablaremos adelantre. porque está mas cerca del noueno. Et la uertud que del rescibe. esta la parte por las otras, cada una según que ell a menester, et á él conuiene. Esta espera es toda llena de estrellas ya grandes, et menores, et medianas. Et figurada de todas las figuras que fueron, et son. et seer podrán, et en cada una dellas a su uertud sigund la de Dios puso en aquella espera donde ellas son. Et por esso queremos fablar dellas. Et cuemo quier que las de los signos sean mas nobles en uertud. et mas connoscidas que las otras, et mas connoscidas de los omes. Otrossí porque el sol cosre por aquella carrera por do los signos son. que es la mayor et mas noble et de mayor uertud que todas las otras estrellas. Et otrossí porque las otras planetas fazen su curso por aquel mismo logar, et dally an la mayor uertud. por esso semesíaba razón que daquellos signos fablássemos primero." (Libros del Saber de Astronomía del Rey D. Alfonso X de Castilla, ed. M. Rico y Sinobas, Madrid, Tipografía de Don Eusebio Aguado, 1863; Tomo I, p.11). Nessa conceptualização os céus podem ser inscritos em dois círculos máximos (i.e. que dividem a esfera em duas metades): a Eclíptica que é o caminho que o Sol percorre e o Equador (Equinocial, gr. "isemerinos"), a meio caminho dos pólos, os dois pontos imóveis, invariáveis, da esfera. Estes dois círculos intersectam-se num ângulo de 23,5 graus, aproximadamente. Ptolomeu (AD 138) indicou o valor de 23º51’, Regiomontanus (em 1490) registou 23º33’ e Tycho Brahe (em 1592) 23º31’. Era difícil calcular com precisão devido às limitações da instrumentação mas desde a Antiguidade que se sabe que este valor vai decrescendo. O Zodíaco é uma faixa (convencionalmente com 12 graus de latitude, algumas fontes outorgavam-lhe outra espessura) que se estende 6 graus para norte e 6 graus para sul da Eclíptica (definindo assim aproximadamente o espaço até onde se observam as deambulações dos planetas e da Lua. sendo as mais amplas as da Lua e Vénus). "(...) the heavens may be inscribed with two ‘great circles’ (circles dividing a sphere into equal halves). One defines the path along which the sun appears to travel, the ecliptic, and the other lies at the midpoint between the two still points of the heaven, the celestial equator." (J. C. Eade, The Forgotten Sky..., Oxford, Clarendon Press, 1984, p.4). A informação posicional de um corpo celeste é, tradicionalmente, referida a um dos dois círculos referidos: a Eclíptica ou o Equador Celeste. Historicamente, as coordenadas eclípticas foram privilegiadas. A distância ao longo da eclíptica, medida em graus de Longitude (celeste), era tradicionalmente contada por signos, cada um com 30°. [A Latitude (celeste) constitui a segunda coordenada, perpendicular ao mesmo círculo, dito oblíquo. A do Sol é, por definição, nula: é justamente o seu percurso aparente que desenha ou define a Eclíptica; a dos planetas é variável.] Assim, a longitude de um corpo não seria indicada como 70°, mas como Gemini 10, sendo Gemini o segundo signo zodiacal. Por outro lado, a medição que se respalda no Equador Celeste, hoje prevalecente, é contada em graus de Ascensão Recta ao longo desse círculo (exprime-se geralmente em tempo, i.e. horas e minutos: 1º=4min.; 15°=1h) e em graus de Declinação (na perpendicular ao mesmo círculo de referência). O ponto de origem de ambos os sistemas de coordenadas é conhecido como Primeiro Ponto de Aries, um dos dois pontos de intersecção dos dois círculos máximos referidos, e o que marca o início da Primavera no Hemisfério Norte. [Pela sua posição privilegiada, o signo Aries era conhecido como Primus Aries - Signorum princeps - astrorum dux ou ductor gregis principium (Firmicus, Mathesis, II,10; ed. Kroll)].
Os movimentos dos planetas clássicos, respectivamente: períodos siderais (revoluções), movimentos diários médios (incl. máx. para os mais velozes; N.B. "movimento médio" é o intermédio entre o mais lento e o mais rápido) e amplitudes máximas em latitude (norte e sul) a partir da Eclíptica. Valores arredondados, coligidos por J. C. Eade (The Forgotten Sky, 1984, pp.22-23)
Como J. P. Goold explica na introdução à sua edição do tratado de Manilius (Astronomica. Loeb Classical Library 469. Cambridge, Harvard University Press, 1977), é sabido que as constelações ao longo da Eclíptica se foram desenvolvendo antes do aparecimento do conceito de um zodíaco normalizado, duodecimal. Segundo Hiparco, Eudoxus terá colocado o Ponto Vernal no 15º grau de Aries. Aratus colocou-o no início dessa constelação. Todavia, a diferença entre as datas destes autores determina que a diferença precessional seja de somente 1 grau, aproximadamente. A referência ao 8º grau pode recuar, como Neugebauer sugeriu, ao chamado "System B" da teoria lunar Babilónica. Este valor deve ter estado próximo da realidade sideral quando o sistema zodiacal foi implementado. A opção do 8º grau foi geralmente adoptada pelos autores Romanos, e.g., Vitruvius, Columella ou Plinius, autor na Naturalis Historia). Martianus Capella foi um dos principais responsáveis pela sua disseminação medieval. A "solução" astrológica surge no Tetrabiblos I.22 (ed. Robbins), com a afirmação da estrutura do 'zodíaco tropical' (desligado dos sidéreos, das estrelas reais): o início de Aries é o Ponto Vernal e se este se move, todo o Zodíaco se move com ele. É, no fundo, um "zodíaco artificial". O Zodíaco que utilizamos é Tropical (ancorado nos equinócios e solstícios). Todavia, alguns séculos após Ptolomeu (que o advogou), o Zodíaco Sideral (baseado nas estrelas, nas constelações) continuava a ser privilegiado. Houve uma época (até cerca de 2100 a.C.) na qual, devido ao fenómeno da Precessão dos Equinócios, o Equinócio Vernal se situava (na antiga sequência de asterismos e constelações criada na Mesopotâmia) na constelação do Touro de Anu, ou Touro do Céu (mul GU4.AN.NA) e o nascimento das Plêiades (mul MUL ou zappu) assinalava a abertura da estação vernal, primaveril. Por esta razão, estas surgem à cabeça nas listas Babilónicas dos asterismos e constelações no "Caminho da Lua", enquanto a última constelação nessa sequência era mul LU,HUNG.GA (mais tarde substituída no zodíaco Grego por Aries), Hoje, tendo atravessado as estrelas de Aries, o Ponto Vernal situa-se, sideralmente, nas estrelas da constelação Pisces (não confundir com o signo no zodíaco Tropical, entretanto desfasado da constelação que lhe atribuiu o nome). - Precessão dos Equinócios: já mencionada nesta página, trata-se da oscilação do eixo da Terra, semelhante à de um pião sobre o seu eixo. Determina que os pólos equatoriais descrevam um círculo em torno dos pólos da Eclíptica em cerca de 25800 anos, equivalendo a um deslocamento de 1º em 72 anos. Assiste-se, pois, a um deslocamento aparente das estrelas da direcção Leste, de modo a que a sua longitude aumenta lenta e gradualmente.
Quando se aborda o quadro de referência científico entretanto adoptado pelos gregos, deparamo-nos, historicamente, com o problema das convenções utilizadas para o início dos signos, fundamental quando se utiliza um sistema de coordenadas (e o mais antigo é justamente o eclíptico). E como saber se os autores se referiam a "signos" ou às constelações aparentes, as estrelas observadas? O zodíaco sideral, fixado nas estrelas concretas das constelações plasmadas no céu (mesmo quando estas últimas foram "normalizadas" no seu tamanho sob a forma de signos), é o mais antigo e continuará a ser utilizado por muito tempo na prática astrológica. O tropical, vinculado às estações do ano (aos equinócios e solstícios) tem origem grega e revela uma abordagem matemática relacionada com questões calendáricas e astrométricas (proporcionando um sistema de coordenadas para medir longitudes rigorosas). Será divulgado por Ptolomeu e assim ganhará visibilidade. A
analogia com o movimento de um corpo segundo um percurso circular
definível relativamente a um centro (órbita) não era feita pelos
astrónomos babilónicos, principalmente preocupados com o retorno de
determinados fenómenos a certas direcções no céu, calculando a sua
periodicidade. Não há uma "eclíptica" nem uma "esfera celeste" como na
geometria esférica grega. Como Noel Swerdlow enfatizou: "While it is conventional to call locations and distances measured in signs and us [uma medida de comprimento] 'longitude', one should not take this to be a coordinate, in the sense
of Ptolemy and modern astronomy, measured along the ecliptic or even a
circle." (The Babylonian Theory of the Planets, Princeton University Press, 1998, p.34). A ideia de um movimento contínuo ao longo de um percurso circular é totalmente irrelevante para a prática babilónica. Portanto, os babilónicos e os gregos não concebiam o [mesmo] zodíaco da mesma maneira. E quando falamos da esfera, estamos a presumir uma concepção grega, que antes não existia. Podemos
estabelecer uma sequência desde que no séc. V a.C. foi definida a
divisão duodecimal que assumirá intervalos iguais de 30º cada
(espelhando um ano esquemático de 12 meses com 30 dias cada, no qual o
Sol se deslocaria aproximadamente o "comprimento" de 1 uS [o que virá a equivaler a 1 grau] por dia), até ao séc. III quando já se inserem longitudes em graus (v. Abraham Sachs, A Late Babylonian Star Catalogue,
Journal of Cuneiform Studies 1952, 6, pp.146-50). A 'astronomia
científica' babilónica, que recorria exclusivamente a métodos
aritméticos, utilizava uma eclíptica fixa em relação às estrelas, isto
é, as distâncias ao longo desse "caminho" eram siderais, determinadas a
partir de uma estrela arbitrária nas suas imediações (Peter Huber, Ueber den Nullpunkt der Babylonischen Ekliptik,
Centaurus, 5 (1958), 192-208) Portanto, na Babilónia não se
privilegiavam os equinócios e solstícios, enquanto, por contraste, o
zodíaco grego assumirá como referência o Ponto Vernal (com variantes quanto ao grau específico, como veremos). Na Mesopotâmia, o "ponto zero" de uma medição geralmente (e obviamente) não coincidia com o equinócio vernal. Como
Huber salienta, as posições planetárias eram quase sempre observadas a
partir de estrelas de referência, chamadas "Normais" (i.e. normativas) na literatura científica: "die Babylonier die Planetenpositionen fast durchwegs relativ zu den Normalsternen beobachteten" (ibid.,
p.207). Não foram encontrados registos babilónicos especificando um
procedimento para localizar as divisões dos signos. Existem algumas
referências de fontes helenísticas posteriores que afirmam que Antares
e Aldebaran (exemplos úteis pois são estrelas brilhantes perto da
eclíptica, estando diametralmente opostas) se situavam em posições
centrais de 15° (em cada um dos respectivos signos), e.g.
por Cleomedes (séc. IV). Considerando todas as estrelas cujas
coordenadas puderam ser claramente derivadas a partir de diversas
fontes (listagens, "almanaques", etc.) e que podia aferir, Huber obteve uma correcção média do "ponto zero" para a epoch -100 de 4º 28’ (mais ou menos 20’). Esta seria (para a época em causa) a diferença para um nocional zodíaco tropical (o diferencial a que se chama "Ayanāṃśa" na astrologia indiana). Segundo Geminus (séc. I
a.C.): "Não há qualquer diferença entre os Gregos e os Caldeus [i.e. povos da Mesopotâmia] excepto
na divisão dos signos, uma vez que o primeiro ponto dos signos não se
sujeita à mesma regra para eles: entre os Caldeus, eles precedem por 8
graus." (Aujac, G., Introduction aux Phénomènes, 1975), I.9, p.3 [trad. nossa]). Segundo Dekker (Op. cit., pp.15-9), o primeiro astrónomo a comentar e utilizar inequivocamente "Ari 0º" (i.e. o início de Aries coincidente com o ponto vernal)
foi Hiparco
(c.190-c.120 a.C.), que nos informou de que era uma prática dos 'antigos'
(referindo-se provavelmente a Euctemon, c. 430 a.C., e Callipus, c. 330
a.C., que se supõe terem colocado os pontos pivotais,
equinócios e solstícios, no início dos respectivos signos nos seus
'parapegma', calendários nos quais os dias eram contados de acordo com
o movimento do Sol (podemos considerá-los "antepassados" dos almanaques).
O mesmo sistema (Ari 0º) será utilizado por Ptolomeu e deste ganhará o prestígio e a futura visibilidade. Tornou-se a única convenção significativa em termos de cartografia celeste. Quanto à variante Ari 8º, Otto Neugebauer sugeriu que estaria relacionada com a prática babilónica do cálculo de efemérides lunares (i.e. com expedientes da teoria lunar babilónica), a que chamou 'System B' (Neugebauer, A History of Ancient Mathematical Astronomy (abrev. HAMA), 1975, pp. 368, 594–6). Independentemente da origem, a convenção Ari 8º será popular entre autores Romanos (e.g., Vitruvius, Varro (Varrão), Hyginus, Plinius, Martianus Capella), perpetuando-se pela sua influência ao longo da Idade Média. Demais, são referidos diversos pontos para o início do Verão (solstício estival no Hemisfério Norte): Cnc (i.e. Cancer) 0°, Cnc 8°, Cnc 12°, ou Cnc 15°. Para a versão "Cnc 12º" nunca foi encontrada qualquer explicação, especulando-se que talvez recuasse a um qualquer ponto mediano nos meses lunares esquemáticos (convencionais) babilónicos. Quanto ao 15º (ponto intermédio do signo), Hiparco argumentou que fora utilizado por Eudoxus na colocação de equinócios e solstícios, não se apercebendo que o seu antecessor os colocava no meio das constelações (i.e. das estrelas aparentes, observáveis) e não dos signos (que resultam de uma divisão convencional da Eclíptica que Eudoxus, tudo indica, nem sequer utilizava).
O sistema de coordenadas baseado no plano equatorial mede-se em graus de Ascensão Recta (ascensio recta) ao longo do Equador Celeste e em graus de Declinação perpendiculares a esse círculo máximo, v. infra. A Ascensão Recta
é habitualmente expressa em horas e minutos, 1 hora equivalendo a 15
graus, 4 minutos-tempo a 1 grau. Uma vez que o Sol percorre (e de facto
materializa) a Eclíptica (e não o Equador) a sua Declinação (variação norte-sul justamente em relação ao Equador) varia de acordo com a sua distância aos pontos equinociais (Aries e Libra). Assim alcança dois pontos extremos: quando chega ao mais elevado (no signo de Cancer) ou ao mais meridional (em Capricornus), diz-se que está num “Trópico” (tropikós,
que significa "relativo a uma volta" ou "relativo ao regresso,
retorno"; como se duma "estação" se tratasse, equivalente latino dá
origem à palavra “solstício”: quando o Sol pára). A partir daqui, o astro retrocede e volta a "descer" ou a "subir" (dependendo se chegou ao Trópico de Câncer ou ao Trópico de Capricórnio, i.e., ao Solstício de Verão ou ao Solstício de Inverno, respectivamente). São chamados 'cardeais' os signos (Aries, Cancer, Libra e Capricornus) que marcam o início das Estações do Ano. Convém compreender que os signos são intervalos de longitude eclíptica e não as constelações 'reais' que ab initio lhes emprestaram o nome; trata-se, numa perspectiva que recua pelo menos a Hiparco e que será popularizada por Ptolomeu (séc. II), de um zodíaco ‘tropical’ (vinculado aos pontos equinociais e solsticiais) e não ‘sideral’ (vinculado à posição verdadeira das estrelas). O lento deslocamento devido ao mencionado fenómeno de precessão foi no passado calculado com o recurso à longitude da primeira estrela de Aries na listagem de Ptolomeu: prima Arietis ("arietis precedens sive prima arietis"), γ (Gamma) na classificação que Johann Bayer utilizou no seu importante atlas de 1603. Válida para determinada data raíz (a que hoje chamamos “epoch”). Era a estrela visível a olho nu mais próxima do Ponto Vernal. A sua longitude dada por Tycho Brahe, para 1600, era de 27° 37'. O valor dessa constante era importante pois (quando somado) actualizava, para a data específica, as longitudes estelares previamente catalogadas. Copernicus media as longitudes a partir da prima Arietis, cf. Rosen (trans), Three Copernican Treatises, Dover Publications, 1958 [1939], p.126, n.73; J. L. E. Dreyer, A History of Astronomy..., p. 330). Contestando o método ptolomaico, o astrónomo (no seu Commentariolus) afirma que, uma vez que os equinócios e restantes "pontos do universo" se deslocam consideravelmente ao longo do tempo, quem procura deduzir a duração mediana da revolução anual (duração do ano trópico) cai necessariamentente em erro. Segundo o seu discípulo Rheticus: "We must accordingly imagine a mean equinox moving in precedence from the first star of Aries in the sphere of the fixed stars, and displacing them by its uniform motion." (Narratio prima, in: E. Rosen (trans.), Three Copernican Treatises, Op. cit., p.115). Uma pequena imprecisão no Calendário Juliano (cuja duração assumida para o ano trópico era 11 minutos e 14 segundos mais pequena do que 365 dias e 6 horas) determinava que a data de entrada do Sol no signo de Aries acontecesse gradualmente cada vez mais cedo, em Março. Em termos gerais, e salvaguardando pequenas flutuações, J. C. Eade tabulou os seguintes intervalos de anos e os correspondentes dias do equinócio (Op. cit., p.11). Este afastamento relativamente às Estações do Ano será uma das motivações para a correcção que no séc. XVI instaurou o Calendário Gregoriano que ainda hoje utilizamos.
O círculo máximo (ou "grande círculo") que liga os pólos da Eclíptica, os pólos do Equador Celeste e passa pelos primeiros pontos dos signos de Cancer e Capricornus é chamado Coluro Solsticial; o que passa nos primeiros pontos de Aries e Libra é chamado Coluro Equinocial. Os coluros já haviam sido definidos por Hiparco (Comm. in Aratus,
117). Foram assim chamados porque "é como se as suas 'caudas' tivessem
sido cortadas, uma vez que não conseguimos observar as partes destes
que começam no antárctico, paralelo sempre invisível" (Isagoge 27, Ernst Maass, Comm. in Arat., 60), v. Toomer, Ptolemy's Almagest, p.19. Ou seja, são círculos truncados, porque nunca se observa parte deles (sempre abaixo do horizonte).
A Ascensão Recta entrou na astronomia por via do problema dos tempos ascensionais (v. infra), i.e. quanto tempo demorava um signo a ascender no horizonte Leste? Era também utilizada para referir o grau do Equador Celeste que chegava ao Meridiano (o círculo máximo que corre de norte a sul passando pelo zénite do lugar em simultâneo com um determinado grau da Eclíptica. A relação da Ascensão Recta com a Longitude Eclíptica (que é medida ao longo desse círculo oblíquo tendo como referência ou origem o Ponto Vernal) não se altera com a latitude do lugar, logo pode ser tabulada definitivamente assim que se defina ou conheça qual o valor da Obliquidade da Eclíptica (deste a Antiguidade que se sabe que este valor, que equivale à declinação do Sol nos solstícios, decresce gradualmente). Todavia, o grau específico do Equador Celeste que cruza a linha do horizonte varia com a latitude do observador: é a chamada Ascensão Oblíqua (ascensio obliqua, o arco do Equador que ascende em simultâneo com o arco da Eclíptica compreendido entre os ponto Vernal e o ponto Ascendente, ver esquema de R. Pottenger infra), um valor útil pois era exactamente 90º maior do que a Ascensão Recta do Meio-Céu astrológico. Em desuso na Astronomia moderna. A Ascensão Oblíqua é menor do que a Ascensão Recta no arco Aries - Virgo e maior no arco Libra - Pisces. Um último sistema, este de coordenadas locais, define-se através das variáveis Altura e Azimute. A posição de um corpo celeste pode ser determinada em relação à localização específica, local, sendo a grelha utilizada definida pelo Horizonte do observador e pelo Meridiano (i.e o semi-círculo visível que corre de norte a sul passando pelo zénite). Assim, a posição é definida por um sistema de círculos paralelos de altitude (almocântaras) e, no noutro eixo, pelo azimute, distância angular medida ao longo do círculo do Horizonte a partir de um ponto fixo convencional (hoje habitualmente a partir do ponto geográfico Norte e medindo o arco na direcção Este - Sul - Oeste). A latitude terrestre de um lugar pode ser definida pela elevação do pólo celeste, a sua altura acima do Horizonte (comodamente medida pela altura da Estrela Polar, actualmente muito próxima do pólo). Dada a altura do pólo e a direcção Norte-Sul geográfica, o ponto de intersecção entre o Meridiano e o Equador Celeste é facilmente determinado. É, por definição, um ponto do Meridiano 90 graus distante do pólo. Ou seja, é o complemento da latitude do lugar (e.g., em Aveiro, elevação do pólo: 40ºN, o Equador Celeste intersecta o Meridiano num ponto 50 (90 - 40) graus acima do horizonte sul). Consequentemente, também é fácil determinar as alturas meridianas do Sol (máxima e mínima) ao meio-dia verdadeiro. Pois sabemos que o Sol não se afasta mais do que 23,5 graus para norte ou para sul do Equador Celeste (o que acontece nas datas dos solstícios). No exemplo aveirense, teremos como extremos (50 + 23,5 =) 73,5 graus em Junho e (50 - 23,5 =) 26,5 graus em Dezembro. Por outro lado, sabendo a altura meridiana do Sol e a co-latitude (ângulo complementar da latitude, i.e. a diferença entre a latitude e 90°) do lugar geográfico saberemos a declinação do Sol. Todavia, tal como com a altura do Sol, informação é insuficiente para saber o dia do ano em causa pois será necessário saber em que etapa do seu percurso o Sol está, se a “subir” ou se a “descer”.
- Um
"círculo máximo" é assim designado pois possui a maior dimensão
possível na superfície de uma esfera, dividindo-a a meio. O seu centro
coincide com o centro da esfera. Os grandes círculos são utilizados
como referência para os sistemas de coordenadas cometidos à localização
dos corpos celestes.
- O Equador Celeste divide o Horizonte do observador a meio. Os pontos
deste círculo não possuem Declinação. Um ponto aí situado cruza o
Meridiano local segundo um ângulo recto. Desloca-se no céu a uma
velocidade uniforme de quase 1º em cada 4 minutos de tempo (360º em
23h54m). Nos dois Equinócios, o Sol está no exactamente no Equador e
permanece a mesma quantidade de tempo acima e abaixo do horizonte, fazendo com que os dias e as noites tenham a mesma duração.
O Horizonte Celeste é definido pelo plano que passa através do centro da Terra, perpendicular à recta que passa pelo zénite e pelo nadir. Os pontos cardeais no Horizonte são chamados Ponto Norte (para distinguir do Pólo Norte), Ponto Este (ou Leste), Ponto Sul (para distinguir do Pólo Sul) e Ponto Oeste. O Primeiro Meridiano é específico para cada observador, sendo o círculo máximo que passa pelos pólos e pelo zénite. - O movimento diurno aparente é chamado Movimento Primário (i.e. o do Primum Mobile
na antiga perspectiva geocêntrica) e verifica-se de Leste para Oeste. O
movimento do Sol e dos planetas é ao contrário, de Oeste para Leste
(excepto nas retrogradações ocasionais dos planetas), é chamado
Movimento Secundário. O do Sol acontece num círculo máximo a que
chamamos "Eclíptica". Este círculo surge inclinado em relação ao Equador
Celeste (por isso falamo da Obliquidade da Eclíptica).
Assim, enquanto o Equador Celeste intersecta o Horizonte exactamente
nos pontos que definem as posições geográficas Leste e Oeste, a
Eclíptica aparecerá tipicamente "inclinada", o seu ponto nascente
algures para Nordeste e o poente para Sudoeste ou, inversamente, o seu
ponto nascente para Sudeste e o poente para Noroeste. A única excepção
acontece, diariamente, quando os pontos equinociais (intersecção do
Equador Celeste com a Eclíptica) se encontram exactamente no Horizonte,
sendo que nestas circunstâncias a Eclíptica nasce na exacta direcção
Leste e se põe na direcção Oeste.
- Devido à Obliquidade da Eclíptica, os graus do Zodíaco nascem e têm o seu ocaso em diferentes pontos do Horizonte (i.e. em diferentes Azimutes). Cada grau descreve pois um arco específico, paralelo ao Equador Celeste, através do céu, nascendo algures no horizonte leste, culminando no Meridiano (rigorosamente a Sul, para um observador no Hemisfério Norte) e tendo o seu ocaso algures no horizonte oeste. É o chamado 'Arco Diurno' desse grau. O Arco Diurno é complementado pelo Arco Nocturno. O Círculo Diurno é o total. Os pontos de orto (nascimento) e ocaso de um grau são sempre equidistantes do Meridiano (i.e. o Meridiano divide qualquer Arco Diurno em dois Semi-Arcos).
- A Obliquidade da Eclíptica está também relacionada com as posições dos
círculos polares (paralelos de declinação, Ártico e Antárctico) e com o
fenómeno da 'circumpolaridade': os astros que nunca nascem ou nunca se
põem.
- Os
adjectivos "cósmico" e "crónico" dizem respeito ao nascer e ao ocaso do
Sol, respectivamente. Por um pequeno período de tempo, uma estrela que
nasce com o Sol ("cosmicamente") terá o seu ocaso com o Sol
("cronicamente"). Uma estrela põe-se "cosmicamente" quando o Sol nasce,
ou nasce "cronicamente" quando o Sol se põe. Claro que com o movimento
do Sol através das estrelas, estará em causa o nascimento helíaco
(quando o astro se torna visível imediatamente antes do nascer do Sol).
- A Ascensão Recta de um objecto é o ângulo entre o Ponto Vernal (um dos dois pontos de intersecção da Eclíptica com o Equador Celeste, aquele em que o Sol se encontra no Equinócio de Março) e o meridiano desse objecto, medido sobre o Equador Celeste, na direcção Leste. A Ascensão Oblíqua de um grau zodiacal é simplesmente o ponto do Equador Celestial (i.e., o grau de Ascensão Recta) que com ele nasce em simultâneo. Assim chamado porque o Horizonte, ao contrário do Meridiano, não intersecta o Equador perpendicularmente (segundo ângulos rectos) mas sim obliquamente. De modo similar, a Descensão Oblíqua é o ponto do Equador Celeste cujo ocaso acontece em simultâneo com o grau zodiacal, no hozonte oeste.
N.B.: No Almagesto de Ptolomeu, o Equador é, literalmente, o "círculo de dia igual" ou "equivalente". O Meridiano é o "círculo do meio-dia", obviamente. A Eclíptica é o "círculo inclinado", etim.: "o que passa pelo meio dos signos do Zodíaco".
As Coordenadas Equatoriais Actualmente, o sistema privilegiado para localizar um objecto (por exemplo, uma estrela) é um sistema de cordenadas análogo ao das coordenadas geográficas (Latitude e Longitude). Na Esfera Celeste essas coordenadas têm o nome de Ascensão Recta e Declinação. São as Coordenadas Equatoriais.
Este sistema adapta-se ao "movimento natural" das estrelas. Em regiões de latitude intermédia, algumas estrelas têm nascimento e ocaso, algumas permanecem 24 horas acima do horizonte, outras permanecem 24 horas abaixo do horizonte.
As estrelas visíveis descrevem no céu arcos com uma certa inclinação em relação ao horizonte, a qual depende da latitude do lugar. O sistema de coordenadas utiliza a mesma ideia das coordenadas geográficas (latitude e longitude). Imagine-se, com vimos, a Esfera Celeste "contendo" a esfera terrestre. O equador terrestre, projetado para o firmamento, desenha o Equador Celeste. O eixo de rotação da Terra, prolongado, forma os pólos celestes. A linha que vai do pólo norte ao pólo sul celeste e que passa sobre a cabeça de um determinado observador, constitui o meridiano local deste observador (o Sol está no Meridiano ao Meio-Dia, daí esta designação). Podemos entender o meridiano como a projecção da linha da longitude local sobre o firmamento. Em Geografia aprendemos que a determinação da latitude é fácil, conhecendo-se pólos e Equador. Para a origem da Longitude foi necessário estabelecer, por convenção, um primeiro meridiano de referência (Greenwich) como longitude zero. Na Esfera Celeste, estabelece-se um determinado ponto entre as estrelas, chamado Primeiro Ponto de Aries ou Ponto Vernal, como origem. Esse ponto corresponde a um dos pontos de intersecção da Eclíptica com o Equador Celeste, aquele em que o Sol se encontra no Equinócio de Março (Vernal ou de Primavera, no Hemisfério Norte), quando passa do hemisfério sul para o hemisfério norte celeste. É
a Primavera, essa "manhã" na qual a natureza reverdece (no Hemisfério
Norte, obviamente). A eloquência de Garrett Serviss descreveu-a assim:
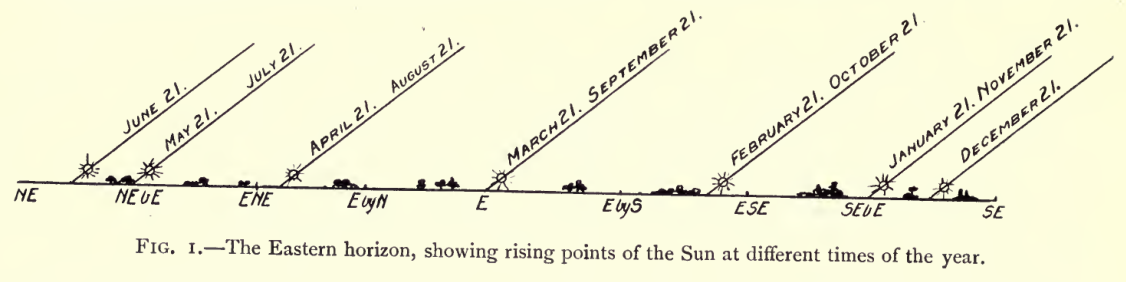 O Sol nasce no Horizonte Leste em diferentes pontos ao longo do ano (Annie & E. Walter Maunder, The Heavens and Their Story, London, Robert Culley, 1908, Fig.1, p.31) O exemplo seguinte (clicar no esquema para ampliar) constitui uma proposta observacional pedagógica
e representa (para determinado local específico) os fenómenos locais do
Sol ao longo do ano. Da periferia para o centro do esquema: as datas,
azimutes dos ortos e ocasos, o ângulo do Sol em relação ao horizonte, a
declinação solar e, por fim, a hora aproximada do nascimento ou do
ocaso (ao modo astronómico, sem pontos ou letras, e.g., "2000" = 20h00)
Mills, H. Robert, Practical Astronomy: A User-friendly Handbook for Skywatchers, Albion Publishing, 1994, p.95 Nos textos mais antigos aprendemos que as estações do ano (nas nossas latitudes) se dividem em "Veraõ, Estio, Outono & Inuerno". A palavra "primavera" deriva do latim tardio "prima vera", plural de "primus ver" (raíz vēr, vernus, daí "vernal"). O elemento "vēr" (relacionada com o gr. "éar") está na origem da palavra "Verão". Como Marco Neves explica acerca da palavra "Verão" (in Ciberdúvidas da Língua Portuguesa), a palavra Primavera
significa, portanto, "primeiro Verão", a primeira parte da estação
quente. É corrente (e coerente), encontrar nos textos antigos as
estações elencadas como Verão, Estio, Outono e inverno. O excerto
seguinte é dos Libros del Saber... (séc. XIII):
 Na imagem acima, exemplo em Português. (Fr. Antonio Teixeira, Epitome das Noticias Astrologicas para a Medicina (1670), p.125)
A
latitude geográfica do observador determina a altura do Equador
Celeste, bem como a sua inclinação relativamente ao Horizonte (leste e
oeste). Quanto menor a latitude, maior o ângulo. Na latitude 0º
(Equador), o Equador Celeste é perpendicular ao Horizonte e passa pelo
zénite do observador. O Sol percorre obviamente a Eclíptica e os
planetas estão sempre aí ou na sua proximidade (obliquidade desse
círculo é causada pela inclinação do eixo da Terra). A ilustração
exemplifica a observação vespertina (no "poente") de um planeta inferior
(Mercúrio ou Vénus) e a sua elongação em Março e em Setembro, a partir
de uma latitude norte intermédia. A direcção do movimento diurno
aparente, resultante da rotação da Terra (indicado aqui pela seta
"direction of setting") é, para qualquer astro, paralela ao Equador
Celeste. Verificamos que em Março o planeta se observa mais elevado
relativamente ao Horizonte local porque a Eclíptica faz um ângulo
maior com este último. No equinócio vernal, o Sol está precisamente no
Equador e "viaja" para norte. Consequentemente, a Eclíptica está mais
elevada adiante da sua posição. Em Setembro, quando o Sol já "viaja"
para sul, acontece o inverso e o planeta observa-se menos elevado.
(Muirden, J., The amateur astronomer's handbook, (3rd ed.), New York : Harper & Row, 1983)
- Declinação (DEC ou δ) de um objecto é a sua distância angular para Norte ou Sul da Equinocial (Equador Celeste), medida ao longo do meridiano onde esse objecto se encontra. É análoga à Latitude terrestre. No Equador Celeste: δ = 0°. As Coordenadas Eclípticas Longitude e Latitude são termos utilizados em relação às coordenadas eclípticas, i.e. baseadas na Eclíptica e nos seus pólos. A Longitude (λ) é medida nesse círculo para Leste a partir do Ponto Vernal, a Latitude (β)
é a distância para Norte ou Sul da Eclíptica, medida não nos meridianos
mas em círculos perpendiculares à Eclíptica e que passam pelos pólos
desta. O círculo máximo de referência define o caminho aparente do Sol
ao longo do ano, no meio atravessando o fundo de estrelas que também acolhe, com maior ou menor aproximação, o percurso da Lua e dos planetas: o Zodíaco, faixa dividida segundo o número de meses em doze partes ou Signos. O sistema eclíptico é, portanto, particularmente conveniente para representar os movimentos dos planetas. As Coordenadas Horizontais
Entretanto, em função do horizonte, o ponto que fica na vertical do observador (na sua perpendicular), chama-se zénite; o ponto infra, diametralmente oposto é chamado nadir (do Ár. "nazir"). Um sistema complementar óbvio é o Sistema Horizontal de coordenadas Altazimutais, que não é "absoluto" mas apenas local: a altitude é medida a partir do plano do horizonte; o azimute convencionalmente a partir do ponto norte do horizonte, na direcção do leste. A grelha aqui utilizada é definida pelo Horizonte do observador e pelo Meridiano (ou melhor: pelo seu semi-círculo que corre de norte a sul passando pelo zénite).
- Horizonte aparente versus Horizonte ideal ou racional: o aparente é o observável, variável; o "ideal" ou astronómico divide a Esfera Celeste precisamente em dois hemisférios, sendo uma linha que dista 90º do zénite. N.B.: o dia astronómico começava ao meio-dia. Era usual considerar a duração (em horas e minutos) do arco semi-diurno (i.e. metade da duração do dia artificial [que é o intervalo entre o nascimento e o ocaso do Sol] para determinada data em determinada latitude). Daqui se podem extrapolar as horas do orto e ocaso do Sol, a duração do dia (artificial) e da noite e o tamanho das horas sazonais (diurnas e nocturnas). O grau zodiacal ocupado pelo Sol era utilizado para identificar o dia específico. Os documentos que compilavam informação astronómica posicional eram as Tabelas, as Efemérides e os Almanaques, seguindo decrescente complexidade. As tabelas historicamente mais relevantes no contexto Latino foram as de Toledo (c. 1080), as Afonsinas (c. 1270), as Pruténicas (1551) e as Rudolfinas (publicadas pela primeira em 1627). Estas compilações eram entendidas como "perpétuas" no sentido em que disponibilizavam conjuntos de valores (uma "tábua" para o motus médio do planeta para cada século, outra para os anos intermédios, correcções para as inequalidades, etc.) a partir dos quais as posições dos planetas podem ser calculadas. Jã as Efemérides diziam respeito a um período confinado, fornecendo as longitudes planetárias (e.g., para as 0H00 ou para o meio-dia) para cada dia e as latitudes, habitualmente, em intervalos de 10 dias. Por fim, os Almanaques, modalidade mais popular de disseminada, fornecerão uma miscelânea de informações, baseando-se no calendário litúrgico, no calendário das estações e nas lunações. Voltados para a vida quotidiana e para um público não especializado.
A Esfera Celeste roda (aparentemente) sobre o respectivo eixo uma vez
em cada 23 horas e 56 minutos (mais especificamente 23h 56m 4s). É o Dia Sideral,
medido em função da direcção de qualquer estrela distante, na direcção
rigorosa da qual estaremos de novo após esse intervalo.
O Dia Sideral pode ser medido pelo intervalo de duas culminações sucessivas de qualquer estrela (culminação real e náo a aparente, pois existe o efeito - diminuto, é certo -, do movimento próprio das estrelas). Mas este período é mais pequeno do que o Dia Solar Médio de 24 horas devido ao movimento orbital da Terra (translação). Durante o intervalo de que a Terra precisa para efectuar uma rotação de 360º, avançou quase 1º na sua órbita em torno do Sol. Deste modo, para fazer retornar o Sol ao mesmo ponto quando observado no céu (definição de "dia"), a Terra precisa efectuar a rotação adicional dessa fracção de grau. Os cerca de 4 minutos de diferença determinam o gradual movimento cíclico através do qual as estrelas parecem chegar ao meridiano 4 minutos mais cedo todos os dias. Por isso vamos observando diferentes estrelas à mesma hora, ao longo do ano. O movimento de translação e a paralaxe
A Eclíptica representa o plano orbital da Terra. O seu ângulo relativamente ao Equador Celeste é determinado pela inclinação do eixo do planeta relativamente a esse plano.
O "carrocel" do Zodíaco: "...faixa onde a Ciência, a Pseudo-Ciência, a História e a Mitologia inexoravelmente se entrelaçam" (Nourse, A. E., The Backyard Astronomer, Franklin Watts, 1973, p.31).
O deslocamento do Sol ao longo das constelações zodiacais deve-se ao
movimento de translação do planeta. Ilustração do percurso (aparente) do astro ao longo do Zodíaco (na representação, o Sol estaria "em Libra", a Balança). (Cromo de álbum
editado em 1966 pela Agência Portuguesa de Revistas)
Incidentalmente, a translação do nosso planeta permite utilizar uma útil ferramenta de medição: a paralaxe. Trata-se de um fenómeno que podemos observar no nosso quotidiano, como se pode compreender na ilustração seguinte, na qual se observa (alternadamente com cada um dos olhos) um cenário de fundo segurando um lápis como "referente" próximo.
Utilizando dois pontos diametralmente opostos da órbita, é possível determinar a alteração de posição de uma estrela próxima relativamente às estrelas mais distantes em "fundo". A primeira determinação deve-se a Friedrich Wilhelm Bessel (em 1838 mediu a distância à estrela 62 Cygni). Um 'parsec' (segundo de arco de paralaxe), equivale a 3.26 anos-luz. Historicamente, a ausência de paralaxe óbvia nas estrelas foi uma das grandes perplexidades na afirmação da Teoria Coperniciana. Tycho Brahe estimou que para explicar a ausência de paralaxe anual das estrelas (importante argumento contra o movimento de translação), as estrelas deveriam estar pelo menos a 700 vezes a distância de Saturno. Todavia, Galileu confirmou telescopicamente que as estrelas estão muito longe pois, ao contrário dos planetas, não se observam como discos, ou seja, continuam a ver-se como simples pontos. A escala do Universo foi, ulteriormente, reconsiderada. Na prática, os astrónomos profissionais actuais utilizam como medida de distância o parsec e seus múltiplos (e raramente o ano-luz). Com origem convencional, é a distância a um objecto cujo ângulo de paralaxe é de um segundo de arco (o nome "parsec" combina e abrevia "paralaxe" e "segundo de arco", arcsecond em Inglês). A paralaxe de uma estrela, como o termo é habitualmente utilizado, é a heliocêntrica. Significa que se implementa uma correcção nas medições a partir da Terra, resultando na prática em cerca de metade do maior deslocamento observado. O método da paralaxe somente pode ser utilizado até distâncias de cerca de 100 anos-luz; medições mais remotas baseiam-se noutros métodos, e.g., no diferencial entre as magnitudes aparentes e absolutas.
A determinação da paralaxe de um corpo celeste recorre ao método
da triangulação, a partir da distância base conhecida (AB). Baseando-se
no princípio de que a soma dos ângulos internos de um triângulo é
sempre 180º. (Simon Newcomb, Astronomy for Everybody, McLure, Philips & Co., 1904)
Ilustração seguinte exemplifica a determinação da distância da Lua por este método, determinando o deslocamento paraláctico entre dois sítios de observação afastados milhares de quilómetros entre si (um em cada hemisfério). Como dois olhos de uma cabeça gigantesca, cada qual observando a Lua (em simultâneo) numa direcção diferente. A posição do satélite será determinada pelas distâncias ao zénite de cada observador, enquanto as distâncias AC e BC são conhecidas (equivalem ao raio do nosso globo). Através da trigonometria, será fácil calcular os outros ângulos, bem como o comprimento da linha recta do centro da Terra à Lua. No caso do Sol, distância base seria, ainda assim, demasiado exígua. A distância AB (linha-base) é calculada à partida.
C é o centro da Terra. A e B os dois pontos de observação, um em cada hemisfério da Terra. M é a Lua. As linhas CZ e CZ' indicam as direcçóes dos zénites de A e B, respectivamente. Subtraindo 180º a cada ângulo medido (em A e em B, ver "angle measured" para cada um dos pontos no esquema), determinamos os ângulos internos nestes dois pontos. O ângulo em C equivale à soma das latitudes de A e B (porque situados em sítios opostos do Equador). Com estes 3 ângulos conhecidos, o ângulo em M determina-se simplesmente subtraindo 360º à soma dos anteriores. (Serviss, G., Astronomy in a Nutshell, G. P. Putnam's Sons, 1912)
Tal como a Paralaxe, a Aberração da Luz é um efeito do movimento orbital da Terra, contudo maior e independente da distância do objecto. Radica no movimento da Terra no espaço. A posição do observador altera-se (de modo diminuto, em termos práticos) em relação ao ápex da velocidade da terra no instante da observação.
Ascensões ("ascendimentos") e descensões dos Signos Bouché-Leclercq resumiu admiravelmente a problemática da conversão os graus (zodiacais) de ascensão oblíqua em graus (equatoriais) de ascensão recta: "(...) les signes du Zodiaque montant au-dessus de l'horizon et descendant au dessous plus ou moins obliquement, leur vitesse angulaire ne peut être mesurée que sur le limbe de la grande roue cosmique, celle dont le plan est perpendiculaire à l'axe de rotation, c'est-àdire sur l'équateur. Il s'agit donc de convertir les degrés d'ascension oblique (Zodiaque) en degrés d'ascension droite (Equateur). L'obliquité du Zodiaque par rapport à l'équateur est un élément fixe du problème : il y en a un autre, variable suivant la latitude du lieu d'observation, c'est-à-dire l'angle que fait l'horizon du lieu avec le plan de l'équateur et celui de l'écliptique ou ligne médiane du Zodiaque. Cet élément variable est cause que, tous les calculs une fois faits pour un « climat » (latitude), il faut les recommencer pour un autre climat." (L'Astrologie Grecque, Paris: E. Lerous, 1899, p.262) As ascensões oblíquas, outrora importantes para a interpretação dos movimentos da Esfera, já não são utilizadas na Astronomia (são todavia pertinentes nas elucubrações astrológicas). Eram ensinamento canónico nos contextos helenístico e medieval, devido à importância dos tempos de orto (quando um ponto se eleva ou ascende na esfera oblíqua). [Sphaerica é, como sabemos, o nome do tratado de Menelau de Alexandria (c. 100 AD), que inclui os teoremas necessários para o cômputo dos tempos ascensionais ou "anafóricos" (αναφοραί)]. O já citado Bouché-Leclercq comentou: "[Ademais], já sabemos quão laboriosa era [no passado] a conversão dos graus do Zodíaco em graus de ascensão recta, medidos sobre o equador, conversão indispensável sempre que se tratava de avaliar a duração. Era a propósito deste cálculo que os astrólogos proficientes lançavam o seu desdém sobre os ignorantes." (Op. cit., p.419, [trad. nossa]). Cleomedes (Gr. Κλεομήδης) referiu-se à diversidade dos tempos ascensionais dos signos: "So if all the dõdekatèmoria [i.e. os signos, cada qual 1/12 do círculo] of the zodiacal circle, which are equal, also rose in an equal time, every interval of a nighttime and a daytime would consequently be equal as well. But in fact the summer signs rise upright and set obliquely, and as they rise upright the period of their rising is longer, and so the parts of them through which the Sun goes in the interval of a nighttime and a daytime rise proportionately more slowly. But the opposite occurs with the winter signs." (Meteõra [Lat. Caelestia], I.4; Alan C. Bowen and Robert B. Todd (ed., trans.), Cleomedes’ Lectures on Astronomy, University of California Press, 2004) Pedro Nunes, na sua tradução e comentário do texto do Tratado da Sphera... (Lixboa: per Germão Galharde, 1537) resume, afirmando que qualquer que seja a época do ano e o tamanho dos dias (artificiais, i.e. intervalo entre o orto e o ocaso), nascem sempre seis signos de dia e seis de noite. Conclui-se que uma hora natural (ou sazonal) equivale ao tempo que meio signo demora a elevar-se (doze horas naturais = 6 signos). À diferença no tamanho destas horas (que são variáveis ao longo do ano, ao contrário das equinociais ou iguais), corresponde o modo como os signos "específicos" (i.e. nesse dia e latitude particular) se elevam: se direitos ("por recto nascime[n]to") ou oblíquos ("tortos"), ou seja, quais são, quantos se elevam directamente e quantos obliquamente: "Porque a regra he que por grãde ou pequeno que ho dia ou noite seja: seys signos nacem de dia, e seys de noite: nem nacem mais nem menos: ora os dias ou as noytes sejam grandes ora pequenos. E daqui se toma que poys a [h]ora natural he espaço de tempo em que na[s]ce a metade de um signo: tera ho dia arteficial doze [h]oras naturais: e outras tãtas da noite. Em todollos outros circulos de hua banda da equinocial [Equador Celeste] ou da outra sam os dias mayores: ou menores: e assi mesmo as noites segundo que mais signos ou menos nascem dereytos ou obliquos: assi no dia como na noyte." Na tradição horoscópica mais amadurecida, a determinação do Ascendens (o Ascendente de um horóscopo ou thema, i.e. o grau exacto do Zodíaco que se eleva no horizonte leste) dependia dos tempos ascensionais dos signos, e estes, por sua vez, da latitude do lugar, devido à obliquidade da Eclíptica relativamente ao Equador Celeste. Muitos astrólogos menos proficientes limitavam-se a convencionar exactamente duas horas por signo, o "método vulgar de cálculo", mencionado por Manilius, obviamente muito impreciso (vide Tester, A History of Western Astrology, Boydell Press, 1999 (1987), p.39). Um erro comum, tanto em alguma tratadistica como em interpretações dos textos, é assumir que os quatro cardines ou anguli (ASC, MC, DSC, IC, usando as abreviaturas actualmente comuns) dividem a Eclíptica em arcos exactamente iguais (nas latitudes intermédias, onde se incluem as historicamente relevantes). Assume-se, ainda, que o Medium Caeli equivale ao zénite do observador (ponto perpendicular, o mais elevado da esfera celeste local) e o Imum Caeli se situa directamente sob os seus pés. Na realidade o Medium Caeli é, evidentemente, o ponto de intersecção, acima do Horizonte, da Eclíptica com o Meridiano. Convém compreender que o Horizonte e o Meridiano estão fixos na perspectiva do observador. O Zodíaco move-se "através" destes. Os cardines são os pontos onde a Eclíptica intersecta os referidos círculos (Horizonte e Meridiano). O Zodíaco faz, aparentemente, uma volta completa por dia (movimento primário ou, justamente, diurno). Se a Eclíptica coincidisse ou fosse paralela ao Equador Celeste, os signos "ascenderiam" e "descenderiam" segundo um ritmo constante. Mas como é inclinada em relação ao Equador Celeste (actualmente cerca de 23.5º), os signos ascendem (e descendem) com inclinações e velocidades diferentes, Os segmentos resultantes do cruzamento da Eclíptica com o Horizonte e com o Meridiano não são do mesmo tamanho (excepto nos dois equinócios). A divisão das 'Casas' (Loci), depende (nos métodos angulares) da prévia localização dos quatro pontos fundamentais mencionados. 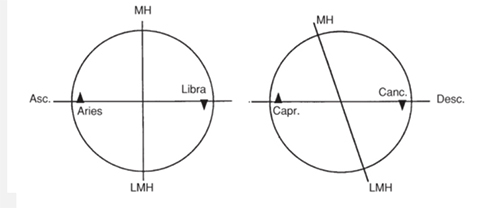 Oscilação do eixo MC-FC ("MH"-"LMH", Meio-Céu e Fundo-Céu (terminologia
actual). No esquema à esquerda (equinócio vernal), os quadrantes são
rigorosamente iguais (como serão no equinócio outonal) ; à direita,
verifica-se assimetria na sua dimensão (Beck, R., A Brief History of Ancient Astrology,
Blackwell Publishing, 2007, p.32). Os dois eixos só são perpendiculares
quendo os equinócios são coincidentes com a linha de horizonte: "Géminus
(Isagoge, 5) explique comme quoi le méridien ne divise en parties
égales que le tétragone contenant les solstices et équinoxes, au moment
où les équinoxes coïncident avec la ligne d'horizon. Pour toute autre
position, le Zodiaque est divisé en quadrants inégaux, la différence
pouvant aller du simple au double (quadrants de 60 à 120 degrés)." (Bouché-Leclercq, Op. cit., p.259, n.2)
Seguimos doravante uma breve exposição (Quanto tempo gasta um signo em nascer, & em se por & e com quantas partes da equinocial nasça, & se ponha...) do "Reportorio dos Tempos..." (1603) do mathematico Manoel de Figueiredo. O tratadista explica (Cap. 16) que o movimento da equinocial [Equador] é regular e uniforme: "em tempos iguais nascem & se põe arcos e partes iguais, segundo o movimento do Primum Mobile [movimento diurno]. O movimento do Zodíaco é desigual, pois não é executado sobre os seus pólos [os pólos da Eclíptica] mas sobre os 'Pólos do Mundo' [i.e. da Esfera Celeste]". Como se trata de círculos máximos, há sempre 6 signos sobre qualquer horizonte e 6 abaixo dele: "Nascer um signo rectamente se diz quando nasce com mor parte da equinocial que o seu arco, ou tamanho, & nascer "obliquamente" se diz quando nasce com menor parte da equinocial do que he o seu arco." Deste modo, metade dos signos [de Capricornus a Gemini] sobem "rectamente" (são de "ascensão longa":uma vez que o seu ângulo com o horizonte é maior, precisam de mais tempo para subir) e descem "obliquamente", os restantes [de Cancer a Sagittarius] sobem "obliquamente" (são de ascensão rápida) e descem "rectamente". A metade do Zodíaco de Aries até Virgo faz sempre menor ângulo com o horizonte do que a equinocial; a metade de Libra a Pisces faz sempre maior ângulo com o horizonte do que a equinocial. - Os signos no arco de Cancer a Sagittarius (Verão e Outono) são de ascensão longa ou recta, porque demoram mais tempo a erguer-se e os signos de Capricornus a Gemini (Inverno e Primavera) são de ascensão rápida ou oblíqua. N.B.: Repetimos que por "signos" se consideram os doze sectores (de 30º cada), contados em longitude na Eclíptica, tendo como referente, o Ponto Vernal. Figueiredo refere-se pois ao Zodíaco Tropical, baseado nos Equinócios e Solstícios, e não a um zodíaco Sideral, 'fenomenal', que representa efectivamente as posições dos asterismos. O desfasamento histórico entre ambos deve-se à Precessão do Equinócios (traduzida num lento movimento circular do eixo de rotação da Terra, como se de um pião se tratasse).  Ilustração da diferença dos horizontes (recto e oblíquo) relativamente à equinocial e à faixa zodiacal (Tractado da Spera... tirada de latim em linguage[m]..., Lisboa: Germam Galhard[e], ca. 1516) Portanto, diz-se que um signo nasce "rectamente" quando nasce com uma parte maior da equinocial do que o seu arco (=30º); nasce "obliquamente" quando em simultâneo se eleva uma parte da equinocial mais pequena do que o seu arco. Uma vez que o horizonte corta o zodíaco (em rigor: a eclíptica) em duas partes iguais, e sendo ambos círculos máximos, metade do zodíaco estará sempre acima do horizonte. Quando um ponto do zodíaco nasce, o seu oposto põe-se. Infere-se que a metade do zodíaco entre Aries e Virgo faz sempre um ângulo menor com o horizonte do que aquele que é feito pela equinocial. Inversamente, a metade entre Libra e Pisces faz um ângulo maior. No primeiro caso, nasce uma porção menor da equinocial; no segundo uma porção maior (relativamente ao arco do signo que ascende). Na esfera oblíqua, as duas metades do zodíaco igualam-se sempre em ascensões e descensóes. Se algum signo nasce com (i.e. em simultâneo) muitos graus da equinocial, o seu oposto nascerá com poucos. E o mesmo se entenderá no ocaso. Verifica-se, obviamente, uma simetria em relação aos pontos equinociais: "Regra he que quaesquer dous arcos eguaes e apartantes egualmente de quaesquer dos puntos equinociaes tem eguaes ascendimentos" (Tractado da Spera... tirada de latim em linguage[m]..., (Lisboa: Germam Galhard[e], [ca. 1516]). Resumo: como a latitude geográfica determina a relação entre Horizonte, Eclíptica e Equador Celeste, os diferentes signos demoram mais ou menos tempo (i.e. diferentes quantidades de ascensão recta) a "subir" sobre o horizonte. Trata-se, na prática, da porção do Equador Celeste que atravessa o meridiano enquanto um determinado signo, na sua totalidade, se eleva sobre o horizonte ("ascende") nessa latitude. Sob a linha equinocial (latitude = 0º), os tempos ascensionais são equivalentes às ascensões rectas (trata-se da própria definição de ascensão recta). As partes mais oblíquas do Zodíaco são aquelas que se elevam mais rapidamente acima do horizonte. Ao pôr-do-sol, com a posição invertida, aquelas que se elevaram mais rapidamente são as que descem mais lentamente. N.B.: É grave quando os historiadores (como testemunhamos amiudadamente) desconhecem ou baralham os conceitos e técnicas inerentes ou denotam graves lacunas nas indispensáveis competências astronómicas, e.g., confundindo o Medium Caeli com o Zénite (!), não compreendendo a dinâmica das chamadas Horas Sazonais ou convencionando que os signos se elevam e declinam em exactamente duas horas cada, independentemente da latitude do lugar e da obiquidade da Eclíptica. Esta animação
permite exemplificar as diferentes inclinações que a Eclíptica (linha graduada, cor de
laranja) assume relativamente ao horizonte local, bem como os diferentes azimutes nos quais o intersecta. A linha
branca "estática" é o
Equador Celeste. As constelações (siderais) elevam-se sucessivamente no nascente
(cada captura
incrementa aqui 2 horas). Onde ambos os círculos (Eclíptica e Equador)
se intersectam, situam-se os chamados pontos Aries e Libra
(que assinalam os dois equinócios e já não se encontram há muitos
séculos nas constelações "originais"). Utilizou-se como exemplo um dia do mês de Março,
elevação do pólo (latitude) de 40º N; Epoch actual. (SkyMap Pro)
Ascensão Recta, Ascensão Oblíqua e Diferença Ascensional
Os "Climas"
As 5 zonas climáticas originais num manuscrito, do séc. XII, do Somnium Scipionis de Macrobius; Os geógrafos da Renascença representavam habitualmente nove zonas. À direita, exemplo da Cosmographia
de Petrus Apianus, publicada pela primeira vez em 1524. Tal como a
utilização do Norte no topo dos nossos mapas é convencional, não se
tendo ainda estabelecido definitivamente no séc. XVI, também se
utilizavam amiudadamente os paralelos dos climas em detrimento dos
paralelos específicos de latitude.)
Aristóteles dividiu a Terra em cinco zonas, assumindo duas frígidas em redor dos pólos, uma inabitável zona tórrida centrada no Equador e duas zonas temperadas intercaladas (Meteorologica, II.5). Os "climas" (Gr. κλίμα, klima [pl. κλίματα, klimata], "inclinação" ou "declive" [de um ponto geográfico em relação ao Sol, à Eclíptica]) da Astronomia (e Geografia) clássica e helenística, eram divisões da Terra em faixas paralelas de latitude, i.e. justamente limitadas por círculos paralelos e conhecidas pelo nome de cidades conspícuas ou representativas (Meroé, Siena, Alexandria, Atenas, Babilónia, Rodes, etc.). Trata-se de um conceito astronómico e geométrico. O esquema (que mudou em função das épocas e autores) parece ter uma origem remota em métodos babilónicos (O. Neugebauer, HAMA, 725 et seq.), com a relacionação do comprimento do dia artificial (em oposição à noite) com o momento em que "subiam" graus consecutivos da Eclíptica, Segundo Paul Kunitzsch, talvez tenha sido Eratóstenes o primeiro a utilizá-lo. (La table des climats dans le corpus des plus anciens textes latins sur !'astrolabe, in: Science antique, Science medievale (Autour d'Avranches 235). Actes du Colloque International (Mont-Saint-Michel, 4-7 septembre 1998), ed. L. Callebat et 0. Desbordes, Olms-Weidmann, 2000, p.393). A divisão ptolomaica septenária tornar-se-á, de certo modo, canónica. O sábio alexandrino escalonou os climas em função do tamanho período de luz do mais longo dia do ano (i.e. Solstício de Verão). Cada um destes é definido como uma latitude que difere, das regiões adjacentes, um determinado intervalo no tamanho do maior dia do ano (o paralelo intermédio dos 7 climas tradicionais corresponde, aproximadamente, às latitudes (Norte): 16°, 24°, 30°, 36°, 41°, 45° e 48°). Em horas equinociais, no 1º "clima" o dia mais longo era de 12 horas; no 2º equivalia a 12h30, e assim sucessivamente. Não existindo ainda a latitude dividida em graus, utilizou-se a relação (proporcional) do comprimento das sombras gnomónicas equinociais dos diferentes locais da ecúmena (v. infra). 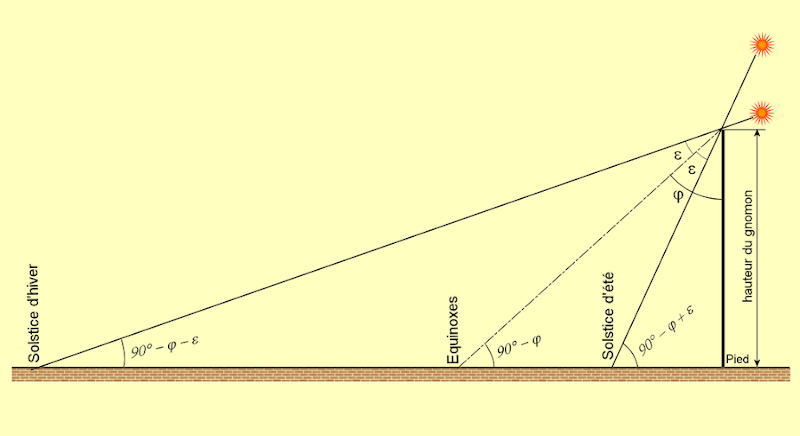 Latitude e relação gnomónica na projecção meridiana (Aubry Gérard)
Ptolomeu adoptou um sistema de 7 "climas" (Almagesto 2.12) que foi adoptado no período helenístico inicial e se tornou usual no contexto medieval e na geografia do mundo Islâmico (e.g., al-Biruni, al-Idrisi). O esquema funciona de modo a que a duração de horas diurnas no dia mais longo do ano (Solstício de Verão no Hemisfério Norte) incremente em intervalos de 1/4 de hora, desde 12 horas (no Equador) até 18 horas no paralelo equivalente a 58º. Depois, em passos maiores, até 24 horas no Árctico. É um procedimento com óbvia raíz astronómica. Para utilização nas suas tabelas geográficas, reduz a sua lista de quase quatro dezenas de paralelos a apenas 11, 7 ou mesmo 5 (no Phaseis, Opera II, 4,3-20). O conceito desapareceu mas a terminologia permaneceu até hoje, todavia referindo-se à predominância das condições meteorológicas regionais. O Ângulo Horário
Astronomia e Navegação: utilização do chamado "Bastão de Jacob" para medições angulares entre dois objectos (Jacques de Vaulx, Les
premieres Oeuvres de Jacques de Vaulx Pilote pour le Roy en la Marine
Contenantz Plusieurs Reigles Praticques Segrez Et Enseignementz très
necessaires pour bien et seurement naviguer par le monde..., 1584)
O AH de um ponto é definido como o ângulo entre dois planos: o plano do meridiano local, formado pelo eixo da Terra e o zénite; e outro contendo o eixo da Terra e o ponto propriamente dito (ilustração seguinte representa o ângulo horário do Sol, in: Chartrand, M. R., Amateur Astronomy Pocket Skyguide, Newnes Books, 1984) 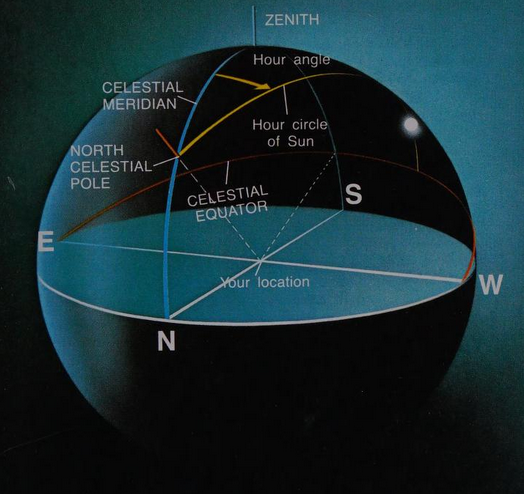 Por muitos séculos, os astrónomos definiram o 'tempo solar' como sendo o Ângulo Horário do Sol. Uma vez que este é zero ao meio-dia, os astrónomos mediam o dia a partir daí. Já referimos anteriormente um sistema de que recorre à Altitude e ao Azimute. Todavia, ambas as coordenadas se alteram com o tempo e a localização do observador, podendo somente ser utilizadas para identificar um objecto no céu num determinado momento específico. Existe um outro sistema que utiliza a Declinação e o Ângulo Horário. Este tem a vantagem de uma das coordenadas (a Declinação) ser "fixa", baseada no plano do Equador Celeste, i.e. independente do local do observador. A direcção de referência é obtida através de uma linha do plano do Equador que simultaneamente atravessa o primeiro meridiano. Este meridiano é específico para cada observador, sendo o círculo máximo que passa pelos pólos e pelo zénite. [N.B.; este meridiano existe nas circunstâncias específicas, local/hora; não confundir com a referência global: o Meridiano de Greenwich, origem da medição da Longitude.] O ângulo pode teoricamente ser medido em graus ou em tempo. É negativo a Leste do plano do meridiano e positivo a Oeste, ou simplesmente medido na direcção Oeste de 0h a 24h (360º equivale exactamente a 24h). O ângulo horário, emparelhado com a declinação, permite definir a localização exacta de um objecto. Como Chris Kitchin explica (Telescopes and Techniques: an Introduction to Practical Astronomy (2nd ed.), (Patrick Moore’s Practical Astronomy Series), Springer, 2003, Section 2), o Ângulo Horário (AH, HA em Inglês) de um objecto deve ser medido exclusivamente para Oeste a partir do Primeiro Meridiano (v. definição supra) em vez de na direcção Leste ou Oeste relativamente ao Meridiano de Greenwich. Em segundo lugar, a medida angular utiliza horas, minutos e segundos de tempo e não graus, minutos e segundos de arco. O valor do AH altera-se gradualmente, incrementando uniformemente com a passagem do tempo, enquanto o céu evolui no seu movimento diurno aparente. O AH de um objecto (corpo celeste) equivale a 0h00 quando esse objecto cruza o meridiano. Repare-se que existe uma relação directa com o Tempo Sideral: se, por exemplo, o AH de um objecto é de 3 horas, significa que a sua passagem meridiana aconteceu há 3 horas siderais. Em navegação astronómica, reconhece-se a posição de uma estrela pela sua "longitude" ao longo do Equador Celeste, medida para Oeste em graus (0º a 360º) a partir do primeiro ponto de Aries. Este ângulo é chamado Ângulo Horário Sideral (SHA no acrón. em Inglês). Em astronomia mede-se na direcção inversa (a partir do mesmo ponto), utilizando horas, minutos e segundos de tempo (v. Evans, David Stanley, Astronomy: An Introductory Guide, The English Universities Press, 1970 (1952)). 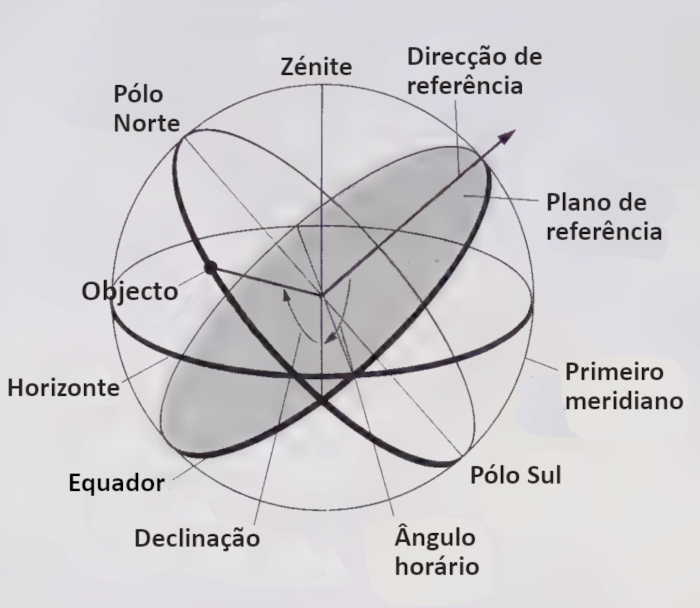 Declinação e Ângulo Horário (Kitchin, C., Telescopes and Techniques, fig. 4.12; ed. e trad. nossa) Com este enfoque geográfico, a relação entre os ângulos horários de dois objectos (1 e 2) pode ser exposta do seguinte modo:
AH2 = AH1 - ΔLongitude_Oeste ou... AH2 = AH1 + ΔLongitude_Este Δ = diferença; a Longitude é a diferença para o Meridiano de Greenwich. Esta relação diz respeito ao AH em diferentes locais de observação, e.g., se um objecto tem AH = 1h a partir de um determinado local, estará nesse instante a cruzar o meridiano num segundo local geograficamente afastado 15º (1h) para Oeste do primeiro. Na relação com a Ascensão Recta (α, que é uma coordenada "absoluta", independente das circunstâncias locais) e com o Tempo Sideral Local (TSL; LST em Inglês), o Ângulo Horário Local (AHL; LHA em Inglês) de um objecto será: AHL = TSL - α do objecto Na relação com o Tempo Sideral do meridiano universal, i.e. Greenwich (TSG; GST em Inglês) e com a Longitude (λ), teremos: AHL do objecto = TSG + λ do observador α = Ascensão Recta; λ = Longitude do observador (positiva para Leste de Greenwich, negativa para oeste); TSG = Tempo Sideral de Greenwich; TSL = Tempo Sideral Local N.B.: Quando uma estrela transita, i.e.,
quando se encontra no plano do meridiano, então o seu ângulo horário é
zero e o Tempo Sideral Local nesse instante equivale à Ascensão Recta
dessa estrela. - "Ponto Geográfico" de um objecto (corpo) celeste é o ponto na superfície da Terra do qual o objecto se observa no zénite em
determinado momento. A latitude desse ponto é equivalente à declinação
do objecto celeste. A sua longitude equivale ao Ângulo Horário de
Greenwich (GHA, em Inglês) desse objecto, se menor de 180º, ou 360º menos o Ângulo
Horário, se exceder. No primeiro caso a longitude é Oeste, no segundo é
Este. (Baker, R. H., Introduction to Astronomy (3rd ed.), D. Van Nostrand Company, 1947, p.65). Na
navegação astronómica, a convenção determina medir o ângulo para Oeste a partir do
Meridiano de Greenwich (ângulo horário de Greenwich, "Greenwich Hour Angle", GHA), do Meridiano Local (ângulo horário local, "local hour
angle", LHA) ou do primeiro ponto de Aries, "Sidereal Hour Angle", SHA.
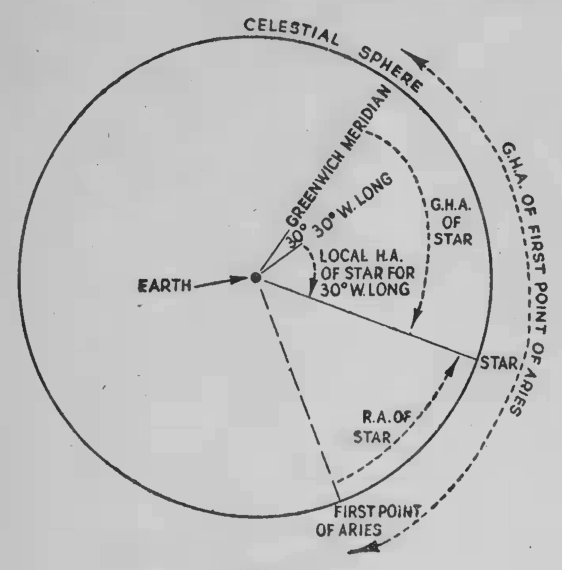 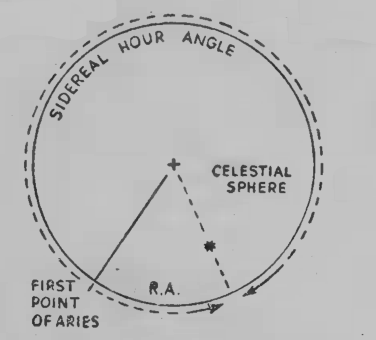 Principais
ângulos de uma estrela ("STAR"), medidos na Esfera Celeste (imaginando
que vemos a esfera "de cima" e "de fora", na perpendicular ao pólo);
também se assinala o Ângulo Horário de Greenwich do primeiro ponto de Aries; o observador neste exemplo situa-se na longitude 30º Oeste. À direita, relação entre a Ascensão Recta ("R.A.") e o Ângulo Horário Sideral ("Sidereal Hour Angle"); (esquemas de David S. Evans)
Complementamos com resumo de David S. Evans (Astronomy : an introductory guide,
The English Universities Press, 1970 (1952), pp.19-22), Utilizando uma
determinada estrela e alguns conceitos já expostos, temos:
Ângulo Horário de uma estrela = Ângulo Horário do ponto Aries + Ângulo Horário Sideral da estrela ou = Ângulo Horário do ponto Aries — Ascensão Recta da estrela. Ângulo Horário Local da estrela = Ângulo Horário de Greenwich da estrela — longitude Oeste. Ângulo Horário Local da estrela = Ângulo Horário de Greenwich do ponto Aries + Ângulo Horário Sideral da estrela — longitude do observador ou Ângulo Horário Local da estrela = Ângulo Horário de Greenwich do ponto Aries — Ascensão Recta da estrela — longitude Oeste do observador. (N.B: como já vimos acima, a longitude Leste conta como negativa e deve ser somada; o resultado deve situar-se entre Oº e 360º (24h); caso não aconteça, deve-se somar ou subtraír múltiplos para que se verifique.) - Nomograma para a Latitude 40ºN (por H. Robert Mill) 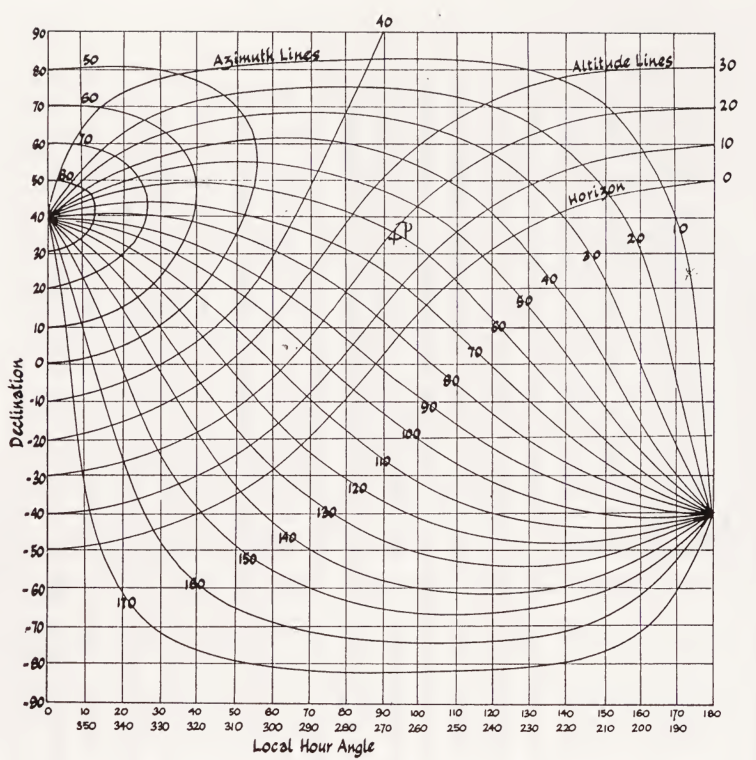 Situando
qualquer ponto através de dois dos parâmetros (Altitude, Azimute,
Declinação e Ângulo Horário Local ["LHA" em Ing.]), obtêm-se
imediatamente os restantes. Por exemplo: LHA e Dec. permitem saber Alt.
e Azim. (e vice-versa); Alt. e LHA permitem saber Dec. e Azim. (e
vice-versa); LHA e Azim. permitem saber Dec. e Alt. (e vice-versa).
Como exemplo, para o ponto P (desenhado no gráfico): LHA = 094º ou 266º, Alt. = 19º, Dec. = 34º e Azim. = 61º. - versão para imprimir (.PDF, 178KB) Outra solução analógica de H. R. Mills relaciona (com razoável aproximação) o TS, o LMT (Tempo Médio Local) e a data. [O LMT difere do solar aparente pois não tem em conta a Equação do Tempo, v. infra]. Qualquer um destes valores pode ser encontrado sabendo os outros dois, fazendo passar uma linha recta através das escalas. Na ilustração seguinte (que somente representa parte do nomograma) a linha demonstra que em 31 de Janeiro, quando o Tempo Sideral é aproximadamente 4h30m, o Tempo Local Médio é de 20h00. 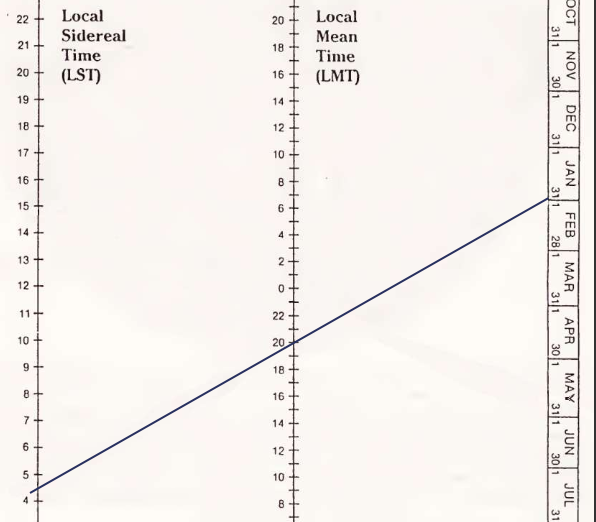 - versão para imprimir (.PDF, 34KB) O
Tempo Solar Médio (TSM) pode ser definido como o Ângulo Horário (AH) do
Sol acrescido de 12 horas. Estas horas extra fazem equivaler as 0h00 (referência) à
Meia-Noite. O sol "médio" é um corpo convencional (i.e.
imaginário) que se move tendo como referência o Equador (e não a
Eclíptica) a uma velocidade uniforme, percorrendo 360º em exactamente 1
ano. O TSM é pois uma medida uniforme também conhecida como "tempo
civil", o que usamos na vida quotidiana (excepto quando se fazem
ajustamentos como a chamada "Hora de Verão", etc.). O Tempo Solar
aparente ou verdadeiro, o do relógio de Sol, difere geralmente do TSM
devido a:
a) o Sol move-se percorrendo a Eclíptica (não o Equador);
A diferença entre o Tempo Solar verdadeiro e o TSM é a chamada Equação do Tempo. (Kitchin, Op. cit., pp.85-6)
(Δ = diferença) N.B. Nos almanaques, o Tempo Sideral de Greenwich (GST em Inglês) é tabelado para as 0h00.
A
curva da "Equação do Tempo" constitui a combinação dos efeitos das
curvas de dois componentes separados: a excentricidade da órbita e, por
outro lado, a obliquidade da Eclíptica. (H. N. Russell, R. S. Dugan and J. Q. Stewart, Astronomy: A Revision of Young's Manual of Astronomy, Ginn and Company, 1945 [1926], vol I, Fig. 65). Outro gráfico (Mills, H. Robert, Practical Astronomy... Op. cit.,
1994, p.95) onde se observa que a combinação das duas curvas: a que representa a componente da excentricidade da órbita
terrestre e a que representa a inclinação da Eclíptica.
Na Astronomia do passado, a chamada "Equação do centro" era o excesso de longitude do Sol, relativamente à que este teria se o seu percurso aparente fosse uniforme. A Equação do Tempo é também uma descrição das características horizontais do analema da Terra (v. infra), uma curva em forma de '8' assimétrico que representa graficamente a posição do Sol no céu à mesma hora em cada dia do ano.
A Equação do Tempo
é o nome dado à quantidade que deve ser acrescentada (ou subtraída) ao
"tempo médio" (ou legal, do relógio) para obter o "tempo aparente", o
dos fenómenos, i.e. do relógio de Sol. É a diferença entre o Tempo Médio e o Tempo Aparente,
No passado, "equação" significava algo a ser acrescentado para alcançar
uma equivalência. A curva do gráfico mostra os valores do Tempo Aparente ao longo do ano. (Muirden, J., Astronomy Handbook,
Arco Publishing, Inc./ Kingfisher Books, Limited, 1982, p.33)
Como exemplo, para conhecermos o Meio-Dia verdadeiro, astronómico, num determinado local geográfico a oeste do meridiano de Greenwich (e.g., em Portugal) para determinada data, precisamos acrescentar (às 12h00) 4 minutos por cada grau de longitude a oeste do meridiano de referência, que é o de Greenwich (acautelando mais 1 hora caso vigore a chamada Hora de Verão, UT+1) e depois, em função do dia específico do calendário, acrescentar ou subtrair os minutos indicados na tabela da Equação do Tempo (nas datas situadas na zona a verde (na figura acima) adicionamos, pois o Sol está "atrasado"; nas da região a castanho subtraímos pois o Sol está "adiantado"). O Analema é a figura com com a forma de "8" trilhada pelo Sol se visto de um local específico ao longo do ano, à mesma hora. Se todos os dias registarmos uma captação do Sol à mesma hora e com uma câmara apontada na mesma direcção, obteremos uma foto compósita como a que segue (fonte: Dennis di Cicco/Sky & Telescope).
A
inclinação do eixo terreste relativamente ao plano da sua órbita
determina, como sabemos, o aparente movimento ascendente e descendente
do Sol ao longo do ano. O analema mede duas vezes esse ângulo (47º, na
vertical). O movimento lateral aparente é devido ao acumular, dia após
dia, da diferença de alguns segundos a que se assiste no seu movimento
aparente para Leste. No analema, o Sol está no ponto mais baixo em 21
de dezembro. "Move-se" no sentido ascendente até 21 de junho e volta a
"descer" essa curva até voltar ao primeiro ponto. Passou um ano.
O analema é a representação gráfica da Equação do Tempo, que mede a diferença entre a Ascensão Recta do Sol médio e a Ascensão Recta do Sol verdadeiro, num determinado instante. (Vallières, J., Devenez astronome amateur, Québec Science Éditeur, 1980, p. 60)
- Relógios de Sol (tipologias principais): 1) Os "Equatoriais", que possuem um gnómon ou estilete paralelo ao eixo da Terra, em torno do qual o Sol parece rodar 15º por hora; 2) Os que se baseia na Altura (Altitude) do Sol sobre o horizonte; 3) Os que dependem do azimute do Sol, ou os conhecidos como "analemáticos". Possuem geralmente um estilete vertical adaptável à declinação solar. Tempo Universal e Tempo Universal Coordenado O Tempo Universal (UT, Universal Time) equivale, na prática, ao antigo GMT (Tempo Médio de Greenwich), O Tempo Universal Coordenado é uma escala de tempo que acrecenta as qualidades de precisão do Tempo Atómico Internacional (International Atomic Time, IAT; TAI em Português). É pois designado com o modificador "Coordenado" pois, eventualmente, é ajustado (devido às oscilações da duração da órbita da Terra, i.e. movimentos dos pólos e variações sazonais da rotação) ao TAI, quando se afasta deste mais do que 0.9s. Somente relevante quando estão em causa fracções se segundo. De outro modo, equivale ao GMT. Períodos Planetários O
tempo que um planeta demora a percorrer a sua órbita uma vez (período
orbital) é habitualmente chamado o "período sideral" do planeta, uma
variável fundamental. Todavia, a nossa observação dos planetas é feita
a partir da Terra, que está em movimento. Logo, não observamos o
período sideral directamente mas sim o período requerido pelo planeta
para voltar à mesma posição relativamente à Terra e ao Sol. O intervalo
entre dois retornos sucessivos à mesma posição relativa (e.g., entre suas oposições) é o chamado "período sinódico" desse planeta.
- Relação entre ambos os períodos: VAR = 360/T - 360/P = 360/S VAR - Velocidade Angular Relativa T - período sideral da Terra (= 1 ano) P - período sideral do planeta S - período sinódico do planeta (360 pois a circunferência perfaz 360 graus) Utilizando o ano (T = 1) como unidade, temos para um planeta exterior: P = S / S - 1 e para um planeta interior: P = S / S + 1 Medição da Longitude de uma Estrela (na Época Helenística)
A referência é o Ponto Vernal (ou primeiro ponto de Aries). Se se conseguísse medir a distância angular entre o Sol e uma estrela situada na Eclíptica,
determinava-se directamente a longitude desta. Mas nunca se consegue
observar ambos os astros em simultâneo (devido ao brilho solar). Foram
gizados dois métodos e ambos utilizavam a Lua. O de Hiparco utilizava
os eclipses lunares. O de Ptolomeu (explicado no Almagesto) funcionava a dois momentos, sendo demonstrado na seguinte ilustração.
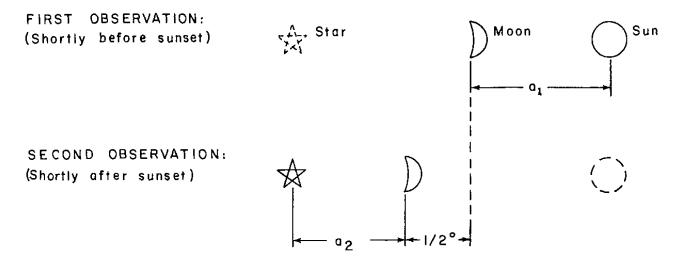 Pouco
antes do ocaso, media-se o arco de longitude entre a Lua e o Sol (neste
momento a estrela ainda seria invisível devido ao brilho solar). Um
pouco mais tarde, avançando o crepúsculo e estando a estrela visível,
media-se o arco longitudinal entre esta e a Lua.
Ou seja: Longitude da estrela = longitude do Sol + Arco de longitude entre o Sol e a Lua + Arco de longitude entre a estrela e a Lua + correcção O primeiro termo era conhecido e consultado numa tabela ("lugar do Sol" para a data específica), o segundo e terceiro resultam da observação com uma esfera armilar com componentes para visada. O último, a correcção, é mais complexo. Tem em conta dois detalhes: o movimento da Lua para leste ao longo da eclíptica (circa 12º por dia, 1/2º numa hora) e a sua paralaxe (diferença entre ambas as observações), utilizando a trigonometria. A partir da medição de uma estrela pivotal, extrapolava-se para outras estrelas, pois distâncias angulares entre estas são "fixas". (Ilustração e explanação completa em Evans, J., The History and Practice of Ancient Astronomy, Oxford University Press, 1998, p.250 et seq.). "sozein ta phainomena" (σῴζειν τὰ φαινόμενα): "salvar" ou "preservar" os fenómenos Quanto
à Terra, o nosso sustento, a qual roda em torno do eixo que atravessa o
universo, foi estabelecida como guardiã e produtora da noite e do dia;
ela que é a primeira e a mais velha das divindades geradas dentro do
céu. Explicar as danças destes astros e as confluências que mantêm uns
com os outros, os recuos e os avanços dos seus círculos, uns em relação
aos outros, quais são os deuses que se encontram em conjunção e quantos
estão opostos uns aos outros, e ainda quais se colocam uns diante dos
outros e durante quanto tempo se escondem de nós para tornarem a
aparecer, e enviam maus presságios e sinais de eventos que hão-de
acontecer àqueles que não conseguem entendê-los à luz da razão, sem ter
diante dos olhos uma imitação destes fenómenos [...]. (Timeu, 40c)
Segundo Rudolfo Lopes (ed., trad,), "ao começar a descrever os atributos do objecto em estudo, Timeu dá-se conta de que o mundo pertence à ordem do devir, pois apresenta todas as características do sensível: é visível (oratos: 28b7), tangível (aptos: 28b7) e tem corpo (sôma echôn: 28b7). Ora, se o mundo é deveniente, como produzir um discurso verdadeiro e estável sobre ele? É da resposta a esta pergunta que depende a validade de toda a proposta cosmológica." (Timeu-Crítias, Tradução do grego, introdução, notas e índices), Centro de Estudos Clássicos e Humanísticos - Universidade de Coimbra, 2011, p.33) A questão sobre como acautelar os phainomena resulta da perplexidade de Platão, no Timeu, com a “dança dos astros”, as regularidades e, consequentemente, as irregularidades
incompatíveis com a natureza circular e uniforme da idealização
expendida. Platão menciona que para podermos investigar os fenómenos “à
luz da razão”, faz-se necessário ter contacto com a “imitação destes
fenómenos”. Aqui surge pela primeira vez a noção de phainomena como chave para a interpretação. Da procura de soluções resultam as soluções ulteriormente desenvolvidas, a partir de Eudoxo. A Esfera Armilar “O
ceo consta de muitos corpos conjuntos, como tratamos no nosso liu. da
Sphaera, que se fora hum corpo, contradezia a todo o natural poderse
nelle fazer tantos, & tão diversos mouimentos como parecem; &
aísi pella investigação dos mouimentos diversos, & corpos lúcidos,
se alcãçou o numero dos ceos. Em tempo de Aristoteles, se consideraram
somente oito; Hyparco, & Ptolemeo, acharão ser noue; el Rey Dom
Affonso por muitas investigações, & experiencias alcançou serem
dez; afora o Empyreo que poem os Theologos, don de he o lugar &
morada dos bemauenturados, pois a ordem e sitio que tem hũs com outros
he na forma seguinte.” (segue-se gravura c/ ilustração convencional das
esferas concêntricas)
(André do Avelar, Chronographia ou reportorio dos tempos: o mais copioso que te agora sayo a luz conforme a nova reformação do Santo Padre Gregorio XIII, Nesta quarta impressam reformado, accrescentado pello mesmo author (Impresso em Lisboa: por Jorge Rodriguez a custa de Estevão Lopez mercador de livros, 1602), p.161)
A
Esfera Armilar pode ser descrita como um "esqueleto" da Esfera Celeste
ou um "Modelo do Universo". Algumas fontes recuam a sua origem a
Anaximandro de Mileto (séc. VI a.C.). Hiparco (c.190–120 a.C.)
reconhece Eratóstenes (276–194 a.C.) como o seu criador. Intimamente
relacionadas e confundidas com os globos, quase não há vestígios de
exemplares antigos ou medievais. Segundo Mercè Comes (Alfonso X's Armillary Sphere
[XXII International Congress on the History of Science, Beijing,
2005]), Ptolomeu descreveu no Almagesto um instrumento chamado astrolabon, composto por sete anéis e utilizado para observar os objectos celestes, principalmente as estrelas.
Estrutura do astrolabon: Na igualmente influente Geographia (gr. Γεωγραφικὴ Ὑφήγησι), o sábio alexandrino mencionou outro equipamento semelhante, o meteoroscópio, com mais dois anéis (um para o Equador e outro azimutal), vocacionado para a resolução de problemas de Geografia e Astronomia Esférica. Ptolomeu utilizou coordenadas eclípticas. Encontramos
comentários e paráfrases das descrições observacionais de Ptolomeu em
autores como Pappus (séc. IV AD) e Proclus (c.412-485). Teão (Θέων) de Alexandria (séc. V), um dos comentadores
do Almagesto, descreveu de modo detalhado a instrumentação ptolomaica.
Mais tarde, surge no contexto Islâmico um terceiro instrumento que era uma
combinação dos anteriores. Em Árabe, uma esfera armilar é designada Dhāt al-ḥalaq. A esfera armilar descrita no ‘Libro de las Armellas’ de Alfonso X (meados do séc. XIII), que pertence aos Libros del Saber de Astronomía,
é baseada em tratados árabes, por seu lado respaldados em Ptolomeu. De
facto, As esferas ibéricas do séc. XII podem (como referido pelos
editores da Enciclopedia Britannica, consultada em linha),
ter sido os protótipos de todas as ulteriores esferas construídas na
Europa ao longo dos séculos seguintes. No séc. XVI, Tycho Brahe
construirá diversas, tanto nas configurações eclípticas como equatoriais. Todavia, as práticas observacionais evoluiram rapidamente e em breve a esfera armilar se tornaria obsoleta.
Na antiga
China foi supostamente independentemente inventada por Luoxia Hong (séc. I a.C.) e
desenvolveu-se durante a dinastia Han (Sun, X. (2015). Chinese Armillary Spheres. In: Ruggles, C. (eds.) Handbook of Archaeoastronomy and Ethnoastronomy. Springer). Os instrumentos extremo-orientais eram equatoriais e não eclípticos, e incluiam tubos de visada em vez de anéis ou alidades com "pontarias" (vide introdução do cit. paper de Mercè Comes,
2005). Aí assumiram uma função predominantemente demonstrativa, daí
por vezes o recurso documentado a um mecanismo de rotação automática
(e.g., o equipamento movido pela força da água desenhado por Su Sung no
séc. XI), As tradições Ocidentais e Chinesa convergiram no séc. XVII
com a chegada dos Jesuítas ao Império do Meio.
A esfera armilar também foi utilizada na Índia desde cedo. Chamada Golabandha ou Gola-yantra ("instrumento esférico"). É mencionada nos tratados de Āryabhata (476 A.D.). Entre outros citáveis, o Goladīpikā é um tratado detalhado acerca dos globos e da esfera armilar, coligido entre 1380 e 1460 por Parameśvara (K. V. Sarma (2008), Armillary Spheres in India; in: Selin, H. (ed.) Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer, Dordrecht).
O
sextante é o epítome do instrumento náutico. O seu principal uso é
medir o ângulo entre um objeto astronómico e o horizonte para fins de
navegação astronómica. Utiliza
um sistema de dupla reflexão. Na prática, faz-se uma visada simultânea
de modo a conseguir a chamada "coincidência aparente"(e.g. entre o Sol e o horizonte visivel).
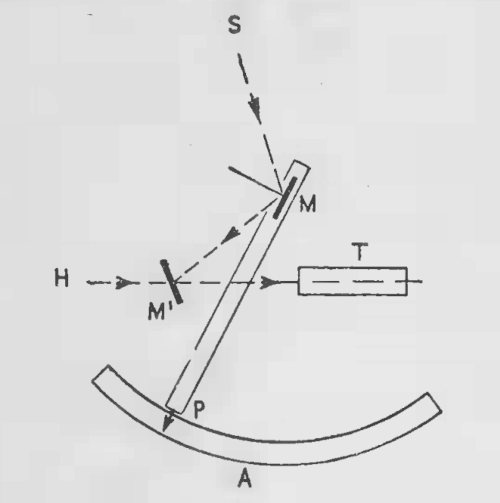 Esquema do funcionamento do sextante (D. S. Evans)
O princípio do sextante está simplificadamente ilustrado no esquema supra (David S. Evans, Op. cit., Fig.4). M e M'
são dois espelhos planos, o primeiro fixado na estrutura do instrumento
enquanto o segundo (o espelho "do horizonte") está montado num braço
rotativo que permite o movimento do ponteiro P sobre o arco graduado A. T
é um pequeno telescópio através do qual o operador ou utilizador faz a
visada. Quando o faz, observa duas imagens: uma é a do Horizonte, que
chega ao telescópio seguindo o percurso luminoso horizontal H, atravessando o espelho M' (este espelho especial
tanto reflecte como permite que a luz o atravesse). Simultaneamente, o
utilizador observa a imagem do astro, cuja luz segue o caminho S, é reflectida em M, depois em M' para finalmente entrar no telescópio T. Isto acontece apenas quando quando M está no ângulo correcto em relação ao astro medido. Como P se move ao longo do arco A,
em determinado momento o astro será observado no campo de visão
exactamente alinhado com a linha do Horizonte. Lê-se então a medida na
graduação inscrita no arco A.
Como se sabe, segundo a Óptica, inclinar um espelho segundo um determinado ângulo determina que ele reflicta um raio de luz segundo um ângulo que é o dobro do inicial. O sextante acautela esta característica e a sua escala já está graduada com separações de "meios-graus", permitindo ler directamente o resultado. Quando M e M' estão paralelos, o utilizador observa o Horizonte directamente através de M' e, em simultâneo, duplamente reflectido por M e o próprio M'. PM será então paralelo plano do espelho M' e a escala em A indicará 0º. O ponto zero e início da escala graduada fica aí, à direita na ilustração. Os sextantes incluem outros refinamentos, tais como escalas vernier para leituras ainda mais precisas ou filtragem no telescópio para proteger o utilizador quando "mede" o Sol. A altura do observador pode ser geralmente negligenciada mas não é o caso se observa de um ponto elevado ou em aviação. Nesses casos há uma correcção que deve ser subtraída ao resultado obtido na medição (v. Evans, D. S., Astronomy: an introductory guide, Op. cit., pp.6-7)  Orientação (rosa-dos-ventos, agulha, bússola) e designação, moderna e tradicional mediterrânica, dos ventos (Allain Manesson Mallet, Description de l'univers, contenant les différents systèmes du monde, les cartes générales..., Paris, 1683; Tome 1, Fig. LXV) [voltar] |
|||||||||